Descripción lagrangiana y descripción euleriana
2011-10-03
Las descripciones lagrangiana y euleriana son dos formas de ver la mecánica de medios continuos. La descripción lagrangiana consiste en hacer un seguimiento de las partículas materiales, mientras que la descripción euleriana consiste en medir lo que pasa en puntos fijos del espacio. Ambas descripciones son equivalentes y a veces una es más cómoda de usar que la otra.
En el último artículo introdujimos los conceptos de masa de control y volumen de control. Al estudiar una masa de control, estudiamos un fragmento del material y seguimos su movimiento. Al estudiar un volumen de control, estudiamos lo que atraviesa una parcela del espacio. El enfoque de las masas de control es el enfoque lagrangiano, mientras que el enfoque de los volúmenes de control es el euleriano. Estos enfoques sirven para todo. Por ejemplo, veamos cómo podemos estudiar los artículos que llevan los clientes de un supermercado:
- Descripción lagrangiana
- Podemos seguir a cada cliente. A cada uno le ponemos una etiqueta mental (su nombre, por ejemplo). De esta manera, podemos preguntarnos dónde está cierto cliente en un momento determinado y qué artículos lleva encima.
- Descripción euleriana
- Podemos quedarnos en lugares fijos del espacio, tales como las cajas. Estos lugares son fáciles de etiquetar e identificar en un plano del edificio. De esta manera, podemos preguntarnos, por ejemplo, qué artículos hay en la cinta transportadora de cierta caja.
Ambas descripciones son equivalentes.

La descripción lagrangiana adopta el punto de vista del material o,
en nuestro ejemplo, de los clientes del supermercado.

La descripción euleriana adopta el punto de vista del espacio fijo.
En nuestro ejemplo, puede ser lo que ve una videocámara colgada de la
pared.
Extendamos el anterior ejemplo a un caso general con un poquito de matemáticas.
Descripción lagrangiana
Supongamos que tenemos un conjunto de objetos materiales (como un continuo de puntos materiales o los clientes de un supermercado). A cada uno le asignamos una etiqueta mental. Esta etiqueta será la posición (en cierto instante de referencia) de cada objeto material, X0. A la posición del objeto X0 la llamaremos X(t,X0). Cada objeto material tendrá unas propiedades (tales como su temperatura o los artículos que porta en la cesta de la compra) que pueden variar con el tiempo t y que denotarmeos mediante el símbolo Cl(t,X0).
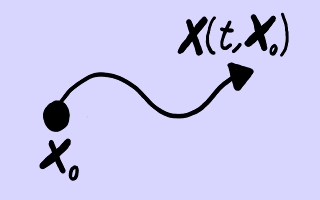
Trayectoria de una partícula como función de su posición inicial
y del tiempo.
Descripción euleriana
Ahora vamos a estudiar no los objetos materiales, sino los puntos x del espacio. Cada uno de estos puntos puede estar ocupado por un objeto material con ciertas propiedades y podemos describir, por lo tanto, las propiedades presentes en el punto del espacio x en el instante t mediante el símbolo Ce(t,x).
Relación entre ambas descripciones
Al menos de forma simbólica, podemos establecer
rápidamente de qué forma están relacionadas las descripciones
lagrangiana y euleriana. Supongamos que la partícula X0 ocupa en el
instante t la posición X(t,X0) = x.
Las propiedades de la partícula según la descripción lagrangiana
son las propiedades del punto según la descripción euleriana:
Cl(t,X0) = Ce(t,X(t,X0)).
De igual manera que la trayectoria de las partículas X(t,X0)
nos sirve como una aplicación que pasa del espacio de las etiquetas
asociadas a los puntos materiales (es decir, sus posiciones iniciales
X0) al espacio
de los propios puntos x,
podemos hacer la transformación inversa, al menos si no hay fenómenos
singulares tales como el colapso de dos partículas materiales y su
unión en una única partícula. Formalmente y con cierto abuso de
notación, podemos escribir esta transformación inversa así:
X−1(t,x) = X0.
De esta manera, establecemos la equivalencia entre las dos
descripciones:
Ce(t,x) = Cl(t,X−1(t,x)).
Las transformaciones directa e inversa, es decir, las trayectorias de las partículas en función del tiempo o las posiciones iniciales de las partículas en función de sus posiciones finales en cierto instante, no suelen ser conocidas de antemano, sino que suelen ser parte de la solución del problema.
Muchos modelos físicos son relativamente fáciles de plantear con una descripción y difíciles de plantear con la otra. Por ejemplo, los modelos de mecánica de fluidos suelen prestarse muy bien a la descripción euleriana, mientras que los de grandes deformaciones de cuerpos sólidos suelen ser más cómodos de tratar con una descripción lagrangiana.
Descripciones mixtas
A veces, sucede que resulta conveniente combinar la descripción lagrangiana y la descripción euleriana. Por ejemplo, si queremos estudiar la caída de la nieve, podemos diseñar un modelo matemático en el que los copos de nieve son pequeñas partículas puntuales a las que seguimos con una descripción lagrangiana, mientras que la parte gaseosa de la atmósfera es un gas continuo que estudiamos mediante una descripción euleriana. También sucede a menudo en problemas de interacción fluido-estructura que el medio fluido se deja atacar mediante una descripción euleriana y la estructura, en cambio, se resiste mucho menos a una descripción lagrangiana.
Categorías: Física, Matemáticas
Permalink: http://sgcg.es/articulos/2011/10/03/descripcion-lagrangiana-y-descripcion-euleriana/
