¿Nos mojamos menos cuando llueve si corremos? (3)
2012-02-02
En los anteriores artículos de esta serie (aquí está el primero y aquí está el segundo), elaboramos un sencillo modelo matemático que permite estimar lo mucho que se moja un individuo bajo la lluvia en las siguientes condiciones:
- la lluvia es uniforme y constante;
- la lluvia cae perpendicular a la dirección del movimiento (es decir, que no sólo puede caer verticalmente, sino que también puede tener cierta componente de lado);
- podemos modelar el individuo como un prisma;
- el camino recorrido por el individuo es rectilíneo y horizontal;
- el individuo recorre el camino a rapidez constante.
Bajo estas condiciones, vimos que el sujeto de
estudio se moja a través de su superficie frontal Af y de la superficie
perpendicular a la dirección de caída de la lluvia Ap. La lluvia tiene una
densidad equivalente ρ (que
es la masa total de agua contenida en la atmósfera que rodea
al individuo dividida por el volumen de dicha atmósfera) y cae
con una velocidad vp
(hemos cambiado ligeramente la notación). El individuo avanza
con rapidez u por el camino
de longitud l, de modo que
el tiempo total invertido en recorrer el camino es l ⁄ u.
El agua recibida a través de las superficies Ap y Af es una medida
de lo que ese empapa el individuo y sigue la ley M(u):
M(u) = ρ Ap l vp ⁄ u + ρ Af l.
El primer sumando es la contribución de la velocidad de caída
perpendicular al avance y el segundo término se debe al propio
desplazamiento y es igual a la masa de agua contenida en el volumen
barrido por el individuo al desplazarse. Si el individuo pudiera
moverse con rapidez infinita, vemos que se mojaría el mínimo posible
según este modelo, M(∞).
Podemos crear así el siguiente índice de empapamiento relativo:
M(u) ⁄ M(∞) = (Ap ⁄ Af) (vp ⁄ u) + 1.

Velocidad relativa de la lluvia. En esta figura, la lluvia
viene de espalda y avanza más rápido que el individuo, así que
moja por detrás.
Introduzcamos una complicación adicional: veamos lo que
pasa cuando la lluvia tiene una componente adicional vf en la dirección de avance
que tomaremos positiva hacia adelante y negativa hacia atrás.
La velocidad relativa de la lluvia en esta dirección es vf − u;
es positiva cuando el individuo corre menos que la lluvia (por lo
que se moja por la espalda) y es negativa cuando el individuo corre
más que la lluvia (por lo que se moja de frente). En todo caso,
la superficie mojada por esta componente tiene la misma magnitud,
Af, mientras que la
velocidad relativa del agua entrante tiene el valor absoluto |u − vf|,
de modo que la contribución frontal o trasera pasa a ser
ρ Af l |u − vf| ⁄ u
y el total M(u) queda así:
M(u) = ρ Ap l vp ⁄ u + ρ Af l |u − vf| ⁄ u.
Con un valor finito de la velocidad de avance vf de la lluvia, el agua
capturada M(∞) al correr
extremadamente rápido queda, como antes, igual a la masa de agua
contenida en el volumen barrido por el individuo al recorrer el
camino. Podemos expresar el índice adimensional M(u) ⁄ M(∞)
como hicimos antes:
(Ap ⁄ Af) (vp ⁄ u) + |u − vf| ⁄ u.
El primer sumando es la contribución de la componente
perpendicular (vertical y lateral) de la lluvia y el segundo sumando
es la contribución en la dirección del movimiento del individuo.
Cuando la lluvia viene de frente (es decir, cuando la componente
de avance vf de la lluvia
es negativa), el índice de empapamiento es monótono decreciente con
la velocidad de desplazamiento u
del individuo. Cuando la lluvia viene de espalda (cuando vf es positiva), en cambio,
la situación es mucho más interesante. El primer sumando, el de
la componente perpendicular, tiene el mismo comportamiento que antes,
pero el segundo sumando decrece al principio con la rapidez de avance
u, tiene un mínimo y a partir de
ahí se aproxima a un valor asintótico (la unidad). El mínimo no es
suave, sino que hay una discontinuidad en la pendiente, que pasa de
ser negativa a ser positiva bruscamente. Este mínimo se da cuando
el individuo avanza tan rápido como la lluvia (es decir, cuando
u = vf)
y, por lo tanto, no se moja ni por delante ni por detrás; la
contribución frontal se anula. Este punto de mínima contribución
frontal es también el mínimo del índice completo M(u) M(∞)
cuando se cumple la siguiente condición de que la pendiente de descenso
de la contribución perpendicular es menos importante que la pendiente
de ascenso de la contribución frontal en el punto u = vf:
(Ap ⁄ Af) (vp ⁄vf) ≤ 1.
Cuando se da la igualdad, la velocidad de avance de la lluvia
es crítica y el mínimo se extiende hasta el infinito y
el aumento del agua capturada de frente al correr más se compensa
exactamente con el descenso de la cantidad de agua capturada por
arriba y por el lado; cuando se da la desigualdad estricta, entonces
la velocidad de avance de la lluvia es supercrítica, el
mínimo es único y correr más implica mojarse más; finalmente,
cuando no se cumple la condición, entonces la velocidad de avance
de la lluvia es subcrítica, el índice de empapamiento
es monótomanente decreciente y siempre conviene correr más, pero
hay una pérdida de efectividad marginal cuando el agua empieza a
venir relativamente de frente y no por la espalda. Se aprecia,
además, que hay un intervalo de valores de la celeridad u para el que el individuo se moja menos
que cuando se desplaza extremadamente rápido:
1 ⁄ 2) [(Ap ⁄ Af) vp + vf] < u < ∞.
Fuera de este intervalo, el individuo se moja más que cuando
va extremadamente rápido (es decir, que cuando u → ∞). Este
intervalo sólo existe cuando existe el mínimo, es decir, cuando
se cumple la condición sobre las pendientes que vimos antes.
Las siguientes curvas ilustran los distintos casos que hemos visto.
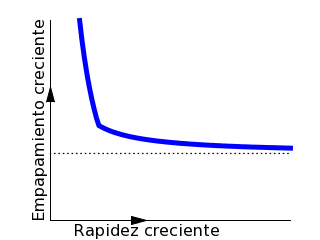
Curva de empapamiento cuando la lluvia viene despacio
de espalda (a velocidad subcrítica), de modo que no hay mínimo
finito, pero sí un quiebro en la pendiente. La línea de puntos
es el valor asintótico al que tiende la curva cuando la rapidez del
desplazamiento es muy elevada.
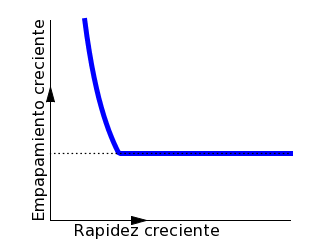
Curva de empapamiento cuando la lluvia viene de espalda a velocidad
crítica, tal que, a partir de cierto punto, los dos efectos de correr
más se anulan mutuamente.
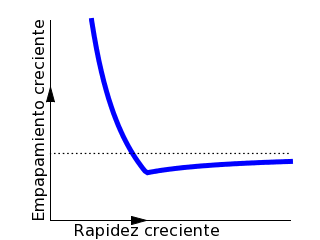
Curva de empapamiento cuando la lluvia viene deprisa de espalda
(a velocidad supercrítica), de modo que hay un intervalo semiinfinito
en el que conviene correr y una rapidez óptima, la de avance de
la lluvia, para la que el individuo se moja lo mínimo posible.
La línea de puntos es el valor asintótico al que tiende la curva
cuando la rapidez del desplazamiento es muy elevada.
De todo lo que hemos visto se deduce lo siguiente:
- si la lluvia viene de frente o sólo un poco de espalda, entonces conviene correr todo lo posible;
- si la lluvia viene con fuerza de espalda, entonces conviene correr tanto como la lluvia para que no pueda mojar ni por delante ni por detrás;
- si no es posible correr tanto como la lluvia, al menos conviene correr tanto como es posible;
- incluso cuando la lluvia viene de espalda con rabia, es más grave correr demasiado despacio que correr demasiado rápido.
Otros artículos de la serie
- Caso más sencillo: lluvia uniforme y constante que cae vertical y velocidad de avance también constante.
- Como el anterior caso, pero con lluvia con componente lateral.
Categorías: Matemáticas
Permalink: http://sgcg.es/articulos/2012/02/02/nos-mojamos-menos-cuando-llueve-si-corremos-3/
