SGCG

Volver arriba

Braquistócrona

2011-04-19

El problema de la braquistócrona es el de encontrar el camino más rápido entre dos puntos que puede seguir un cuerpo forzado a seguir dicho camino en presencia de un campo gravitatorio uniforme y constante y en ausencia de fricción. Este problema, propuesto por Johann Bernoulli a finales del siglo XVII, supuso un excelente estímulo para el desarrollo de las técnicas del cálculo infinitesimal y el cálculo de variaciones.

A muchos estudiantes se les habla del problema de la braquistócrona y se les revela cuál es la solución sin entrar en detalles sobre cómo llegar a ella. Este artículo está dedicado a esas mentes curiosas que tienen las herramientas adecuadas en sus manos para resolver el problema, pero carecen todavía de la soltura adecuada para hacer un buen uso de ellas y necesitan un empujoncito. El rigor a veces brillará un poco por su ausencia y la notación será objeto de abuso, pero espero que los incautos lectores más exigentes en el terreno matemático sean misericordes.

Planteamiento del problema

La física de este problema es clásica y no relativista: son de aplicación las leyes del movimiento de Newton y el principio de relatividad de Galileo, el espacio es tridimensional y euclídeo y el tiempo sirve de etiqueta independiente.

Tenemos un cuerpo puntual y con masa, sometido a la atracción de un campo gravitatorio uniforme e invariable en el tiempo. Sostenemos el cuerpo en el borde de una rampa que conecta con un punto de destino que se encuentra más abajo. En un momento dado, soltamos el cuerpo y dejamos que se deslize sin rozamiento por la rampa bajo la acción de su propio peso. La pregunta es: ¿qué forma ha de tener la rampa para que el tiempo sea mínimo? La forma de esta rampa (la forma de la trayectoria) es la braquistócrona: la curva de descenso más rápido. Esta curva no es, en general, una línea recta. Al fin y al cabo, si nuestro móvil se desplaza en línea recta, acelera a ritmo constante durante todo el camino y buena parte del mismo se mueve muy despacio, así que no parece descabellado que una trayectoria distinta, con un tramo inicial más próximo a la vertical que sirva para acelerar mucho al principio del camino, permita alcanzar el destino en menos tiempo.

Solución

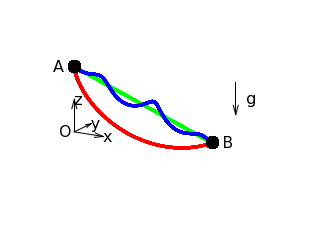
Algunas de las posibles trayectorias entre el punto de origen A y el punto de destino B. Sin pérdida de generalidad, suponemos que el eje x es horizontal y está orientado del punto de origen al punto de destino, z es vertical y apunta hacia arriba (en contra de la gravedad) y el eje y es horizontal y orientado de modo que el triedro xyz está orientado a derechas.

Vamos a resolver este problema con las potentes técnicas del cálculo de variaciones. Definimos, en primer lugar, las siguientes variables:

• g ≡ valor absoluto de la aceleración gravitatoria;
• m ≡ masa del cuerpo;
• s ≡ longitud del arco recorrido por el cuerpo en su trayectoria;
• T ≡ energía cinética del cuerpo en su trayectoria:
  T ≡ (1 ⁄ 2) m v²;
• t ≡ tiempo transcurrido desde el comienzo del movimiento;
• Δt ≡ tiempo total de viaje desde el punto de origen hasta el punto de destino:
  Δt ≡ ∫ds ⁄ v;
• V ≡ energía potencial del cuerpo en su trayectoria:
  V ≡ m g z;
• v ≡ rapidez del cuerpo:
  v ≡ ((dx ⁄ dt)² + (dy ⁄ dt)² + (dz ⁄ dt)²)^1 ⁄ 2 = ds ⁄ dt;
• x ≡ coordenada horizontal longitudinal del cuerpo en su trayectoria;
• x_A ≡ coordenada horizontal longitudinal del punto de partida;
• x_B ≡ coordenada horizontal longitudinaldel punto de destino;
• y ≡ coordenada horizontal lateral del cuerpo en su trayectoria;
• y_A ≡ coordenada horizontal lateral del punto de partida;
• y_B ≡ coordenada horizontal lateral del punto de destino;
• z ≡ coordenada vertical del cuerpo en su trayectoria;
• z_A ≡ coordenada vertical del punto de partida;
• z_B ≡ coordenada vertical del punto de destino.

La ligadura que mantiene al cuerpo pegado a la rampa es holónoma y no trabaja. No hay más interacciones aparte de la gravitatoria, que es conservativa. Por lo tanto, la energía mecánica, igual a la suma de las energías cinética T y potencial V, se conserva. De las expresiones dadas antes, se deduce la siguiente relación entre la rapidez v y la posición vertical z:
v = [2g (z_A − z)]^1 ⁄ 2.
Con esto, la dinámica está esencialmente resuelta y el problema interesante, el del diseño de la braquistócrona, queda facilitado en gran medida.

El tiempo que tarda el cuerpo en recorrer una longitud elemental ds de arco es:
dt = ds ⁄ v.
Si integramos esta expresión entre el punto de partida y el punto destino, obtenemos el tiempo total de viaje Δt:
Δt = ∫ds ⁄ v.
Con la expresión anterior de la rapidez despejada de la ecuación de la energía total, el tiempo total de viaje queda así:
Δt = ∫ds [2g (z_A − z)]^1 ⁄ 2.

Ahora vamos a expresar la anterior integral en función de coordenadas conocidas. Hay varias maneras de hacerlo; nosotros usaremos la coordenada vertical z como variable independiente y de integración y supondremos que podemos obtener una dependencia funcional para las otras dos coordenadas: x(z) y z(z). Esta elección de variables permite que los cálculos sean especialmente sencillos y tiene el interés de no ser la más habitual, pero es singular en algunos puntos que pueden ser de interés (donde la trayectoria es localmente horizontal y en puntos estacionarios de la posición lateral); aun así, la usaremos y a posteriori veremos que podemos prolongar la solución más allá de estos puntos singulares. El elemento de longitud es:
ds = [(dx ⁄ dt)² + (dy ⁄ dt)² + 1]^1 ⁄ 2 dz.
El tiempo total de viaje toma esta forma:
Δt = ∫{[(dx ⁄ dt)² + (dy ⁄ dt)² + 1] ⁄ [2g (z_A − z)]}^1 ⁄ 2 dz.

A partir de aquí, la notación puede volverse un poco pesada. Para simplificar un poco las cosas, introducimos los siguientes símbolos:

• x′ ≡ dx ⁄ dz;
• y′ ≡ dy ⁄ dz;
• I(x′,y′;z) ≡ {[(x′)² + (y′)² + 1] ⁄ [2g (z_A − z)]}^1 ⁄ 2.

Con esta nueva notación, el tiempo de viaje toma una forma muy compacta:
Δt = ∫I(x′,z′;z) dz.

La curva braquistócrona es la trayectoria que minimiza el tiempo de viaje. En el entorno de la braquistócrona, para variaciones infinitesimales arbitrarias (salvo en los puntos de origen y destino, donde no hay variación) δx(z) y δy(z) de las coordenadas horizontales x(z) y y(z), la variación ∂Δt del tiempo de viaje Δt ha de anularse como condición necesaria de mínimo:
∂Δt = 0 ∫(δx′ ∂I ⁄ ∂x′ + δy′ ∂I ⁄ ∂y′) dz;
∂Δt = −∫[δx (d ⁄ dz) ∂I ⁄ ∂x′ + δy (d ⁄ dz) ∂I ⁄ ∂y′] dz.
En la última expresión, hemos hecho uso del hecho de que los puntos de origen y destino son fijos:
δx(z_A) = δy(z_A) = δx(z_B) = δy(z_B) = 0.
Como las variaciones son, por lo demás, arbitrarias, la integral sólo puede ser nula si se cumplen las siguientes condiciones a lo largo de toda la trayectoria:
(d ⁄ dz) ∂I ⁄ ∂x′ = 0;
(d ⁄ dz) ∂I ⁄ ∂y′ = 0.
Éstas son las ecuaciones de Euler-Lagrange del problema de diseño de la braquistócrona.

Una vez obtenidas las ecuaciones diferenciales junto con sus condiciones de contorno (que consisten en obligar a la curva a partir del punto de origen y terminar en el punto de destino), podemos pasar a integrarlas. Vemos que podemos integrar una vez sin esfuerzo:
∂I ⁄ ∂x′ = C_x;
∂I ⁄ ∂y′ = C_y.
C_x y C_y son constantes de integración que podemos relacionar de la siguiente manera con otro juego de constantes C y φ:
C_x = C cos(φ);
C_x = C sin(φ).
Las ecuaciones quedan, una vez desarrolladas, de esta manera:
x′ = C cos(φ) {[z_A − z] [1 + (x′)² + (y′)²]}^1 ⁄ 2;
y′ = C sin(φ) {[z_A − z] [1 + (x′)² + (y′)²]}^1 ⁄ 2.
Ambas ecuaciones tienen la misma forma salvo por factores constantes. Podemos expresar la coordenada lateral y en función de la coordenada longitudinal x:
dy ⁄ dx = y′ ⁄ x′ = tan(φ).
Demostramos con esto que la braquistócrona es una curva plana. Como elegimos los ejes de coordenadas de modo que la coordenada lateral es nula tanto en el origen y_A = 0 como en el destino y_B = 0, deducimos que la coordenada lateral es nula a lo largo de toda la trayectoria: y = 0. Podemos suponer que cos(φ) = 1 y asumir que la constante de integración C puede tener cualquier signo.

Con todo esto, la ecuación diferencial es, finalmente:
x′ = C {[z_A − z] [1 + (x′)²]}^1 ⁄ 2.
Con unas pocas manipulaciones, la ecuación queda claramente en variables separadas:
dx = dz C (z_A − z)^1 ⁄ 2 ⁄ [1 − C² (z_A − z)]^1 ⁄ 2.
Vamos a hacer un cambio de variable: σ ≡ C (z_A − z)^1 ⁄ 2. La ecuación diferencial queda así:
C² dx = −2 σ² dσ ⁄ (1 − σ²)^1 ⁄ 2.
Esta ecuación pide a gritos otro cambio de variable: σ ≡ sin(θ). Con este cambio, nuestra ecuación mejora significativamente su aspecto:
C² dx = −[1 − cos(2θ)] dθ.
Hagamos un último cambio para que la estética mejore un poquito: η ≡ −2θ. La ecuación adopta finalmente este aspecto tan sencillito:
2C² dx = [1 − cos(η)] dη.
Ahora sólo queda hacer una integral que es inmediata. La curva braquistócrona tiene esta forma en función de la variable η:
x = x_A + [η − sin(η)] ⁄ (2C²);
z = z_A − [1 − cos(η)] ⁄ (2C²);
η_A ≤ η ≤ η_B.
Ésta es la curva braquistócrona. Se trata de una cicloide. Esta curva es algo más larga que un camino recto, pero tiene la ventaja de que, al empezar en vertical, permite que el móvil se mueva muy rápido desde muy pronto, lo que compensa la longitud extra.

La braquistócrona es una curva cicloide.

Es fácil comprobar que la condición de contorno de que la curva ha de pasar por el punto origen se cumple con η_A = 0. Las otras dos constantes C y η_B son algo más difíciles de calcular y hay que conseguir sus valores numéricamente o gráficamente. Puede ser útil introducir las variables auxiliares r (la distancia entre el punto de origen y el punto de destino) y m (la pendiente de la línea recta entre el punto de origen y el punto de destino) tales que:
r² ≡ (x_B − x_A)² + (z_B − z_A)²;
m ≡ (z_B − z_A) ⁄ (x_B − x_A).
Tenemos que resolver una ecuación trascendente para obtener η_B en función de m:
[cos(η_B) − 1] ⁄ [η_B − sin(η_B)] = m.
Una vez tenemos el valor de η_B, conocer C (o, mejor, 1 ⁄ (2C²)) es fácil:
1 ⁄ (2C²) = r ⁄ [2 + η_B² − 2η_B sin(η_B) − 2cos(η_B)].

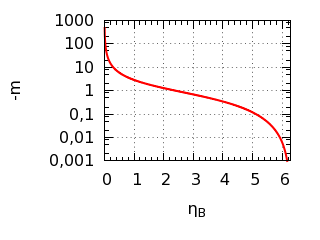
Relación entre la pendiente m de la recta entre el punto de origen y el punto de destino y el parámetro η_B del punto de destino.

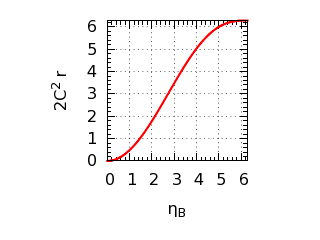
Relación entre el producto de la constante de integración 2C² y la distancia recta r entre los puntos de origen y destino y el parámetro η_B del punto de destino. La singularidad en η_B = 0 es de primer orden y la singularidad en η_B = 2π es de segundo orden.

¡A partir de cierto valor de m, la curva desciende por debajo de z_B y luego vuelve a subir! En principio, tenemos un punto singular si expresamos la posición horizontal x en función de la posición vertical z y nuestro cálculo queda bajo sospecha. Por otra parte, x es una función monótona de η, así que parece que habría sido más riguroso deducir la ecuación diferencial con z en función de x. Habríamos llegado al mismo resultado, cosa que es fácil de comprobar.

Una trayectoria braquistócrona que desciende por debajo de la altura del punto de destino.

Todavía no podemos darnos por satisfechos. Sabemos la forma de la curva, pero no el tiempo de viaje. Afortunadamente, el cálculo no tiene misterio después de haber llegado tan lejos. Lo único que tenemos que hacer es usar lo que sabemos de la solución en la expresión del tiempo de viaje:
t = ∫{[1 + (x′)²] ⁄ [2g (z_A − z)]}^1 ⁄ 2 dz;
t = ∫[2g (z_A − z) (1 − C²)]^−1 ⁄ 2 dz.
La anterior integral va desde el punto de origen hasta un punto cualquiera de la curva para el que queremos saber el tiempo de paso. Hagamos uso de la variable auxiliar σ que tan buenos resultados nos dio antes:
t = ∫−[2 ⁄ (2C² g)] (1 − σ²) dσ = −2asin(σ) ⁄ (2C² g)^1 ⁄ 2.
Si cambiamos a la variable θ y de ahí a la variable η, tenemos la expresión final del tiempo empleado en llegar al punto cuyo parámetro es η:
t = [1 ⁄ (2C²)]^1 ⁄ 2 (η ⁄ √g).
El tiempo de viaje total Δt es:
Δt = [1 ⁄ (2C²)]^1 ⁄ 2 (η_B ⁄ √g).
Este tiempo es inferior al tiempo Δt_s que llevaría cubrir la distancia entre origen y destino en línea recta:
Δt_s = r {2 ⁄ [(z_A − z_B) g]}^1 ⁄ 2.
En efecto, si comparamos los tiempos, nos queda:
Δt ⁄ Δt_s = η_B {[1 − cos(η_B)] ⁄ [2η_B + 4 − 4η_B sin(η_B) − 4cos(η_B)]}^1 ⁄ 2.

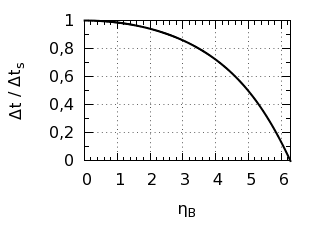
Duración de la trayectoria braquistócrona relativa a la duración de la trayectoria recta. La braquistócrona es más rápida (es decir, el tiempo de viaje Δt es más corto que el tiempo de viaje Δt_s de la trayectoria recta), tanto más cuanto más grande es el parámetro η_B del punto de destino (es decir, cuanto más pequeña es la pendiente de la trayectoria recta).

Categorías: Física, Matemáticas

Artículos publicados el mismo mes

Permalink: http://sgcg.es/articulos/2011/04/19/braquistocrona/

Volver arriba