Abril de 2020
Calendario de artículos de de 2020
| lu | ma | mi | ju | vi | sá | do |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | |||
Píxeles grandes
2020-04-30
Aquí hay otra fotografía píxeles, esta vez de un viejo monitor de un ordenador.
![]()
Píxeles vistos de cerca.
Anteriormente, píxeles:
Categorías: Fotografía
Permalink: https://sgcg.es/articulos/2020/04/30/pixeles-grandes/
Otra fotografía de píxeles
2020-04-29
Aquí hay otra fotografía píxeles de un televisor de pantalla plana.
![]()
Píxeles vistos de cerca.
Anteriormente, píxeles:
Categorías: Fotografía
Permalink: https://sgcg.es/articulos/2020/04/29/otra-fotografia-de-pixeles/
El modelo epidemiológico SIR (12)
2020-04-28
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:
- cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia;
- el comportamiento de la proporción de infectados en esta fase inicial;
- cómo relacionar las variables sin necesidad de integrar en el tiempo;
- cómo calcular el máximo número de infectados simultáneos;
- cómo calcular el resultado final de la epidemia;
- cómo se comporta la epidemia en el entorno del máximo de infectados simultáneos;
- cómo varían los infectados cerca del final de la epidemia;
- cómo se relacionan la fase de crecimiento exponencial inicial de la epidemia y la fase de decrecimiento exponencial final de la epidemia;
- qué condición es necesaria para la inmunidad de grupo;
- cómo queda modificado el modelo si en vez de trabajar con proporciones sobre la población total, trabajamos con números absolutos de individuos.
Hoy veremos cómo plantear el modelo cuando hay nacimientos y defunciones, pero la población total se mantiene estable.
El modelo sigue a lo largo del tiempo t la evolución de la población susceptible S(t), la población infectada I(t) y la población recuperada (inmune) R(t). Este modelo va a cumplir los siguientes criterios, que son muy similares a los del modelo SIR sin nacimientos ni defunciones:
- la población es tan grande que es legítimo asumir que varía de forma continua en número de individuos y a lo largo del tiempo;
- todo individuo nace en el estado susceptible;
- los nacimientos por unidad de tiempo son proporcionales a la población;
- las defunciones por unidad de tiempo son proporcionales a la población;
- los nacimientos son iguales a las defunciones;
- los susceptibles pasan a infectarse a un ritmo que es proporcional a la población susceptible y proporcional a la población infectada (hay más infecciones conforme más infectados entran en contacto con más susceptibles);
- los infectados pasan a recuperarse a un ritmo que es proporcional a la población infectada (hay más recuperaciones conforme hay más infectados por recuperar);
- los recuperados adquieren inmunidad permanente;
- la dinámica no depende del tiempo.
Con estas condiciones, podemos establecer el siguiente sistema (casi idéntico al visto hasta el momento) de ecuaciones diferenciales ordinarias:
dS ⁄ dt = μ N − β S I ⁄ N − μ S;
dI ⁄ dt = β S I ⁄ N − γ I − μ I;
dR ⁄ dt = γ I − μ R.
Aparecen varios símbolos cuyo significado es el siguiente:
- El símbolo N denota la población total, S + I + R, que se mantiene constante. Como anteriormente, como la población es constante, es muy cómodo tomar N = 1 y trabajar con proporciones de la población total.
- El símbolo μ denota tanto la natalidad como la mortalidad, que son iguales.
- El símbolo β denota la tasa de infección. En anteriores artículos era el ritmo reproductivo básico dividido entre el tiempo infeccioso promedio, pero ahora los nacimientos y las defunciones complican un poco la interpretación.
- El símbolo γ denota la tasa de recuperación de los infectados. En anteriores artículos era el inverso del tiempo infeccioso promedio, pero ahora las defunciones complican un poco la interpretación.
Incluso esta complicación tan pequeña del modelo elemental hace que sea posible modelar nuevos fenómenos muy interesantes cuando los sujetos se reproducen con tiempos característicos no muy alejados de los de la propia enfermedad.
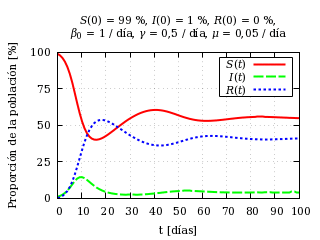
Dinámica de una epidemia en una hipotética población de animales
(quizá roedores).
Categorías: Matemáticas, Salud
Permalink: https://sgcg.es/articulos/2020/04/28/el-modelo-epidemiologico-sir-12/
Anecdato
2020-04-27
«Anecdato» es una anécdota camuflada como un dato: evidencia anecdótica. Que una afirmación esté respaldada por evidencia anecdótica no invalida dicha afirmación; es la ausencia de evidencia rigurosa lo que hace que una afirmación quede en entredicho. Una persona malintencionada puede presentar una pila abrumadora de anecdatos para tratar de engañar a su interlocutor.
Categorías: Lingüística
La diferencia entre «inmoral» y «amoral»
2020-04-26
Los adjetivos «inmoral» y «amoral», aunque se parecen superficialmente, tienen diferencias muy importantes:
- Inmoral es lo que se opone a la moral.
- Amoral es una persona que carece de sentido moral o una obra sin fin moral.
Los actos de una persona amoral pueden ser conformes a la moral de cualquier observador externo y también pueden ser opuestos a la moral de dicho observador externo, pero tal conformancia u oposición es, en principio, accidental para el sujeto amoral, ya que el criterio moral le es ajeno.
Criticar un acto por amoral es probablemente improductivo a menos que se considere una inmoralidad no dar fin moral a un acto. ¡Entretenido!
Categorías: Lingüística
Permalink: https://sgcg.es/articulos/2020/04/26/la-diferencia-entre-inmoral-y-amoral/
El modelo epidemiológico SIR (11)
2020-04-21
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:
- cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia;
- el comportamiento de la proporción de infectados en esta fase inicial;
- cómo relacionar las variables sin necesidad de integrar en el tiempo;
- cómo calcular el máximo número de infectados simultáneos;
- cómo calcular el resultado final de la epidemia;
- cómo se comporta la epidemia en el entorno del máximo de infectados simultáneos;
- cómo varían los infectados cerca del final de la epidemia;
- cómo se relacionan la fase de crecimiento exponencial inicial de la epidemia y la fase de decrecimiento exponencial final de la epidemia;
- qué condición es necesaria para la inmunidad de grupo.
Hoy veremos cómo queda modificado el modelo si en vez de trabajar con proporciones sobre la población total, trabajamos con números absolutos de individuos.
Recordemos que el modelo sigue a lo largo del tiempo t la evolución de la proporción de susceptibles S(t), la proporción de infectados I(t) y la proporción de recuperados (inmunes y fallecidos) R(t) mediante el siguiente sistema de ecuaciones diferenciales ordinarias:
dS ⁄ dt = −(R0 ⁄ tI) S I;
dI ⁄ dt = (R0 ⁄ tI) S I − (1 ⁄ tI) I;
dR ⁄ dt = (1 ⁄ tI) I.
El parámetro R0 es el ritmo reproductivo básico: el número medio de contagios por infectado cuando toda la población es susceptible. El parámetro tI es el tiempo medio que permanece un paciente infectado.
S, I y R en las anteriores ecuaciones son proporciones sobre la población total, que es de N individuos. Si en vez de hablar de proporciones, usamos las cantidades absolutas de invidivuos S' ≝ N S, I' ≝ N I y R' ≝ N R, es inmediato concluir que las ecuaciones quedan de la siguiente manera:
dS' ⁄ dt = −[R0 ⁄ (N tI)] S' I';
dI' ⁄ dt = [R0 ⁄ (N tI)] S' I' − (1 ⁄ tI) I';
dR' ⁄ dt = (1 ⁄ tI) I'.
Esto implica que los cálculos de los anteriores artículos son aplicables de inmediato de dos formas muy cómodas:
- bien trabajando en proporciones sobre la población total y escalando con N los resultados para obtener los números de individuos;
- bien trabajando directamente en número de individuos (tomando que S, I y R se refieren a números de individuos en vez de a proporciones sobre la población total) y escribiendo R0 ⁄ N allí donde en las ecuaciones referidas a proporciones de población aparece R0.
Categorías: Matemáticas, Salud
Permalink: https://sgcg.es/articulos/2020/04/21/el-modelo-epidemiologico-sir-11/
El modelo epidemiológico SIR (10)
2020-04-18
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:
- cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia;
- el comportamiento de la proporción de infectados en esta fase inicial;
- cómo relacionar las variables sin necesidad de integrar en el tiempo;
- cómo calcular el máximo número de infectados simultáneos;
- cómo calcular el resultado final de la epidemia;
- cómo se comporta la epidemia en el entorno del máximo de infectados simultáneos;
- cómo varían los infectados cerca del final de la epidemia;
- cómo se relacionan la fase de crecimiento exponencial inicial de la epidemia y la fase de decrecimiento exponencial final de la epidemia.
Hoy veremos qué condición es necesaria para la inmunidad de grupo en este modelo.
Recordemos que el modelo sigue a lo largo del tiempo t la evolución de la proporción de susceptibles S(t), la proporción de infectados I(t) y la proporción de recuperados (inmunes y fallecidos) R(t) mediante el siguiente sistema de ecuaciones diferenciales ordinarias:
dS ⁄ dt = −(R0 ⁄ tI) S I;
dI ⁄ dt = (R0 ⁄ tI) S I − (1 ⁄ tI) I;
dR ⁄ dt = (1 ⁄ tI) I.
El parámetro R0 es el ritmo reproductivo básico: el número medio de contagios por infectado cuando toda la población es susceptible. El parámetro tI es el tiempo medio que permanece un paciente infectado.
La inmunidad de grupo se alcanza cuando la proporción de inmunes (R en este modelo) que la proporción de susceptibles es insuficiente para que, partiendo de una cantidad no nula de infectados, el número de infectados crezca. Es decir, ha de cumplirse lo siguiente:
dI ⁄ dt < 0.
De acuerdo con el modelo, la anterior condición implica esto:
(R0 ⁄ tI) S I − (1 ⁄ tI) I < 0.
Ahora bien, como el número de infectados de partida y la vida media de la infección son superiores a 0, la condición puede simplificarse un poco:
R0 S − 1 < 0.
Ahora bien, la población es constante en este modelo, así que se cumple que
S + I + R = 1,
con lo que tenemos la siguiente condición:
R0 (1−I−R) − 1 < 0.
Es inmediato dejar una condición explícita para los inmunes:
R > 1 − I − 1 ⁄ R0.
A partir del momento en el que se cumple esta condición, la infección empieza a disiparse. Una condición más exigente, que es válida independientemente de la proporción de infectados, es la siguiente:
R > 1 − 1 ⁄ R0.
Esta condición es la condición de inmunidad de grupo que implica que la epidemia no puede darse. El número acumulado de infecciones puede crecer a partir de un instante inicial, pero no de forma descontrolada, sino a un ritmo decreciente desde el primer momento.
La siguiente figura muestra, en función del ritmo reproductivo básico, el valor límite de la proporción de inmunes que hace falta de acuerdo con este modelo para alcanzar la inmunidad de grupo:
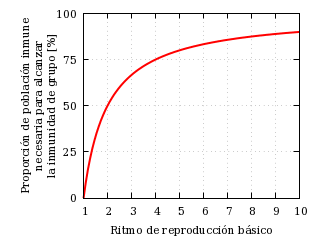
Inmunizados necesarios para alcanzar la inmunidad de grupo frente
al ritmo reproductivo básico.
Categorías: Matemáticas, Salud
Permalink: https://sgcg.es/articulos/2020/04/18/el-modelo-epidemiologico-sir-10/
El modelo epidemiológico SIR (9)
2020-04-12
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:
- cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia;
- el comportamiento de la proporción de infectados en esta fase inicial;
- cómo relacionar las variables sin necesidad de integrar en el tiempo;
- cómo calcular el máximo número de infectados simultáneos;
- cómo calcular el resultado final de la epidemia;
- cómo se comporta la epidemia en el entorno del máximo de infectados simultáneos;
- cómo varían los infectados cerca del final de la epidemia.
Hoy veremos cómo se relacionan la fase de crecimiento exponencial inicial de la epidemia y la fase de decrecimiento exponencial final de la epidemia.
Recordemos que el modelo sigue a lo largo del tiempo t la evolución de la proporción de susceptibles S(t), la proporción de infectados I(t) y la proporción de recuperados (inmunes y fallecidos) R(t) mediante el siguiente sistema de ecuaciones diferenciales ordinarias:
dS ⁄ dt = −(R0 ⁄ tI) S I;
dI ⁄ dt = (R0 ⁄ tI) S I − (1 ⁄ tI) I;
dR ⁄ dt = (1 ⁄ tI) I.
El parámetro R0 es el ritmo reproductivo básico: el número medio de contagios por infectado cuando toda la población es susceptible. El parámetro tI es el tiempo medio que permanece un paciente infectado.
La epidemia crece de forma exponencial inicialmente cuando casi toda la población es susceptible: S(0) ≅ 1, I(0) ≪ 1, R(0) ≪ 0. Como vimos anteriormente, al principio de la epidemia, el número de infectados tiene un crecimiento exponencial como sigue:
I(t) ∝ e[(R0−1) ⁄ tI] t, t → 0.
También vimos que, al final de la epidemia, el número de infectados tiene un decrecimiento exponencial como sigue:
I(t) ∝ e−{[1−R0 S(∞)] ⁄ tI} t, t → ∞.
En la relación anterior aparece el valor de la proporción de susceptibles cuando la epidemia se ha disipado, S(∞). Vimos que este valor sale de las siguientes ecuaciones que se cumplen con la condición inicial simplificada S(0) = 1, R(0) = 0:
e−R0 R(∞) + R(∞) = 1;
S(∞) = 1 − R(∞).
Con toda esta información, podemos comparar el comportamiento de la epidemia en la fase inicial con el comportamiento de la epidemia en la fase final. En escala logarítmica y tomando como unidad de tiempo tI, los infectados crecen inicialmente con el factor de crecimiento R0−1 y decrecen finalmente con el factor de decrecimiento 1−R0 S(∞). Las siguientes curvas ilustran cómo varían ambos factores en función de R0:
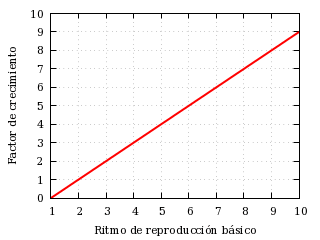
Factor de crecimiento.
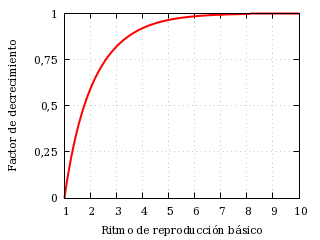
Factor de decrecimiento.
El comportamiento no es simétrico, sino que la fase de decrecimiento final es menos empinada que la fase de decrecimiento final. Esto puede verse fácilmente si se traza la razón entre el factor de decrecimiento y el factor de crecimiento en función de R0:
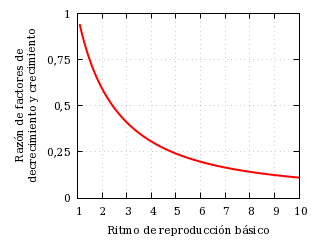
Relación de factores de decrecimiento final y crecimiento inicial.
La relación cae hasta anularse en el límite R0 → ∞. Esto no se debe a que la fase de decrecimiento se suaviza, sino a que la fase de crecimiento se hace abrupta muy rápidamente. Como se ve, la curva de decrecimiento final se hace más y más empinada conforme crece R0; esto se debe a que se agotan los susceptibles que pueden renovar la población de infectados.
Categorías: Matemáticas, Salud
Permalink: https://sgcg.es/articulos/2020/04/12/el-modelo-epidemiologico-sir-9/
El modelo epidemiológico SIR (8)
2020-04-11
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:
- cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia;
- el comportamiento de la proporción de infectados en esta fase inicial;
- cómo relacionar las variables sin necesidad de integrar en el tiempo;
- cómo calcular el máximo número de infectados simultáneos;
- cómo calcular el resultado final de la epidemia;
- cómo se comporta la epidemia en el entorno del máximo de infectados simultáneos.
Hoy estudiaremos cómo varían los infectados cerca del final de la epidemia.
Recordemos que el modelo sigue a lo largo del tiempo t la evolución de la proporción de susceptibles S(t), la proporción de infectados I(t) y la proporción de recuperados (inmunes y fallecidos) R(t) mediante el siguiente sistema de ecuaciones diferenciales ordinarias:
dS ⁄ dt = −(R0 ⁄ tI) S I;
dI ⁄ dt = (R0 ⁄ tI) S I − (1 ⁄ tI) I;
dR ⁄ dt = (1 ⁄ tI) I.
El parámetro R0 es el ritmo reproductivo básico: el número medio de contagios por infectado cuando toda la población es susceptible. El parámetro tI es el tiempo medio que permanece un paciente infectado.
Tras un tiempo largo, la epidemia acaba extinguiéndose de acuerdo con el modelo. Como vimos, los infectados tienden a anularse, mientra que los susceptibles S(∞) y los recuperados R(∞) satisfacen las siguientes ecuaciones:
S(0) e−R0 [R(∞)−R(0)] + R(∞) = 1;
S(∞) = 1 − R(∞).
En tiempos largos, el valor de S(t) será muy similar a S(∞), así que podemos aproximar la dinámica de los infectados de la siguiente manera:
dI ⁄ dt ≃ (R0 ⁄ tI) S(∞) I − (1 ⁄ tI) I, t→∞.
De esto se deduce que el número de infectados varía aproximadamente de la siguiente manera a partir de un tiempo grande td:
I(t) ≅ I(td) e−{[1−R0 S(∞)] ⁄ tI} (t−td), t→∞.
Igual que los infectados crecen exponencialmente al comienzo de la epidemia, decrecen exponencialmente al final de la epidemia.
Categorías: Matemáticas, Salud
Permalink: https://sgcg.es/articulos/2020/04/11/el-modelo-epidemiologico-sir-8/
El modelo epidemiológico SIR (7)
2020-04-06
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:
- cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia;
- el comportamiento de la proporción de infectados en esta fase inicial;
- cómo relacionar las variables sin necesidad de integrar en el tiempo;
- cómo calcular el máximo número de infectados simultáneos;
- cómo calcular el resultado final de la epidemia.
Hoy estudiaremos el comportamiento de la epidemia en el entorno del pico de contagios.
Recordemos que el modelo sigue a lo largo del tiempo t la evolución de la proporción de susceptibles S(t), la proporción de infectados I(t) y la proporción de recuperados (inmunes y fallecidos) R(t) mediante el siguiente sistema de ecuaciones diferenciales ordinarias:
dS ⁄ dt = −(R0 ⁄ tI) S I;
dI ⁄ dt = (R0 ⁄ tI) S I − (1 ⁄ tI) I;
dR ⁄ dt = (1 ⁄ tI) I.
El parámetro R0 es el ritmo reproductivo básico: el número medio de contagios por infectado cuando toda la población es susceptible. El parámetro tI es el tiempo medio que permanece un paciente infectado.
De acuerdo con el modelo elemental SIR, el número de infectados simultáneos crece inicialmente hasta alcanzar un máximo y, después, cae hasta anularse. Este máximo se produce cuando transcurre un tiempo tm desde el instante inicial t = 0; de acuerdo con lo visto hace unos días, las variables quedan así en el máximo:
S(tm) = 1 ⁄ R0;
I(tm) = I(0) + S(0) − 1 ⁄ R0 − (1 ⁄ R0) log[R0 S(0)];
R(tm) = (1 ⁄ R0) log[R0 S(0)] + R(0).
Los primeros términos del desarrollo en serie de Taylor nos permiten examinar el comportamiento del sistema en el entorno del máximo de infecciones:
S(t) ≅ S(tm) + (dS ⁄ dt)(tm) (t−tm) = S(tm) [1 − (R0 ⁄ tI) I(tm) (t−tm)].
I(t) ≅ I(tm) + (1 ⁄ 2) (d2I ⁄ dt2)(tm) (t−tm)2 = I(tm) {1 − (1 ⁄ 2) (R0 ⁄ tI)2 S(tm) [I(tm)]2 (t−tm)2};
R(t) ≅ R(tm) + (dR ⁄ dt)(tm) (t−tm) = R(tm) + (1 ⁄ tI) I(tm) (t−tm).
Tanto los susceptibles como los recuperados quedan aproximados mediante una recta; los infectados quedan aproximados mediante una parábola. Si tomamos más términos del desarrollo en serie, podemos deducir más información:
- la curva de susceptibles en función del tiempo no tiene un punto de inflexión en el instante de máximos contagios: cae a un ritmo cada vez más lento;
- la curva de infectados en función del tiempo en general no es simétrica alrededor del máximo (los términos impares de orden superior a la unidad del desarrollo en serie son no nulos);
- la curva de recuperados en función del tiempo tiene un punto de inflexión en el instante de máximo de infectados y pasa allí de crecer cada vez más rápido a crecer cada vez más despacio.
Categorías: Matemáticas, Salud
Permalink: https://sgcg.es/articulos/2020/04/06/el-modelo-epidemiologico-sir-7/
El ritmo reproductivo básico no es en general lo que crecen los enfermos de un día a otro
2020-04-04
Estamos en medio de una preocupante epidemia y la situación se hace llevadera hablando de epidemiología. El incauto lector que haya pasado por esta página el último mes puede ver un ejemplo de ello. ¡Es potencialmente beneficioso! Ahora bien, hay que evitar esparcir desinformación y los errores. Un error de concepto que estoy viendo con cierta frecuencia es la confusión entre el ritmo reproductivo básico de una epidemia (R0) y lo que crece el número de casos de un día para otro. El ritmo reproductivo básico, la famosa R0, es el número esperado de contagios que provoca directamente un infectado cuando el resto de la población son susceptibles al contagio. Por lo tanto, por norma general, la razón entre el número de casos un día y el número de casos el día anterior no ha de coincidir con el ritmo reproductivo básico. Serían esencialmente lo mismo solamente en infecciones que duran un día y se extienden lentamente. Es fácil estimar la relación entre R0 y el ritmo diario de crecimiento con un modelo compartimental elemental. La diferencia se hace evidente si imaginamos, por decir algo, una nueva enfermedad en la cada caso contagia a otras 5 personas tras 15 días; en esta situación, a pesar de que R0 es 5, los contagios se multiplican por más o menos 1,3 cada día al comienzo de la epidemia, que es algo muy alejado de quintuplicar los casos (y, de igual manera, no puede decirse que R0 sea 1,3).
Categorías: Salud
