El modelo epidemiológico SIR (1)
2020-03-16
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Divide a la población en tres compartimentos: susceptibles de padecer una enfermedad, pacientes infectados y pacientes recuperados, inmunes y fallecidos. La evolución temporal de la población en cada uno de estos compartimentos queda modelada mediante una ecuación diferencial ordinaria que es fácil de resolver con un ordenador. Veamos con más detalle las características del modelo:
- El modelo sirve para calcular la evolución de la población en cada compartimento en función del tiempo t transcurrido desde un instante inicial.
- La proporción de población susceptible con respecto a la población total es S(t).
- La proporción de población infectada con respecto a la población total es I(t).
- La proporción de población recuperada (que también incluye a los previamente inmunes y a los fallecidos) con respecto a la población total es R(t).
- La población total no varía: S(t) + I(t) + R(t) = 1.
- Las personas susceptibles pueden pasar a ser infectadas o permanecer susceptibles.
- Las personas infectadas acaban pasando a ser recuperadas.
- Las personas recuperadas permanecen recuperadas: bien adquieren inmunidad, bien fallecen.
- La recuperación de la enfermedad es un proceso de Poisson con vida media tI. Las recuperaciones por unidad de tiempo serán, por lo tanto, proporcionales al número de infectados.
- La transmisión de la enfermedad también es un proceso de Poisson con un número medio de nuevos casos R0 por paciente infectado cuando toda la población es susceptible. Este número R0 es la famosa tasa de reproducción básica. Si la población susceptible decrece, decrecen igualmente las oportunidades de transmisión, con lo que las infecciones por unidad de tiempo serán proporcionales al número de susceptibles y al número de infectados.
De estas características se deduce la siguiente dinámica:
dS ⁄ dt = −(R0 ⁄ tI) S I;
dI ⁄ dt = (R0 ⁄ tI) S I − (1 ⁄ tI) I;
dR ⁄ dt = (1 ⁄ tI) I.
Integrar estas ecuaciones a partir de una condición inicial {S(0), I(0), R(0)} permite estimar cómo puede evolucionar una epidemia.
Aunque este modelo es muy sencillo, muestra una dinámica interesante y realista con infecciones que crecen hasta alcanzar un máximo y acaban decayendo. Las hipótesis en las que se basa el modelo son cuestionables en algunas ocasiones, pero otras veces son bastante razonables.
Veremos en próximas entregas más detalles sobre este modelo. Por ahora, para causar un poco de incomodidad, he aquí un escenario a 100 días de una enfermedad muy contagiosa para la que la población no tiene inmunidad:
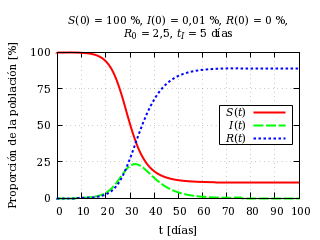
Evolución temporal de una epidemia.
Categorías: Matemáticas, Salud
Permalink: https://sgcg.es/articulos/2020/03/16/el-modelo-epidemiologico-sir-1/
