El modelo epidemiológico SIR (9)
2020-04-12
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:
- cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia;
- el comportamiento de la proporción de infectados en esta fase inicial;
- cómo relacionar las variables sin necesidad de integrar en el tiempo;
- cómo calcular el máximo número de infectados simultáneos;
- cómo calcular el resultado final de la epidemia;
- cómo se comporta la epidemia en el entorno del máximo de infectados simultáneos;
- cómo varían los infectados cerca del final de la epidemia.
Hoy veremos cómo se relacionan la fase de crecimiento exponencial inicial de la epidemia y la fase de decrecimiento exponencial final de la epidemia.
Recordemos que el modelo sigue a lo largo del tiempo t la evolución de la proporción de susceptibles S(t), la proporción de infectados I(t) y la proporción de recuperados (inmunes y fallecidos) R(t) mediante el siguiente sistema de ecuaciones diferenciales ordinarias:
dS ⁄ dt = −(R0 ⁄ tI) S I;
dI ⁄ dt = (R0 ⁄ tI) S I − (1 ⁄ tI) I;
dR ⁄ dt = (1 ⁄ tI) I.
El parámetro R0 es el ritmo reproductivo básico: el número medio de contagios por infectado cuando toda la población es susceptible. El parámetro tI es el tiempo medio que permanece un paciente infectado.
La epidemia crece de forma exponencial inicialmente cuando casi toda la población es susceptible: S(0) ≅ 1, I(0) ≪ 1, R(0) ≪ 0. Como vimos anteriormente, al principio de la epidemia, el número de infectados tiene un crecimiento exponencial como sigue:
I(t) ∝ e[(R0−1) ⁄ tI] t, t → 0.
También vimos que, al final de la epidemia, el número de infectados tiene un decrecimiento exponencial como sigue:
I(t) ∝ e−{[1−R0 S(∞)] ⁄ tI} t, t → ∞.
En la relación anterior aparece el valor de la proporción de susceptibles cuando la epidemia se ha disipado, S(∞). Vimos que este valor sale de las siguientes ecuaciones que se cumplen con la condición inicial simplificada S(0) = 1, R(0) = 0:
e−R0 R(∞) + R(∞) = 1;
S(∞) = 1 − R(∞).
Con toda esta información, podemos comparar el comportamiento de la epidemia en la fase inicial con el comportamiento de la epidemia en la fase final. En escala logarítmica y tomando como unidad de tiempo tI, los infectados crecen inicialmente con el factor de crecimiento R0−1 y decrecen finalmente con el factor de decrecimiento 1−R0 S(∞). Las siguientes curvas ilustran cómo varían ambos factores en función de R0:
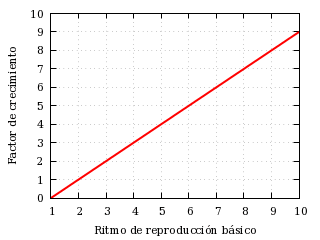
Factor de crecimiento.
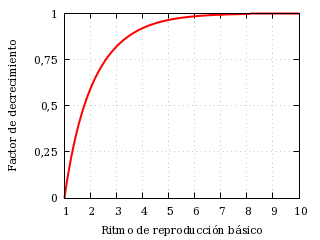
Factor de decrecimiento.
El comportamiento no es simétrico, sino que la fase de decrecimiento final es menos empinada que la fase de decrecimiento final. Esto puede verse fácilmente si se traza la razón entre el factor de decrecimiento y el factor de crecimiento en función de R0:
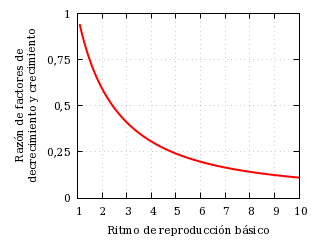
Relación de factores de decrecimiento final y crecimiento inicial.
La relación cae hasta anularse en el límite R0 → ∞. Esto no se debe a que la fase de decrecimiento se suaviza, sino a que la fase de crecimiento se hace abrupta muy rápidamente. Como se ve, la curva de decrecimiento final se hace más y más empinada conforme crece R0; esto se debe a que se agotan los susceptibles que pueden renovar la población de infectados.
Categorías: Matemáticas, Salud
Permalink: http://sgcg.es/articulos/2020/04/12/el-modelo-epidemiologico-sir-9/
