El modelo epidemiológico SIR (12)
2020-04-28
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:
- cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia;
- el comportamiento de la proporción de infectados en esta fase inicial;
- cómo relacionar las variables sin necesidad de integrar en el tiempo;
- cómo calcular el máximo número de infectados simultáneos;
- cómo calcular el resultado final de la epidemia;
- cómo se comporta la epidemia en el entorno del máximo de infectados simultáneos;
- cómo varían los infectados cerca del final de la epidemia;
- cómo se relacionan la fase de crecimiento exponencial inicial de la epidemia y la fase de decrecimiento exponencial final de la epidemia;
- qué condición es necesaria para la inmunidad de grupo;
- cómo queda modificado el modelo si en vez de trabajar con proporciones sobre la población total, trabajamos con números absolutos de individuos.
Hoy veremos cómo plantear el modelo cuando hay nacimientos y defunciones, pero la población total se mantiene estable.
El modelo sigue a lo largo del tiempo t la evolución de la población susceptible S(t), la población infectada I(t) y la población recuperada (inmune) R(t). Este modelo va a cumplir los siguientes criterios, que son muy similares a los del modelo SIR sin nacimientos ni defunciones:
- la población es tan grande que es legítimo asumir que varía de forma continua en número de individuos y a lo largo del tiempo;
- todo individuo nace en el estado susceptible;
- los nacimientos por unidad de tiempo son proporcionales a la población;
- las defunciones por unidad de tiempo son proporcionales a la población;
- los nacimientos son iguales a las defunciones;
- los susceptibles pasan a infectarse a un ritmo que es proporcional a la población susceptible y proporcional a la población infectada (hay más infecciones conforme más infectados entran en contacto con más susceptibles);
- los infectados pasan a recuperarse a un ritmo que es proporcional a la población infectada (hay más recuperaciones conforme hay más infectados por recuperar);
- los recuperados adquieren inmunidad permanente;
- la dinámica no depende del tiempo.
Con estas condiciones, podemos establecer el siguiente sistema (casi idéntico al visto hasta el momento) de ecuaciones diferenciales ordinarias:
dS ⁄ dt = μ N − β S I ⁄ N − μ S;
dI ⁄ dt = β S I ⁄ N − γ I − μ I;
dR ⁄ dt = γ I − μ R.
Aparecen varios símbolos cuyo significado es el siguiente:
- El símbolo N denota la población total, S + I + R, que se mantiene constante. Como anteriormente, como la población es constante, es muy cómodo tomar N = 1 y trabajar con proporciones de la población total.
- El símbolo μ denota tanto la natalidad como la mortalidad, que son iguales.
- El símbolo β denota la tasa de infección. En anteriores artículos era el ritmo reproductivo básico dividido entre el tiempo infeccioso promedio, pero ahora los nacimientos y las defunciones complican un poco la interpretación.
- El símbolo γ denota la tasa de recuperación de los infectados. En anteriores artículos era el inverso del tiempo infeccioso promedio, pero ahora las defunciones complican un poco la interpretación.
Incluso esta complicación tan pequeña del modelo elemental hace que sea posible modelar nuevos fenómenos muy interesantes cuando los sujetos se reproducen con tiempos característicos no muy alejados de los de la propia enfermedad.
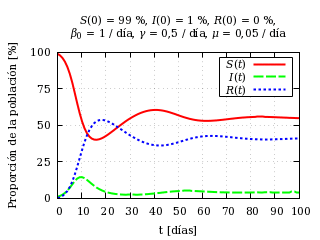
Dinámica de una epidemia en una hipotética población de animales
(quizá roedores).
Categorías: Matemáticas, Salud
Permalink: https://sgcg.es/articulos/2020/04/28/el-modelo-epidemiologico-sir-12/
