Septiembre de 2013

lu	ma	mi	ju	vi	sá	do
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30

Jugando con autómatas celulares (18)

2013-09-29

Hace varios artículos, planteamos un interesante proyecto: una pequeña biblioteca para construir autómatas celulares. Los autómatas celulares son unas estructuras matemáticas muy curiosas: retículos de celdas que van cambiando de un estado a otro y que pueden, a partir de reglas sencillas, exhibir complejísimos comportamientos emergentes. Como práctica, nuestra biblioteca estará hecha en Scheme R5RS y en Python 2. El enfoque es funcional porque el problema se presta mucho a ello. No nos preocuparemos tanto por hacer un código especialmente rápido como por hacerlo claro y conciso.

Dicho lo anterior, nuestra biblioteca está bien para explorar, pero estaría mejor si pudiéramos hacer que fuera un poquito más deprisa. Hicimos algunas mejoras en un artículo anterior; hoy veremos algunas más. No conseguiremos algo tan rápido como un programa especializado y optimizado a mano en C, pero conseguiremos una ganancia importante con poco trabajo.

Acceso aleatorio a elementos de la lista de celdas en Scheme

La función matrix-ref de nuestra biblioteca sirve para acceder a elementos de la lista de celdas en posiciones aleatorias. Como esta lista es simplemente enlazada en la versión de la biblioteca hecha en Scheme, el acceso es lineal. Cualquier función que recorra todos los elementos de la lista de celdas mediante matrix-ref incurrirá en un coste no lineal, sino cuadrático. Esto puede ser algo lento, pero la solución es muy fácil: no tenemos más que hacer que matrix-ref funcione también con vectores y hacer la conversión necesaria mediante list->vector (cuyo coste es lineal con el tamaño de la lista de celdas) antes de empezar a trabajar con matrix-ref. La versión modificada de nuestra función es así:
(define (matrix-ref matrix sizes indices) (let ((ref (if (vector? matrix) vector-ref list-ref))) (ref matrix (multidimensional->flat sizes indices))))

La función translate-and-display-cartesian-2d que usamos para mostrar por pantalla las mallas cartesianas bidimensionales de autómatas como el del juego de la vida de Conway es una de las funciones ofensoras que hacen uso de matrix-ref, aunque no directamente, sino a través de una función auxiliar llamada cartesian-rows que extrae una lista de filas del retículo de celdas del autómata. Hacemos que la función funcione con vectores sin más que añadir una línea y modificar otra. El resultado es así:
(define (cartesian-rows cells sizes) (let ((rows (car sizes)) (columns (cadr sizes)) (matrix (list->vector cells))) (map (lambda (row) (map (lambda (column) (matrix-ref matrix sizes (list row column))) (range 0 columns 1))) (range 0 rows 1))))
La ganancia al actuar así es enorme.

Memoización de las funciones de aritmética de índices

Las funciones de aritmética de índices son muy generales y permiten trabajar con dimensiones arbitrariamente grandes gracias al uso generoso de map, fold y unfold con listas de dimensiones, pero a cambio son algo lentas, especialmente en Python (si usamos CPython, que es la implementación de referencia), ya que el intérprete es muy lento a la hora de hacer llamadas a funciones. Podemos hacer las cosas más rápidas si experimentamos con @memoise delante de las funciones flat_to_multidimensional, multidimensional_to_flat y cyclic_addition. Antes de rehacer cyclic_cartesian_neighbourhoods como en el anterior artículo de la serie, podríamos haber decorado las funciones problemáticas con @memoised para obtener mejoras de rendimiento un poquito menores, pero muy considerables.

Aceleración de la función de extracción de filas

La función de extracción de filas todavía puede correr un poquito más si usamos técnicas de memoización para construir los índices con una pequeña reescritura como la que aplicamos en cyclic-cartesian-neighbourhoods. La ganancia puede ser ya muy pequeña. Si asumimos que existe una función llamada cartesian-row-indices que acepta una lista sizes de tamaños y un número de fila row y devuelve una lista con los índices planos correspondientes a esa fila, la función cartesian-rows puede simplificarse un poquito:
(define (cartesian-rows cells sizes) (let ((rows (car sizes)) (columns (cadr sizes)) (matrix (list->vector cells))) (map (lambda (row) (map (lambda (index) (vector-ref matrix index)) (cartesian-row-indices sizes row))) (range 0 rows 1))))
Eso era Scheme. La versión de Python es así:
def cartesian_rows(cells, sizes): rows, columns = sizes return map(lambda row: map(lambda index: cells[index], cartesian_row_indices(sizes, row)), range(0, rows, 1))
Lo que hacemos es dejar de operar con matrix-ref y acceder a los elementos de la lista plana de celdas directamente. La función cartesian-row-indices con memoización necesaria es así en Scheme:
(define-memoised (cartesian-row-indices sizes row) (let ((columns (cadr sizes))) (map (lambda (column) (multidimensional->flat sizes (list row column))) (range 0 columns 1))))
Es así en Python:
@memoise def cartesian_row_indices(sizes, row): columns = sizes[1] indices = map(lambda column: multidimensional_to_flat(sizes, (row, column)), range(0, columns, 1)) return indices

Otros artículos de la serie

Categorías: Informática

Permalink: https://sgcg.es/articulos/2013/09/29/jugando-con-automatas-celulares-18/

30 aniversario de GNU

2013-09-27

Hoy se cumplen 30 años del anuncio inicial del proyecto GNU efectuado por Richard Stallman, un hombre que ha dedicado su vida a luchar por la libertad en un terreno tan pintoresco como el del software. Esto sucedió tal día como hoy, un 27 de septiembre de 1983, en los grupos de noticias net.unix-wizards y net.usoft; con ello, más o menos se le dio el pistoletazo de salida oficial al movimiento del software libre. El proyecto GNU está en plena celebración.

Un poco de historia

Hasta unos años antes del anuncio del proyecto GNU, el software solía ser libre de facto aunque no de jure, pero rápidamente se extendió el modelo del software propietario o privativo, software que emplea medidas tanto técnicas (como ocultar el funcionamiento interno del programa) como legales (copyright y contratos) para evitar la competencia en un mercado libre y mantener a los clientes cautivos. Esto, que era algo inaudito hasta entonces y atentaba contra la cultura hacker, propició que algunas personas como Richard Stallman reaccionaran e hicieran un esfuerzo para restablecer de forma explícita las libertades que solían acompañar al software anteriormente. Estos esfuerzos se plasmaron en varios proyectos; entre ellos, se encuentra el proyecto GNU que cumple 30 años desde su concepción.

En qué consiste exactamente el proyecto GNU

El proyecto GNU consiste en el desarrollo de un sistema operativo explícitamente libre (es decir, que viene con garantías expresas para ciertas libertades de los usuarios y los desarrolladores). Este sistema operativo está basado en Unix (que suelo escribir como *nix), pero tiene algunas diferencias, mejoras. De ahí el nombre: «GNU» significa "GNU's Not Unix" ("GNU No es Unix"). Efectivamente, se trata de un acrónimo recursivo, algo característico de la juguetona cultura hacker.

Actualmente, hay muchas variaciones del sistema operativo GNU que son utilizadas en campos tan variados como el de los servidores, el de la supercomputación y el de los ordenadores domésticos. La variante más popular, sin duda, es lo que algunos llaman GNU/Linux y, probablemente, la mayoría llama Linux. Esta variante consiste en el espacio de usuario del sistema GNU en combinación con el núcleo Linux. También podría considerarse GNU/Linux como una variante de Linux, puesto que hay sistemas operativos como Android que usan Linux, pero no usan o casi no usan GNU. Para complicar más las cosas, hay muchas distribuciones diferentes de GNU/Linux; por ejemplo, están Debian GNU/Linux y Triskel GNU/Linux. Las cosas se complican en Debian: también hay una versión de Debian llamada Debian GNU/kFreeBSD que tiene el espacio de usuario de GNU con el núcleo de FreeBSD, una versión llamada Debian GNU/NetBSD que es GNU con el núcleo de NetBSD (¡el proyecto NetBSD cumplió dos décadas esta primavera!) y una llamada Debian GNU/Hurd que tiene el espacio de usuario de GNU y el núcleo Hurd que también es de GNU.

Actualmente, GNU tiene muchos componentes propios y otros ajenos. Los componentes propios incluyen la biblioteca estándar de C (que forma junto al núcleo la base sobre la que se construye un sistema tipo *nix), herramientas de programación, herramientas de manipulación de texto y ficheros, un intérprete de línea de órdenes, un entorno de escritorio, programas de campos específicos (manipulación de imágenes, notación musical, contabilidad, estadística, cálculo numérico, diseño asistido por ordenador…) y muchas cosas más. Esto puede parecer mucho, pero es algo minúsculo frente a la cantidad de software libre que se ha desarrollado fuera del proyecto GNU durante estas décadas y que ha surgido gracias a la existencia del concepto del software libre y el empeño de unos pocos por hacer que el ser humano conserve sus derechos en el ámbito de la computación, un terreno que se hace más importante e influyente cada día que pasa. ¡Gracias!

Importancia del proyecto GNU

El lanzamiento del proyecto GNU, al iniciar el movimiento del software libre, es algo de una importancia histórica inmensa. El software libre supuso la formalización de las antiguas prácticas que se basaban en la regla de oro y la solidaridad, la respuesta a un modelo egoísta, monopolista y deshumanizador que amenazaba con eliminar toda alternativa. Hoy por hoy, el software libre es una opción real para quizá no todas las necesidades relacionadas con la informática, pero sí para la mayoría. Si nos centramos no en la influencia indirecta, sino en el caso concreto del software del proyecto GNU, vemos que tiene una fortísima presencia en servidores y supercomputadores, aunque su penetración en el mercado doméstico y de oficina es minoritaria. Si hablamos de lo que ha posibilitado el proyecto GNU, el impacto es francamente espectacular.

Categorías: Derechos, Historia, Informática

Permalink: https://sgcg.es/articulos/2013/09/27/30-aniversario-de-gnu/

Jugando con autómatas celulares (17)

2013-09-25

Hace varios artículos, planteamos un interesante proyecto: una pequeña biblioteca para construir autómatas celulares. Los autómatas celulares son unas estructuras matemáticas muy curiosas: retículos de celdas que van cambiando de un estado a otro y que pueden, a partir de reglas sencillas, exhibir complejísimos comportamientos emergentes. Como práctica, nuestra biblioteca estará hecha en Scheme R5RS y en Python 2. El enfoque es funcional porque el problema se presta mucho a ello. No nos preocuparemos tanto por hacer un código especialmente rápido como por hacerlo claro y conciso.

Dicho lo anterior, nuestra biblioteca está bien para explorar, pero estaría mejor si pudiéramos hacer que fuera un poquito más deprisa. Podemos lograr mejoras significativas sin necesidad de realizar cambios profundos en el código, sin necesidad de hacerlo largo y prolijo. No conseguiremos algo tan rápido como un programa especializado y optimizado a mano en C, pero conseguiremos una ganancia importante con poco trabajo.

Memoización

Nuestro código tiene muchos cálculos que son redundantes. Afortunadamente, casi todo el código que hemos desarrollado es referencialmente transparente, así que es perfectamente lícito almacenar en memoria los resultados de los cálculos pesados que utilizamos más de una vez. Esta táctica es conocida como «memoización» y es muy útil cuando nuestro programa tiene problemas de rendimiento, pero hay memoria de sobra. Podemos modificar nuestras funciones para hacer esto explícitamente, pero es preferible evitar tal cosa. En vez de eso, lo que vamos a hacer es extender de alguna manera nuestro lenguaje para poder aplicar la técnica de memoización a las funciones de nuestra elección. Esto es muy fácil en Scheme porque las funciones son objetos de primera clase y tenemos a nuestra disposición un sistema de macros con el que empujar los límites del lenguaje. En Python, las funciones son casi tan versátiles como en Scheme y, aunque no hay un sistema de macros, hay unos dispositivos conocidos como «decoradores» que se adaptan al uso que queremos dar.

Empezamos con Scheme. En primer lugar, vamos a crear una función con la que crear versiones con memoización de otras funciones. Las versiones memoizadas tienen una memoria asociativa que relaciona argumentos de llamadas antiguas con sus resultados, de manera que no hace falta repetir los cálculos cuando vuelven a darse los argumentos antiguos, sino que es suficiente devolver el resultado almacenado. Usamos una lista asociativa como memoria; cada celda en esta memoria es un par cuyo primer elemento (el car) es el conjunto de argumentos que sirve como clave y cuyo segundo elemento (el cdr) es el valor devuelto por la función. Vamos añadiendo elementos al principio de la memoria mediante cons y modificamos destructivamente la memoria mediante set!. Una primera versión sería así:
(define (memoise function) (let ((cache '())) (lambda arguments (let ((cached-arguments-and-results (assoc arguments cache))) (if cached-arguments-and-results (cdr cached-arguments-and-results) (let ((results (apply function arguments))) (set! cache (cons (cons arguments results) cache)) results))))))
Esta versión no funciona con funciones que devuelven múltiples valores. En Python, trabajar con funciones que devuelven múltiples valores es relativamente sencillo porque lo que se hace en realidad es devolver una tupla y hacer el equivalente al destructuring-bind de Common Lisp para recibir los valores devueltos en múltiples variables. En Scheme R5RS, en cambio, podemos devolver múltiples valores de verdad, pero su manejo se complica porque hay que usar continuaciones. Capturamos los múltiples valores devueltos mediante una función variádica que acepta todos estos valores y los mete en una lista; después, almacenamos esta lista de valores en la celda correspondiente de la memoria; finalmente, aplicamos la función values sobre la lista de valores para poder hacer una devolución de valores múltiples propia. La solución sería así:
(define (memoise function) (let ((cache '())) (lambda arguments (let ((cached-arguments-and-results (assoc arguments cache))) (if cached-arguments-and-results (apply values (cdr cached-arguments-and-results)) (call-with-values (lambda () (apply function arguments)) (lambda results (set! cache (cons (cons arguments results) cache)) (apply values results))))))))
Una vez tenemos la función, podemos probarla. Podemos computar la secuencia de Fibonacci, por ejemplo:
(define (fibonacci n) (if (< n 2) 1 (+ (fibonacci (- n 1)) (fibonacci (- n 2)))))
Esta función hace los cálculos de una forma muy ineficiente, ya que repite los mismos cálculos una y otra vez. Podemos pisarla tras su definición con una versión con memoización:
(define fibonacci (memoise fibonacci))
La nueva función es muchísimo más rápida. A cambio, por supuesto, consume memoria. Siempre podríamos inventar una versión de memoise con un mecanismo para purgar valores memorizados antiguos para acotar el consumo de memoria.

Usar la función memoise directamente puede ser una cosa algo incómoda. Sería conveniente poder definir funciones con memoización de un solo paso y sin esfuerzo adicional sobre una definición de función convencional. Da la casualidad de que podemos extender el lenguaje mediante macros, así que estamos de enhorabuena. Lo único que tenemos que hacer es capturar definiciones de funciones normales y corrientes. La solución es así de facilita:
(define-syntax define-memoised (syntax-rules () ((_ (name . arguments) body ...) (define name (memoise (lambda arguments body ...))))))
De esta manera, podemos definir la función que calcula el elemento enésimo de la sucesión de Fibonacci como si fuera una función normal:
(define-memoised (fibonacci n) (if (< n 2) 1 (+ (fibonacci (- n 1)) (fibonacci (- n 2)))))
Es así de fácil.

Ahora vamos con Python.
def memoise(function): cache = {} def memoised_function(*arguments): if arguments in cache: return cache[arguments] else: results = function(*arguments) cache[arguments] = results return results return memoised_function
La versión de Python es más corta que la de Scheme. Como los valores múltiples van en forma de tupla normal y corriente (de manera que en realidad nunca devolvemos valores múltiples, sino un único objeto que es una tupla), no hace falta hacer cosas especiales para manejarlos.

Python no tiene macros, pero podemos hacer algo casi tan compacto como usar define-memoised gracias a los decoradores. El ejemplo de la sucesión de Fibonacci se traduce a Python así:
@memoise def fibonacci(n): if n < 2: return 1 else: return fibonacci(n-1) + fibonacci(n-2)
El decorador tiene un efecto similar al que logramos mediante macros en Scheme.

Aceleración de `cyclic-cartesian-neighbourhoods`

La función cyclic-cartesian-neighbourhoods hace muchas operaciones pesadas que podemos ahorrar si disponemos de memoria suficiente. Esta función hace muchas conversiones entre índices planos e índices multidimensionales. Algunas implementaciones de Scheme nos dan resultados significativamente más rápidos si aplicamos memoización, mientras que la diferencia no es apreciable en otras. Necesitaríamos hacer una pequeña reescritura, no obstante:
(define (cyclic-cartesian-neighbourhoods cells sizes offsets) (let ((matrix (list->vector cells))) (map (lambda (indices) (map (lambda (index) (vector-ref matrix index)) indices)) (cyclic-cartesian-neighbourhood-indices sizes offsets))))
Esta función tiene la misma interfaz que la original, pero internamente es diferente. En primer lugar, realiza el acceso aleatorio a las celdas mediante un vector y no una lista para así beneficiarse de un tiempo de acceso constante; en segundo lugar, asume que disponemos de una función llamada cyclic-cartesian-neighbourhood-indices que acepta una lista de dimensiones sizes y una lista de distancias offsets, y devuelve una lista cuyos elementos son a su vez listas con los índices planos que cyclic-cartesian-neighbourhoods utilizaría para extraer los vecinos de cada celda. La función es sin duda algo complicada:
(define-memoised (cyclic-cartesian-neighbourhood-indices sizes offsets) (define (apply-one-offset index offset) (multidimensional->flat sizes (cyclic-addition sizes index offset))) (define (apply-offsets index) (map (lambda (offset) (apply-one-offset index offset)) offsets)) (let* ((total-size (fold * 1 sizes)) (flat-indices (range 0 total-size 1)) (multidimensional-indices (map (lambda (flat-index) (flat->multidimensional sizes flat-index)) flat-indices))) (map apply-offsets multidimensional-indices)))
Hacemos memoización como optimización. Los cálculos son lo bastante largos y pesados como para que la técnica sea beneficiosa.

Podemos hacer algo similar en Python. La función cyclic_cartesian_neighbourhoods queda reescrita así:
def cyclic_cartesian_neighbourhoods(cells, sizes, offsets): return map(lambda indices: tuple(map(lambda index: cells[index], indices)), cyclic_cartesian_neighbourhood_indices(sizes, offsets))
Necesitamos crear la función cyclic_cartesian_neighbourhood_indices:
@memoise def cyclic_cartesian_neighbourhood_indices(sizes, offsets): def apply_one_offset(index, offset): return multidimensional_to_flat(sizes, cyclic_addition(sizes, index, offset)) def apply_offsets(index): return tuple(map(lambda offset: apply_one_offset(index, offset), offsets)) total_size = fold(lambda a, b: a * b, 1, sizes) flat_indices = range(0, total_size, 1) multidimensional_indices = map(lambda flat_index: flat_to_multidimensional(sizes, flat_index), flat_indices) return tuple(map(apply_offsets, multidimensional_indices))
Con esto, la ganancia en rapidez se nota mucho cuando el tablero es grande.

Otros artículos de la serie

Categorías: Informática

Permalink: https://sgcg.es/articulos/2013/09/25/jugando-con-automatas-celulares-17/

Jugando con autómatas celulares (16)

2013-09-24

Hace varios artículos, planteamos un interesante proyecto: una pequeña biblioteca para construir autómatas celulares. Los autómatas celulares son unas estructuras matemáticas muy curiosas: retículos de celdas que van cambiando de un estado a otro y que pueden, a partir de reglas sencillas, exhibir complejísimos comportamientos emergentes. Como práctica, nuestra biblioteca estará hecha en Scheme R5RS y en Python 2. El enfoque es funcional porque el problema se presta mucho a ello. No nos preocuparemos tanto por hacer un código especialmente rápido como por hacerlo claro y conciso.

Hasta ahora, hemos trabajado con autómatas de primer orden. Hay autómatas celulares de orden superior en los que el estado futuro no depende únicamente del vecindario actual, sino también de estados anteriores. Para fijar ideas, nos centraremos en autómatas de segundo orden en los que el estado futuro de una celda se basa en el estado de la propia celda en la generación anterior y en el vecindario en la generación actual.

Nuestra biblioteca parece planteada para autómatas de primer orden, pero podemos usarla con autómatas de segundo orden fácilmente; simplemente, nos limitamos a modelar los estados de las celdas con listas de dos elementos: el estado actual y el estado anterior. Esta solución no es la única posible, pero de cualquier manera tenemos que conservar los estados pasados en los autómatas de orden superior. La estructura de datos que estamos usando para representar las celdas (una lista plana) y la forma de trabajar que tiene nuestra biblioteca hace que sea conveniente almacenar los estados pasados de cada celda junto al estado actual. Este esquema permite usar la maquinaria que hemos desarrollado hasta ahora con muy poco código adicional; crearemos alguna función por mera conveniencia.

Vecindarios de orden superior

Por el mismo esfuerzo que nos cuesta crear los vecindarios de segundo orden, creamos los de orden superior arbitrario. Estos vecindarios modificados contienen, para cada celda, una lista cuyo primer elemento es el vecindario original y cuyos demás elementos son los estados anteriores en orden de antigüedad creciente. La función se llamará higher-order-neighbourhoods y aceptará como argumento una función de extracción de vecindarios de primer orden de las que hemos usado hasta ahora. Nuestra higher-order-neighbourhoods ha de devolver una función de extracción de vecindarios modificada que podremos pasar con normalidad a apply-rule. En Scheme, nuestra función es así de cortita:
(define (higher-order-neighbourhoods first-order-neighbourhoods) (lambda (cells) (let ((current-state (map car cells)) (previous-states (map cdr cells))) (map cons (first-order-neighbourhoods current-state) previous-states))))
La traducción más o menos literal a Python 2 es un poquito más engorrosa:
def higher_order_neighbourhoods(first_order_neighbourhoods): def neighbourhoods_and_previous_states(cells): current_state = map(lambda cell: cell[0], cells) previous_state = map(lambda cell: cell[1:], cells) return map(lambda current, previous: tuple(current + list(previous)), first_order_neighbourhoods(current_state), previous_state) return neighbourhoods_and_previous_states
Las «listas» de Python se manejan más bien como vectores y no hay equivalentes a car, cdr y cons, así que la construcción de variables mediante map es un poco prolija y habría quedado un código un poquito más compacto con una técnica mucho más apreciada en Python, lo que se llama en inglés list comprehensions, aunque la ganancia habría sido poco significativa. De igual manera, como las funciones anónimas de Python están apenas a un pasito de ser absolutamente inútiles por limitadas, tenemos que crear una función con nombre interna, neighbourhoods_and_previous. Python no es Scheme y estos ejemplos están más pensados como una ayuda para quien no está del todo familiarizado con Scheme que como prácticas recomendables en Python.

Reglas de segundo orden

Las reglas de los autómatas de segundo orden pueden ser de muchas formas, pero vamos a centrarnos en un caso particular que se aplica a autómatas con dos estados (0 y 1, como los autómatas elementales): partimos de una regla de primer orden y aplicamos a disyunción exclusiva a su resultado y el valor de la celda en la generación anterior:

Si la regla de primer orden dice que el nuevo estado es 0:
- si el estado antiguo es 0, el nuevo estado es 0;
- si el estado antiguo es 1, el nuevo estado es 1.
Si la regla de primer orden dice que el nuevo estado es 1:
- si el estado antiguo es 0, el nuevo estado es 1;
- si el estado antiguo es 1, el nuevo estado es 0.

Esto es lo mismo que la suma módulo 2 del nuevo estado de acuerdo con la regla de primer orden y el estado anterior.

De forma análoga a como hicimos con los vecindarios, vamos a hacer una función modificadora, second-order-rule, que aceptará una regla rule de primer orden y devolverá una regla modificada y preparada para aceptar vecindarios de segundo orden como los que producen los extractores de vecindarios creados con higher-order-neighbourhoods. Naturalmente, tenemos que devolver no simplemente el próximo estado, sino una lista con el próximo estado y el estado actual (que será el estado anterior de la próxima generación). La función, que se llamará second-order-xor-rule, no tiene mucha complicacion en Scheme:
(define (second-order-xor-rule first-order-rule) (lambda (second-order-neighbourhood) (let* ((current-neighbourhood (car second-order-neighbourhood)) (previous-state (cadr second-order-neighbourhood)) (first-order-next-state (first-order-rule current-neighbourhood))) (list (modulo (+ previous-state first-order-next-state) 2) previous-state))))
La versión en Python es así:
def second_order_xor_rule(first_order_rule): def second_order_rule(second_order_neighbourhood): current_neighbourhood = second_order_neighbourhood[0] previous_state = second_order_neighbourhood[1] first_order_next_state = first_order_rule(current_neighbourhood) return ((previous_state + first_order_next_state) % 2, previous_state) return second_order_rule

Pruebas con algunas reglas de autómatas elementales

Probamos varios autómatas elementales hace unas semanas. Hoy vamos a crear resultados con reglas de segundo orden creadas a partir de las de primer orden de entonces. En todos los casos, nuestra primera generación asume un estado anterior idéntico al que tiene. Igual que en aquel artículo, mostraremos gráficamente el resultado con las primeras generaciones en la parte superior y las últimas generaciones en la parte inferior; los píxeles blancos representarán celdas de estado 0 y los píxeles negros representarán celdas de estado 1. La nomenclatura es como la de Wolfram normal, pero con una «R» tras el número de regla para indicar que se trata de una de segundo orden creada mediante la técnica de disyunción exclusiva.

Regla 90R

Podemos generar 160 generaciones a partir de una celda centrada de esta manera:
(step (second-order-xor-rule (wolfram-rule 90)) (append (repeat '(0 0) 159) '((1 1)) (repeat '(0 0) 160)) (higher-order-neighbourhoods cyclic-elementary-neighbourhoods) 160)
Para extraer solamente los estados actuales y dejar fuera los anteriores, podemos usar map:
(map (lambda (generation) (map car generation)) (step …))
El resultado, representado gráficamente, es así:

Evolución de la regla de segundo orden 90R.

Esto recuerda un poco a la aproximación del triángulo de Sierpinski que salía con la regla 90 de primer orden.

Regla 30R

Creamos 160 generaciones así:
(step (second-order-xor-rule (wolfram-rule 30)) (append (repeat '(0 0) 159) '((1 1)) (repeat '(0 0) 160)) (higher-order-neighbourhoods cyclic-elementary-neighbourhoods) 160)
Esto queda representado gráficamente de la siguiente manera:

Evolución de la regla de segundo orden 30R.

Regla 110R

Creamos 320 generaciones así:
(step (second-order-xor-rule (wolfram-rule 110)) (append (repeat '(0 0) 319) '((1 1))) (higher-order-neighbourhoods cyclic-elementary-neighbourhoods) 320)
Esto queda representado gráficamente de la siguiente manera:

Evolución de la regla de segundo orden 110R.

Regla 11R

Partimos de un estado inicial generado pseudoaleatoriamente:
(let* ((generator (uniform-generator 0)) (size 320) (initial-state (unfold (lambda (n) (= n size)) (lambda (n) (inexact->exact (round (generator)))) (lambda (n) (+ n 1)) 0))) (step (second-order-xor-rule (wolfram-rule 11)) (zip initial-state initial-state) (higher-order-neighbourhoods cyclic-elementary-neighbourhoods) size))
El resultado es mucho menos interesante que el de la regla de primer orden:

Evolución de la regla de segundo orden 11R.

Otros artículos de la serie

Categorías: Informática

Permalink: https://sgcg.es/articulos/2013/09/24/jugando-con-automatas-celulares-16/

Día de la Libertad del Software

2013-09-21

El Día de la Libertad del Software es una celebración de periodicidad anual que sirve de homenaje al software libre. Hay fiestas organizadas a lo largo y ancho del mundo.

En un mundo en el que la informatización crece día tras día, el software libre se vuelve esencial para garantizar los derechos de los ciudadanos. El software libre defiende tu libertad de usar, estudiar, modificar y compartir el software que está presente en todos los aspectos de tu vida. Como tu vida depende tanto de la informática, el software libre te devuelve el control sobre tu propia vida.

Este año es especial porque se cumplen tres décadas desde el anuncio del proyecto GNU por parte de Richard Stallman. Podemos considerar que este anuncio supuso el nacimiento formal del movimiento del software libre. Esto es notabilísimo.

Categorías: Derechos, Fechas, Informática

Permalink: https://sgcg.es/articulos/2013/09/21/dia-de-la-libertad-del-software/

Jugando con autómatas celulares (15)

2013-09-20

Hace varios artículos, planteamos un interesante proyecto: una pequeña biblioteca para construir autómatas celulares. Los autómatas celulares son unas estructuras matemáticas muy curiosas: retículos de celdas que van cambiando de un estado a otro y que pueden, a partir de reglas sencillas, exhibir complejísimos comportamientos emergentes. Como práctica, nuestra biblioteca estará hecha en Scheme R5RS y en Python 2. El enfoque es funcional porque el problema se presta mucho a ello. No nos preocuparemos tanto por hacer un código especialmente rápido como por hacerlo claro y conciso.

Hoy vamos a crear un autómata no determinista: el modelo del incendio forestal. Este autómata trata de forma muy simplificada la evolución de un bosque en el que se producen incendios. El modelo que vamos a tratar tiene muy poco valor predictivo, pero tiene cierto interés matemático. Este autómata del incendio forestal tiene las siguientes características:

es un autómata celular no determinista;
está definido en una malla cartesiana;
los estados posibles son tres: 0 (claro), 1 (árbol) y 2 (fuego).
la evolución de una celda, que es no determinista, está influenciada por el estado de la propia celda y el de su vecindario de Moore (las celdas inmediatamente en contacto tanto según líneas coordenadas como en diagonal);
un claro pasa a estar ocupado por un árbol con una probabilidad dada;
un árbol sin fuego alrededor pasa a incendiarse con una probabilidad dada;
un árbol con algún fuego en su vecindario se incendia;
un terreno incendiado pasa a convertirse en un claro.

Vamos a trabajar con una malla bidimensional cíclica porque el caso bidimensional es similar al de una superficie forestal real y ya tenemos funciones para trabajar con mallas cíclicas y que nos permiten despreocuparnos de las condiciones de contorno.

Vecindarios

Vamos a definir vecindarios para el modelo del bosque forestal bidimensional. En primer lugar, crearemos una pequeña herramienta adicional que nos servirá para determinar si algún elemento de una lista (o los elementos correspondientes de un conjunto de listas) cumplen una determinada condición. Esta función se llama any y tiene la siguiente forma:
(define (any predicate . lists) (let ((current-arguments (map car lists)) (next-arguments (map cdr lists))) (or (apply predicate current-arguments) (if (null? (car next-arguments)) #f (apply any (cons predicate next-arguments))))))
Esta definición viene a ser como la descrita en SRFI-1. primer argumento, predicate, es una función que acepta tantos argumentos como listas le pasamos a any; esta función indica si sus argumentos cumplen o no cumplen una determinada condición. Tras predicate, any acepta una cantidad arbitraria de listas que empaqueta en lists.

Python 2 ya viene con una función llamada any, pero en vez de aceptar un predicado y un conjunto de listas, acepta meramente un iterable. Nuestra biblioteca está hecha pensando en Scheme, así que vamos a hacer una versión en Python para ver cómo se traduciría. Quedaría así de forma recursiva:
def any(predicate, *lists): current_arguments = map(lambda lst: lst[0], lists) next_arguments = map(lambda lst: lst[1:], lists) return (predicate(*current_arguments) or (False if (len(next_arguments[0]) == 0) else any(predicate, *next_arguments)))
Esto no funciona muy bien en Python. Una forma iterativa de hacer lo mismo sería así:
def any(predicate, *lists): for arguments in zip(*lists): result = predicate(*arguments) if result: return result return False

Ahora ya podemos definir vecindarios para el modelo del bosque forestal bidimensional. Nuestra función se llamará cyclic-forest-fire-neighbourhoods y aceptará una lista plana de celdas cells y una lista de dimensiones sizes que contiene el largo y el ancho de nuestro dominio. Podríamos devolver simplemente para cada celda ella misma junto a su vecindario de Moore, pero en vez de eso vamos a pasar solamente la información que interesa: el estado de la propia celda y si hay celdas incendiadas alrededor. Lo hacemos así:
(define (cyclic-forest-fire-neighbourhoods cells sizes) (define (nearby-fires? neighbourhood) (any (lambda (neighbour) (= neighbour 2)) neighbourhood)) (let* ((offsets '((-1 -1) (-1 0) (-1 1) (0 -1) (0 1) (1 -1) (1 0) (1 1))) (moore-neighbourhoods (cyclic-cartesian-neighbourhoods cells sizes offsets)) (fires (map nearby-fires? moore-neighbourhoods))) (zip cells fires)))
Quedaría así en Python:
def cyclic_forest_fire_neighbourhoods(cells, sizes): def nearby_fires_p(neighbourhood): return any(lambda neighbour: neighbour == 2, neighbourhood) offsets = ((-1, -1), (-1, 0), (-1, 1), (0, -1), (0, 1), (1, -1), (1, 0), (1, 1)) moore_neighbourhoods = cyclic_cartesian_neighbourhoods(cells, sizes, offsets) fires = map(nearby_fires_p, moore_neighbourhoods) return zip(cells, fires)

Regla

La regla es fácil de crear con la función stochastic-rule.
(define (forest-fire-rule tree-probability fire-probability) (stochastic-rule `(((0 #f) ((,(- 1 tree-probability) 0) (,tree-probability 1))) ((0 #t) ((,(- 1 tree-probability) 0) (,tree-probability 1))) ((1 #f) ((,(- 1 fire-probability) 1) (,fire-probability 2))) ((1 #t) ((1 2))) ((2 #f) ((1 0))) ((2 #t) ((1 0))))))
Es así en Python:
def forest_fire_rule(tree_probability, fire_probability): return stochastic_rule({(0, False): {1 - tree_probability: 0, tree_probability: 1}, (0, True): {1 - tree_probability: 0, tree_probability: 1}, (1, False): {1 - fire_probability: 1, fire_probability: 2}, (1, True): {1: 1}, (2, False): {1: 0}, (2, True): {1: 0}})
En las opciones deterministas, nos limitamos a dar una probabilidad igual a la unidad.

Puesta a prueba

Ya podemos probar nuestro autómata del incendio forestal. Las probabilidades tendrian que ser pequeñas, sobre todo la de incendio. Vamos a ver cómo quedaría en un tablero de veinte por veinte con unas probabilidades no muy altas:
(let* ((sizes '(20 20)) (tree-probability 1e-2) (fire-probability 1e-3) (rule (wrap-with-generator (forest-fire-rule tree-probability fire-probability) (uniform-generator 0))) (initial-cells (repeat 0 (apply * sizes))) (neighbourhoods (lambda (cells) (cyclic-forest-fire-neighbourhoods cells sizes))) (display-function (lambda (cells) (translate-and-display-cartesian-2d cells sizes " ^*")))) (interactive-step rule initial-cells neighbourhoods display-function))
Esto hace que los claros aparezcan como espacios en blanco, los árboles como acentos circunflejos y los fuegos como asteriscos. Con estos parámetros, aparece un fuego a la vigésima iteración:
^^ ^ ^^ ^ ^ ^^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^^ ^^ ^ ^ ^ * ^ ^ ^ ^ ^ ^ ^^ ^ ^ ^ ^ ^ ^^ ^ ^^^^^ ^ ^ ^ ^ ^ ^^^ ^^ ^^ ^ ^ ^^
El fuego es el asterisco que aparece en el centro. En realidad, esto depende del orden de evaluación de map y este orden no está definido en Scheme (sí lo está en la función map-in-order), así que el resultado depende de la implementación.

Puede ser más vistoso un resultado más grande:

Autómata del incendio forestal. Los píxeles grises son claros, los píxeles verdes son árboles y los píxeles rojos son incendios.

Otros artículos de la serie

Categorías: Informática

Permalink: https://sgcg.es/articulos/2013/09/20/jugando-con-automatas-celulares-15/

Jugando con autómatas celulares (14)

2013-09-17

Hace varios artículos, planteamos un interesante proyecto: una pequeña biblioteca para construir autómatas celulares. Los autómatas celulares son unas estructuras matemáticas muy curiosas: retículos de celdas que van cambiando de un estado a otro y que pueden, a partir de reglas sencillas, exhibir complejísimos comportamientos emergentes. Como práctica, nuestra biblioteca estará hecha en Scheme R5RS y en Python 2. El enfoque es funcional porque el problema se presta mucho a ello. No nos preocuparemos tanto por hacer un código especialmente rápido como por hacerlo claro y conciso.

Hasta ahora, habiamos trabajado con autómatas deterministas. Hoy vamos a sofisticar un poco nuestra biblioteca para poder trabajar con autómatas no deterministas, es decir, autómatas en el que las reglas fijan no cambios que se producen siempre, sino probabilidades de cambio.

Regla no determinista

Vamos a escribir la regla no determinista como una función referencialmente transparente o pura. Solamente tenemos que suministrar números pseudoaleatorios externamente para obtener un comportamiento aparentemente no determinista; una secuencia conocida nos daría resultados trivialmente repetibles. La función generadora de reglas, stochastic-rule, acepta un argumento con una sintaxis similar a la de deterministic-rule en la que las claves son estados de los conjuntos de vecinos y los valores son, en vez de los estados próximos correspondientes, tablas que asocian probabilidades con nuevos estados. Veamos esto con un ejemplo. Supongamos que tenemos un vecindario compuesto por tres celdas (la de la izquierda, la propia celda y la de la derecha, por ejemplo) y dos estados posibles (0 y 1). El nuevo estado de la celda es el estado anterior una de cada diez veces, el complementario del estado anterior dos de cada diez veces y el producto del estado de la izquierda y el estado de la derecha siete de cada diez veces. La tabla que define esta regla es así:
'(((0 0 0) ((1/10 0) (2/10 1) (7/10 0))) ((0 0 1) ((1/10 0) (2/10 1) (7/10 0))) ((0 1 0) ((1/10 1) (2/10 0) (7/10 0))) ((0 1 1) ((1/10 1) (2/10 0) (7/10 0))) ((1 0 0) ((1/10 0) (2/10 1) (7/10 0))) ((1 0 1) ((1/10 0) (2/10 1) (7/10 1))) ((1 1 0) ((1/10 1) (2/10 0) (7/10 0))) ((1 1 1) ((1/10 1) (2/10 0) (7/10 1))))
Esta función generadora de reglas devuelve una función regla que acepta un número aleatorio random-number y una lista neighbours con los estados de los vecinos. Con un valor dado de neighbours y muchos valores de random-number distrubuidos uniformemente entre 0 y 1, la salida de la función regla tendería a seguir una distribución de Bernoulli generalizada con las probabilidades dadas. Podemos hacer esto sin más que acumular las probabilidades y coger el resultado correspondiente a la probabilidad acumulada más pequeña que supera el valor del número aleatorio. Una versión poco eficiente es así:
(define (stochastic-rule table) (lambda (random-number neighbours) (let* ((probabilities (map car (cadr (assoc neighbours table)))) (outcomes (map cadr (cadr (assoc neighbours table)))) (thresholds (cumulative-map + 0 probabilities))) (do ((threshold (car thresholds) (car remaining-thresholds)) (remaining-thresholds (cdr thresholds) (cdr remaining-thresholds)) (outcome (car outcomes) (car remaining-outcomes)) (remaining-outcomes (cdr outcomes) (cdr remaining-outcomes))) ((<= random-number threshold) outcome)))))
La versión en Python es menos densa:
def stochastic_rule(table): def rule(random_number, neighbours): probabilities, outcomes = table[neighbours].items() thresholds = cumulative_map(lambda a, b: a + b, 0, probabilities) for threshold, outcome in zip(thresholds, outcomes): if random_number <= threshold: return outcome return rule
Podemos hacer algo similar en Scheme de varias formas. La siguiente usa continuaciones:
(define (stochastic-rule table) (lambda (random-number neighbours) (call-with-current-continuation (lambda (return) (let* ((probabilities (map car (cadr (assoc neighbours table)))) (outcomes (map cadr (cadr (assoc neighbours table)))) (thresholds (cumulative-map + 0 probabilities))) (for-each (lambda (threshold outcome) (if (<= random-number threshold) (return outcome))) thresholds outcomes))))))

Hay muchas formas de utilizar las reglas no deterministas. Podríamos hacer un código funcional puro en la medida de lo posible, pero habría que crear varias funciones nuevas para pasar los números aleatorios directamente (con una pequeña generalizacion de apply-rule) o encapsular los números aleatorios en la lista de celdas o en la lista de vecinos. Vamos a seguir una alternativa más corta que no es funcional pura, pero sí parece mucho más práctica: modificar únicamente la regla para que vaya generando números aleatorios internamente. Podemos hacer una función wrap-with-generator que acepte una función de dos argumentos (como nuestra regla) y una función generadora que vaya devolviendo valores nuevos a cada invocación, valores que usar como primer argumento de la función de dos argumentos. Es así:
(define (wrap-with-generator function generator) (lambda (argument) (function (generator) argument)))
Es igual en Python:
def wrap_with_generator(function, generator): return lambda argument: function(generator(), argument)
Si tenemos un generador de números aleatorios distribuidos uniformemente entre 0 y 1, podemos usarlo con stochastic-rule y wrap-with-generator para crear una regla aleatoria.

Generación de números pseudoaleatorios

Vamos a hacer un generador de números pseudoaleatorios que funcione igual en Scheme y en Python. Hay muchos tipos de generador con méritos variados; nosotros vamos a usar uno que quizá no vale para mucho más que para dar el pego, pero tiene la ventaja de que es muy cortito.
(define (linear-congruential-generator previous multiplier increment modulus) (modulo (+ (* multiplier previous) increment) modulus))
Es así en Python:
def linear_congruential_generator(previous, multiplier, increment, modulus): return (multiplier * previous + increment) % modulus
Este generador acepta un valor anterior previous y unos parámetros multiplier, increment y modulus para generar el siguiente valor de una secuencia pseudoaleatoria. La calidad de los resultados, que no va a ser excelente, depende de los parámetros.

Vamos a crear una función que devuelve un generador de números aleatorios distribuidos uniformemente entre 0 y 1 a partir de un valor semilla seed que sirve para determinar el estado inicial. Podemos hacerlo con linear-congruential-generator y unos parámetros que dan resultados bastante decentes:
(define (uniform-generator seed) (lambda () (let ((multiplier 1103515245) (increment 12345) (modulus 2147483648)) (set! seed (linear-congruential-generator seed multiplier increment modulus)) (/ (inexact->exact seed modulus)))))
Eso era Scheme. En Python es así:
def uniform_generator(seed): memory = [seed] def generate(): multiplier = 1103515245 increment = 12345 modulus = 2147483648 memory[0] = linear_congruential_generator(memory[0], multiplier, increment, modulus) return float(memory[0]) / 2147483648 return generate
Hacer clausuras con estado mutable es un poco más complicado en Python que en Scheme, pero no es imposible.

Podemos juntar todo así para crear una regla aleatoria:
(wrap-with-generator (uniform-generator 0) (stochastic-rule '(((0 0 0) ((1/10 0) (2/10 1) (7/10 0))) ((0 0 1) ((1/10 0) (2/10 1) (7/10 0))) ((0 1 0) ((1/10 1) (2/10 0) (7/10 0))) ((0 1 1) ((1/10 1) (2/10 0) (7/10 0))) ((1 0 0) ((1/10 0) (2/10 1) (7/10 0))) ((1 0 1) ((1/10 0) (2/10 1) (7/10 1))) ((1 1 0) ((1/10 1) (2/10 0) (7/10 0))) ((1 1 1) ((1/10 1) (2/10 0) (7/10 1))))))

Otros artículos de la serie

Categorías: Informática

Permalink: https://sgcg.es/articulos/2013/09/17/jugando-con-automatas-celulares-14/

Jugando con autómatas celulares (13)

2013-09-15

Hace varios artículos, planteamos un interesante proyecto: una pequeña biblioteca para construir autómatas celulares. Los autómatas celulares son unas estructuras matemáticas muy curiosas: retículos de celdas que van cambiando de un estado a otro y que pueden, a partir de reglas sencillas, exhibir complejísimos comportamientos emergentes. Como práctica, nuestra biblioteca estará hecha en Scheme R5RS y en Python 2. El enfoque es funcional porque el problema se presta mucho a ello. No nos preocuparemos tanto por hacer un código especialmente rápido como por hacerlo claro y conciso.

Con toda la infraestructura que tenemos ya montada, podemos construir con pocas líneas uno de los autómatas más conocidos y populares: el juego de la vida de Conway. Este autómata tiene las siguientes características:

consiste en un retículo bidimensional cartesiano;
las celdas tienen dos estados posibles: 0 o muerta y 1 o viva;
el vecindario de una celda es su vecindario de Moore (las celdas que están en inmediato contacto con ella, lo que incluye contacto en diagonal) unido a la propia celda;
el próximo estado depende del valor de la propia celda y la suma de los valores del vecindario de Moore.

La última característica hace que digamos que la regla es totalista (depende de la suma de los valores del vecindario y no de los valores individuales) exterior (también depende del propio estado de la celda en cuestión). Como ya tenemos una función (deterministic-rule) que nos construye reglas deterministas a partir de una tabla que asocia conjuntos de vecinos con estados futuros, podemos reutilizarla y construir vecindarios que en realidad consisten en la suma de los estados vecinos.

Vecindarios totalistas

Podemos reutilizar la función cyclic-cartesian-neighbourhoods que ya definimos para obtener vecindarios en retículos cartesianos cíclicos; lo que hacemos es sumar los estados vecinos que devuelve y así obtenemos lo que le interesa a una regla totalista. La función que vamos a hacer, cyclic-cartesian-totalistic-neighbourhoods, acepta una lista de celdas cells, una lista de dimensiones sizes y una lista desplazamientos offsets, todo de forma análoga cyclic-cartesian-neighbourhoods. El código en Scheme es así:
(define (cyclic-cartesian-totalistic-neighbourhoods cells sizes offsets) (map (lambda (neighbourhood) (map + neighbourhood)) (cyclic-cartesian-neighbourhoods cells sizes offsets)))
El equivalente en Python es así:
def cyclic_cartesian_totalitic_neighbourhoods(cells, sizes, offsets): return map(lambda neighbourhoods: sum(neighbourhood), cyclic_cartesian_neighbourhoods(cells, sizes, offsets))

Vecindarios totalistas externos

El juego de la vida de Conway no es meramente totalista, sino totalista externo. Esto significa que tenemos que conocer no solamente la suma del vecindario, sino también el valor de la propia celda. Podemos construir un vecindario «artificial» que contiene el valor de la propia celda y el valor de la suma de las celdas vecinas que calculamos con cyclic-cartesian-totalistic-neighbourhoods. El resultado es una función de nombre tan largo:
(define (cyclic-cartesian-outer-totalistic-neighbourhoods cells sizes offsets) (zip cells (cyclic-cartesian-totalistic-neighbourhoods cells sizes offsets)))
El equivalente en Python es así:
def cyclic_cartesian_outer_totalistic_neighbourhoods(cells, sizes, offsets): return zip(cells, cyclic_cartesian_totalistic_neighbourhoods(cells, sizes, offsets))

Reglas de Conway

En el juego de la vida de Conway, una celda muerta pasa a estar viva si tiene exactamente tres celdas vecinas vivas, mientras que una celda viva continúa con vida si tiene dos o tres celdas vecinas vivas; en todos los demás casos, la celda está muerta en el siguiente turno. Podemos interpretar esto como que tres celdas (no más, no menos) en contacto con una posición pueden reproducirse en esa posición, mientras que las celdas vivas se mueren cuando están solas y sin apoyo o cuando hay superpoblación. Con la estructura de vecinos que generamos con cyclic-cartesian-outer-totalistic-neighbourhoods, podemos crear una regla determinista así:
(deterministic-rule '(((0 0) 0) ((0 1) 0) ((0 2) 0) ((0 3) 1) ((0 4) 0) ((0 5) 0) ((0 6) 0) ((0 7) 0) ((0 8) 0) ((1 0) 0) ((1 1) 0) ((1 2) 1) ((1 3) 1) ((1 4) 0) ((1 5) 0) ((1 6) 0) ((1 7) 0) ((1 8) 0)))
Esto es tan largo que es muy incómodo. Podemos escribir una función para que sea la máquina quien escriba la tabla. Ya puestos, podemos generalizar un poco el modelo. Hay reglas alternativas a la de Conway que dan resultados muy diversos. Podemos usar una notación sencilla para estas reglas en la que especificamos los números de celdas vecinas vivas que necesita una celda muerta para nacer y los números de celdas vecinas vivas que necesita una celda viva para mantenerse con vida. Definimos una función llamada generalised-conway-rule que construye la regla determinista que buscamos a partir del valor máximo maximum-sum que puede tomar la suma, la lista born de sumas que provocan nacimiento y la lista stay-alive de sumas que provocan que la celda permanezca con vida:
(define (generalised-conway-rule maximum-sum born stay-alive) (define (half-rule current-state alive-list) (map (lambda (sum) (list (list current-state sum) (if (member sum alive-list) 1 0))) (range 0 (+ maximum-sum 1) 1))) (deterministic-rule (append (half-rule 0 born) (half-rule 1 stay-alive))))
Como el número de sumas es pequeño en principio, esta técnica de generación, que tiene un coste cuadrático, es aceptable. Podemos construir la regla de Conway convencional así:
(generalised-conway-rule 8 '(3) '(2 3))
El primer argumento puede adoptar valores diferentes al empleado si definimos autómatas en más de dos dimensiones o si usamos vecindarios más amplios; en cuanto a los parámetros born y stay-alive, tienen más valores que dan lugar a comportamientos complejos. La regla (generalised-conway-rule 8 '(2) '(7)), por ejemplo, da lugar a muchas estructuras móviles.

La traducción más o menos literal del código anterior a Python 2 es así:
def generalised_conway_rule(maximum_sum, born, stay_alive): def half_rule(current_state, alive_list): return map(lambda sum: [(current_state, sum), 1 if sum in alive_list else 0], range(0, maximum_sum + 1, 1)) return deterministic_rule(dict(half_rule(0, born) + half_rule(1, stay_alive)))

El juego de la vida de Conway

Ahora podemos poner en marcha el juego de la vida de Conway. Tenemos que generar un tablero interesante. Vamos a hacer uno de 9 filas y 11 columnas con un planeador justo en el medio. Los nombres de funciones tan larguísimos que estamos usando hacen que todo sea un poco engorroso. El código es así:
(let* ((rule (generalised-conway-rule 8 '(3) '(2 3))) (initial-cells '(0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0)) (sizes '(9 11)) (ccotn cyclic-cartesian-outer-totalistic-neighbourhoods) (offsets '((-1 -1) (-1 0) (-1 1) (0 -1) (0 1) (1 -1) (1 0) (1 1))) (neighbourhoods (lambda (cells) (ccotn cells sizes offsets))) (display-function (lambda (cells) (translate-and-display-cartesian-2d cells sizes ".*")))) (interactive-step rule initial-cells neighbourhoods display-function))
Los primeros estados salen así:

........... ........... ........... .....*..... ......*.... ....***.... ........... ........... ...........
........... ........... ........... ........... ....*.*.... .....**.... .....*..... ........... ...........
........... ........... ........... ........... ......*.... ....*.*.... .....**.... ........... ...........
........... ........... ........... ........... .....*..... ......**... .....**.... ........... ...........
........... ........... ........... ........... ......*.... .......*... .....***... ........... ...........
........... ........... ........... ........... ........... .....*.*... ......**... ......*.... ...........
........... ........... ........... ........... ........... .......*... .....*.*... ......**... ...........
........... ........... ........... ........... ........... ......*.... .......**.. ......**... ...........
........... ........... ........... ........... ........... .......*... ........*.. ......***.. ...........
........... ........... ........... ........... ........... ........... ......*.*.. .......**.. .......*...
........... ........... ........... ........... ........... ........... ........*.. ......*.*.. .......**..
........... ........... ........... ........... ........... ........... .......*... ........**. .......**..
........... ........... ........... ........... ........... ........... ........*.. .........*. .......***.
........*.. ........... ........... ........... ........... ........... ........... .......*.*. ........**.
........**. ........... ........... ........... ........... ........... ........... .........*. .......*.*.
........**. ........... ........... ........... ........... ........... ........... ........*.. .........**
........*** ........... ........... ........... ........... ........... ........... .........*. ..........*
.........** .........*. ........... ........... ........... ........... ........... ........... ........*.*
........*.* .........** ........... ........... ........... ........... ........... ........... ..........*
*.........* .........** ........... ........... ........... ........... ........... ........... .........*.

Otros artículos de la serie

Categorías: Informática

Permalink: https://sgcg.es/articulos/2013/09/15/jugando-con-automatas-celulares-13/

Jugando con autómatas celulares (12)

2013-09-12

Hace varios artículos, planteamos un interesante proyecto: una pequeña biblioteca para construir autómatas celulares. Los autómatas celulares son unas estructuras matemáticas muy curiosas: retículos de celdas que van cambiando de un estado a otro y que pueden, a partir de reglas sencillas, exhibir complejísimos comportamientos emergentes. Como práctica, nuestra biblioteca estará hecha en Scheme R5RS y en Python 2. El enfoque es funcional porque el problema se presta mucho a ello. No nos preocuparemos tanto por hacer un código especialmente rápido como por hacerlo claro y conciso.

Hasta el momento, todos los ejemplos que hemos visto han sido de autómatas unidimensionales. Los autómatas unidimensionales son fáciles de visualizar. También son fáciles de visualizar los bidimensionales, aunque con la desventaja de que no podemos seguir su historia de un vistazo en una pantalla bidimensional como sí podemos hacer con los unidimensionales. Hoy vamos a preparar una función para imprimirlos por pantalla cómodamente. Nos centraremos en autómatas definidos en un retículo cartesiano; dejamos fuera otras construcciones más complicadas como pueden ser los retículos hexagonales o de panal de abeja.

Conversión de listas planas en listas de listas

Resulta muy conveniente convertir la representación de lista plana de un retículo cartesiano bidimensional en una lista cuyos elementos son a su vez listas, cada una con una fila del retículo. Podemos hacer el trabajo de forma muy compacta con ayuda de las funciones que ya hemos diseñado en entregas anteriores. En Scheme, el código es así:
(define (cartesian-rows cells sizes) (let ((rows (car sizes)) (columns (cdr sizes))) (map (lambda (row) (map (lambda (column) (matrix-ref cells sizes (list row column))) (range 0 columns 1))) (range 0 rows 1))))
La función cartesian-rows acepta una lista plana de celdas cells y una lista de dimensiones sizes que contiene el número de filas y el número de columnas. La traducción esencialmente literal a Python es así:
def cartesian_rows(cells, sizes): rows, columns = sizes return map(lambda row: map(lambda column: matrix_ref(cells, sizes, (row, column)), range(0, columns, 1)), range(0, rows, 1))

Impresión por pantalla de retículos cartesianos bidimensionales

Vamos a reutilizar la función translate-and-display-1d. La nueva función, translate-and-display-cartesian-2d, convierte su argumento cells (una lista plana de celdas que representa un retículo bidimensional) junto con el segundo argumento sizes (una lista de dimensiones con el número de filas y el número de columnas) para obtener una lista de filas con cartesian-rows; posteriormente, recorre esta lista de filas y hace llamadas sucesivas a translate-and-display-1d con la tabla de traducción translation-table (que es una cadena de caracteres que sirve para asignar los números de los estados de las celdas a los caracteres en las posiciones correspondientes de la cadena). Quizá queda más claro el código en Scheme:
(define (translate-and-display-cartesian-2d cells sizes translation-table) (for-each (lambda (row) (translate-and-display-1d row translation-table) (newline)) (cartesian-rows cells sizes)))
La traducción a Python también es inmediata:
def translate_and_display_cartesian_2d(cells, sizes, translation_table): import sys for row in cartesian_rows(cells, sizes): translate_and_display_1d(row, translation_table) sys.stdout.write('\n')

Veamos un ejemplo del código anterior:
(translate-and-display-cartesian-2d '(0 0 1 0 0 1 0 0 1 0 0 0 0 0 0 1 0 1 0 0) '(5 4) " *")
La salida es así:
* * * * *

Otros artículos de la serie

Categorías: Informática

Permalink: https://sgcg.es/articulos/2013/09/12/jugando-con-automatas-celulares-12/

Jugando con autómatas celulares (11)

2013-09-08

Hace varios artículos, planteamos un interesante proyecto: una pequeña biblioteca para construir autómatas celulares. Los autómatas celulares son unas estructuras matemáticas muy curiosas: retículos de celdas que van cambiando de un estado a otro y que pueden, a partir de reglas sencillas, exhibir complejísimos comportamientos emergentes. Como práctica, nuestra biblioteca estará hecha en Scheme R5RS y en Python 2. El enfoque es funcional porque el problema se presta mucho a ello. No nos preocuparemos tanto por hacer un código especialmente rápido como por hacerlo claro y conciso.

Tenemos una biblioteca de autómatas celulares que empieza a ser muy potente. ¡Probemos unos pocos autómatas elementales!

Regla 90

Vamos a repetir el experimento de la regla 90 que hicimos en el segundo artículo de la serie. Partiremos, como aquella vez, de una celda activa (de estado 1) centrada y rodeada de celdas inactivas; imprimiremos asteriscos para mostrar celdas activas y espacios en blanco para mostrar celdas inactivas. El código es así:
(interactive-step (wolfram-rule 90) (append (repeat 0 10) (list 1) (repeat 0 10)) cyclic-elementary-neighbourhoods (lambda (cells) (translate-and-display-1d cells " *")))
Esto es en Scheme. En Python, es así:
interactive_step(wolfram_rule(90), [0] * 10 + [1] + [0] * 10, cyclic_elementary_neighbourhoods, lambda cells: translate_and_display_1d(cells, " *"))
En cualquiera de los dos casos, tras unas cuantas iteraciones, reproducimos una forma que recuerda a un triángulo de Sierpinski. Es como si hubiéramos llegado al final del fractal en un mundo discreto y a partir de allí, de una esquinita, nos alejáramos más y más. Las primeras líneas tienen este aspecto:
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
Esto tiene la siguiente pinta visto desde lejos:

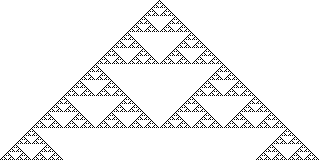
Ejemplo de evolución mediante la regla 90.

Regla 30

La regla 30 produce hermosos resultados de apariencia aleatoria. Si partimos, como antes, de un punto central,
(interactive-step (wolfram-rule 30) (append (repeat 0 10) (list 1) (repeat 0 10)) cyclic-elementary-neighbourhoods (lambda (cells) (translate-and-display-1d cells " *"))),
el resultado no es muy impresionante:
* *** ** * ** **** ** * * ** **** *** ** * * * ** **** ****** ** * *** * ** **** ** * *** ** * * **** ** *
Esto es muy pequeño. La siguiente imagen tiene más líneas:

Ejemplo de evolución mediante la regla 30.

Regla 110

En la regla 110, el estado de la celda a la derecha es ignorado. Podemos probar con una celda encendida en el punto situado más a la derecha:
(interactive-step (wolfram-rule 110) (append (repeat 0 19) (list 1)) cyclic-elementary-neighbourhoods (lambda (cells) (translate-and-display-1d cells " *")))

Las primeras generaciones salen así:
* ** *** ** * ***** ** * *** ** ** * *** ******* * ** *** *** ** * ** * ***** ***** ** * ** * *** ** *** **** * *** ** * ** ***** * ******** ** *** ** **** ** * *** ** * ***** ** * *** **** *
Visto desde más lejos, tenemos el siguiente resultado:

Ejemplo de evolución mediante la regla 110.

Regla 11

Esta regla da lugar a patrones ondulatorios que avanzan hacia la derecha como ondas planas. La siguiente imagen muestra el resultado a partir de un estado inicial aleatorio:

Ejemplo de evolución mediante la regla 11.

Otros artículos de la serie

Categorías: Informática

Permalink: https://sgcg.es/articulos/2013/09/08/jugando-con-automatas-celulares-11/

Jugando con autómatas celulares (10)

2013-09-02

Hace varios artículos, planteamos un interesante proyecto: una pequeña biblioteca para construir autómatas celulares. Los autómatas celulares son unas estructuras matemáticas muy curiosas: retículos de celdas que van cambiando de un estado a otro y que pueden, a partir de reglas sencillas, exhibir complejísimos comportamientos emergentes. Como práctica, nuestra biblioteca estará hecha en Scheme R5RS y en Python 2. El enfoque es funcional porque el problema se presta mucho a ello. No nos preocuparemos tanto por hacer un código especialmente rápido como por hacerlo claro y conciso.

Seguimos construyendo funciones para hacer una biblioteca de autómatas celulares razonablemente general y práctica. El trabajo de hoy nos permitirán crear muchas generaciones sucesivas de nuestros autómatas cómodamente.

Bucle interactivo

Podemos generalizar lo que hicimos con la función interactive-rule-90 del segundo artículo de la serie. Vamos a crear una función llamada interactive-step que aceptará la regla rule a aplicar, una lista cells de celdas, una función neighbourhoods con la que extraer los vecindarios y una función display-cells con la que mostrar por pantalla las celdas. Esta función es así en Scheme:
(define (interactive-step rule cells neighbourhoods display-cells) (display-cells cells) (if (not (equal? (read-char) #\q)) (interactive-step rule (apply-rule rule cells neighbourhoods) neighbourhoods display-cells)))

El parámetro display-cells puede ser display simplemente o, mejor, una llamada a translate-and-display-1d, esta función que aceptaba una cadena translation-table que permitía traducir los números de estado a caracteres mediante la función translate; estas funciones de traducción fueron definidas hace varios artículos.

La versión de Python es similar, pero en vez de usar recursión final, usamos un bucle. El código es así:
def interactive_step(rule, cells, neighbourhoods, display_cells): import sys display_cells(cells) while not sys.stdin.readline()[0] is 'q': new_cells = apply_rule(rule, cells, neighbourhoods) cells = new_cells display_cells(cells)

Bucle no interactivo

También podemos querer iterar el autómata cierto número de generaciones. Recogeremos las generaciones en una lista para su posterior inspección y manipulación. Esta vez, usaremos un bucle do explícito en vez de nuestras construcciones funcionales habituales. El trabajo con unfold en este caso sería algo engorroso debido a que habría que empaquetar los argumentos o, como alternativa, a definir algún elemento no estrictamente funcional como una función que mediante clausura fuera haciendo descender un contador interno. Esta versión tan concisa hace la magia:
(define (step rule cells neighbourhoods number-of-generations) (do ((current-cells cells (apply-rule rule current-cells neighbourhoods)) (generations-so-far '() (cons current-cells generations-so-far)) (generations-left number-of-generations (- generations-left 1))) ((< generations-left 1) (reverse generations-so-far))))
Acepta una función regla rule, una lista de celdas inicial cells, una función de extracción de vecindarios neighbourhoods y el número number-of-generations de generaciones que crear. La salida es una lista cuyos elementos son las listas de celdas de las diferentes generaciones desde la primera hasta la última.

El código de Python hace algo similar, pero con la lista de generaciones creada desde el principio. El resultado es el mismo. El código es el siguiente:
def step(rule, cells, neighbourhoods, number_of_generations): generations_so_far = [] * number_of_generations generations_so_far[0] = cells for generation_number in range(1, number_of_generations, 1): current_cells = generations_so_far[generation_number-1] generations_so_far[generation_number] = apply_rule(rule, current_cells, neighbourhoods) return generations_so_far

Otros artículos de la serie

Categorías: Informática

Permalink: https://sgcg.es/articulos/2013/09/02/jugando-con-automatas-celulares-10/