Enero de 2015
Calendario de artículos de de 2015
| lu | ma | mi | ju | vi | sá | do |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | |
Campeonato de Europa de Patinaje Artístico de 2015 (4)
2015-01-31
Esta semana se celebra el Campeonato de Europa de Patinaje Artístico de 2015. Hoy ha tenido lugar el largo femenino.
La española Sonia Lafuente ha mejorado un poco su resultado del programa corto hasta situarse en la posición número 18.
Las tres primeras plazas han quedado en manos de las tres rusas participantes, como ya esperábamos. El «combate» entre Elizaveta Tuktamysheva y Elena Radionova ha estado efectivamente reñido y se han invertido las posiciones que habían quedado tras el corto por un margen minúsculo: Tuktamysheva, con un programa impoluto, se ha llevado el oro, mientras que Radionova, con un programa ligerísimamente más ambicioso pero menos brillante en su ejecución, ha conseguido la plata. Anna Pogorilaya ha quedado en tercer lugar.
Mañana será la final de parejas.
Categorías: Actualidad, Deporte
Permalink: https://sgcg.es/articulos/2015/01/31/campeonato-de-europa-de-patinaje-artistico-4/
Campeonato de Europa de Patinaje Artístico de 2015 (3)
2015-01-30
Esta semana se celebra el Campeonato de Europa de Patinaje Artístico de 2015. Hoy han tenido lugar el corto de parejas y el largo de danza.
- En parejas, tenemos un dominio rotundo por parte de Rusia. Ksenia Stolbova y Fedor Klimov se sitúan primeros con menos de un par de puntos de ventaja sobre los segundos, Yuko Kavaguti y Alexander Smnirnov. A casi 10 puntos de distancia se sitúan los franceses Vanessa James y Morgan Cipres, terceros, que no andan demasiado lejos de las siguientes dos parejas. Mucho tienen que torcerse las cosas para que no tengamos un juego de dos categorías en una: la que compite por el oro y la que compite por el bronce.
- En la categoría masculina, Javier Fernández renueva su título de campeón de Europa. Ya van tres oros seguidos. El programa tuvo algunos accidentes (el cuádruple salchow fallido y las dos últimas combinaciones a medio gas…), pero fue en los demás elementos consistentemente el más limpio de la jornada. Rusia se llevó los dos siguientes puestos: el segundo para un Maxim Kovtun que ascendió bien desde su cuarto puesto del corto y le robó la plaza por un par de puntos a Sergei Voronov, que quedó tercero. Una lástima el largo del checo Michal Brezina, que se estrelló hasta la quinta plaza final (con el séptimo mejor largo) desde su tercera plaza del corto. No nos olvidamos del español Javier Raya, que hizo un trabajo muy satisfactorio y subió al puesto 14 desde el 21 en el que había quedado tras el corto; este resultado es el mejor que ha obtenido en un Europe.
Mañana será la final femenina.
Categorías: Actualidad, Deporte
Permalink: https://sgcg.es/articulos/2015/01/30/campeonato-de-europa-de-patinaje-artistico-3/
Campeonato de Europa de Patinaje Artístico de 2015 (2)
2015-01-29
Esta semana se celebra el Campeonato de Europa de Patinaje Artístico de 2015. Hoy han tenido lugar el corto femenino y el largo de danza.
- En la categoría femenina, la española Sonia Lafuente ha alcanzado la plaza número 20, con lo que queda clasificada para la final. Rusa copa el podio temporal con Anna Pogorilaya en el tercer puesto, Elizaveta Tuktamysheva en el segundo puesto y Elena Radionova en el primer puesto. Las dos primeras están muy fuertes y peligrosamente próximas entre sí; podría suceder cualquier cosa en el largo.
- En danza, Sara Hurtado y Adrià Díaz han estado tremendísimos y han presentado el cuarto mejor largo, lo que les ha permitido subir del sexto puesto del corto hasta la quinta plaza final. Los rusos Elena Ilinykh y Ruslan Zhiganshin, segundos tras el corto, han bajado hasta la cuarta plaza al presentar el octavo mejor largo, con desperdicio en la elevación. Los también rusos Alexandra Stepanova e Ivan Bukin han aprovechado para hacerse un hueco en el podio y subir de la cuarta plaza a la tercera. En los dos primeros puestos no ha habido sorpresas: Italia vuelve con la plata de Anna Cappellini y Luca Lanotte y Francia se lleva el oro de Gabriella Papadakis y Guillaume Cizeron.
Mañana vendrán el corto de parejas y el largo de chicos.
Categorías: Actualidad, Deporte
Permalink: https://sgcg.es/articulos/2015/01/29/campeonato-de-europa-de-patinaje-artistico-2/
Campeonato de Europa de Patinaje Artístico de 2015 (1)
2015-01-28
Esta semana se celebra el Campeonato de Europa de Patinaje Artístico de 2015. España participa en las siguientes categorías:
- Danza
- con dos parejas: los ya curtidos Sara Hurtado y Adrià Díaz y los debutantes en los Europeos Celia Robledo y Luis Fenero.
- Individual femenino
- con Sonia Lafuente.
- Individual masculino
- con los dos Javieres: Javier Fernández (que viene a defender su título de campeón de Europa un año más) y el Javier Raya.
Hoy tuvieron lugar los cortos de chicos y de danza.
- En la categoría masculina, súper Javier Fernández se sitúa en el primer puesto. Le siguen el ruso Sergei Voronov y el checo Michal Brezina, próximos entre sí. Ojo con el checo, peligrosísimo, que cometió un error importante, pero que apuntaba alto. Javier Raya acabó en el puesto 21.
- En danza, Sara Hurtado y Adrià Díaz no paran de subir; han quedado en el sexto puesto, pero rozando el quinto. Celia Robledo y Luis Fenero no han pasado el corte por un par de puestos, lamentablemente. El oro temporal se lo llevan, como era de esperar, los franceses Gabriella Papadakis y Guillaume Cizeron. La plata y el bronce, disputadísimos, quedan en manos de los rusos Elena Ilinykh y Ruslan Zhiganshin y de los italianos Anna Cappellini y Luca Lanotte. ¡El largo será muy interesante!
Mañana seguirá la competición con el corto femenino y el largo de danza.
Categorías: Actualidad, Deporte
Permalink: https://sgcg.es/articulos/2015/01/28/campeonato-de-europa-de-patinaje-artistico-1/
Diseño de una estantería librería (4)
2015-01-24
Continuamos con el diseño de una estantería librería. Ya dimensionamos las baldas a flexión y determinamos que que el conjunto básico no es satisfactoriamente estable sin anclarlo o añadir algún elemento rigidizador. Hoy vamos a aprovechar cierto espacio extra disponible para añadir unas baldas pequeñas y estabilizar la estantería al hacerlo.

Dimensiones aproximadas del espacio disponible para la estantería.
La estantería iba a ser de unos 80 cm porque tal era el ancho disponible sobre un aparador. Como se ve en la figura, a la derecha hay una vitrina y a la izquierda hay un abismo: un espacio de 20 cm de ancho entre el mueble aparador y la pared. Este espacio iba a quedar desaprovechado, pero podemos usarlo para almacenar objetos ligeros como cajas de películas. Con 21 cm de altura utilizable entre niveles, nos quedan 8 baldas que pueden guardar más de un centenar de películas. La solución es la del siguiente dos vistas:
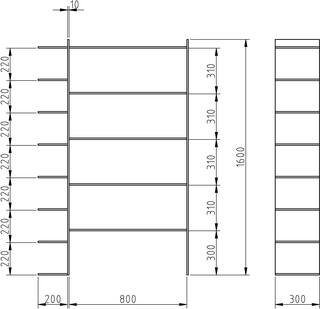
Dimensiones (en milímetros) de la estantería con las baldas
laterales.
Habíamos planteado la estantería para cortarla de un tablero grande de aglomerado. El corte inicial daba para 8 baldas de 80 cm, pero solamente habíamos usado 5. Si cogemos 2 de las 3 sobrantes y cortamos cada una en 4 tramos de 20 cm, nos salen las 8 baldas pequeñas laterales que necesitábamos.
Las baldas acaban pegando contra la pared tras poner un poco de fieltro en los cantos. Esto inmoviliza el modo de pandeo lateral que vimos ayer. La carga crítica de pandeo aumenta notablemente hasta el punto de hacerse tan grande que se convierte en una mera entelequia matemática, ya que las baldas fallarán con total seguridad antes de que la estantería se desestabilice. Como la vitrina bloquea el vuelco hacia la derecha y las baldas pequeñas laterales bloquean el vuelco hacia la izquierda, solamente son posibles los modos de pandeo más locales. Podemos acotar la carga crítica de pandeo con la del tramo vertical más largo sin apoyos: el de 30 cm de la derecha, que si fuera una mera columna con extremos montados con bisagras, tendría una carga crítica de pandeo igual a
P = E b h3 π2 ⁄ (12 L2), con
- E ≡ módulo elástico del aglomerado = 1 cm;
- b ≡ profundidad de los paneles = 30 cm;
- h ≡ espesor de los paneles = 1 cm;
- L ≡ longitud del tramo = 30 cm.
Esto es más de 4,7 kN, lo que sería montar 95 kg en cada una de las 5 baldas de 80 cm de algún modo que provocara que todo el peso fuera al panel vertical de la derecha. La estantería es ahora bastante estable.
Categorías: DIY
Permalink: https://sgcg.es/articulos/2015/01/24/diseno-de-una-estanteria-libreria-4/
Diseño de una estantería librería (3)
2015-01-23
Esta semana empezamos a ver el diseño de una estantería librería hecha con tableros de aglomerado de densidad media. Tenemos las baldas dimensionadas a flexión estática, pero todavía hay que ver si la estructura completa es razonablemente estable o puede pandear bajo cargas pequeñas. El objetivo es poder montar la estantería sin necesidad de anclarla a la pared.
Calculamos las baldas a flexión como si estuvieran simplemente apoyadas: libres de rotar en sus extremos, como si estuvieran montadas sobre bisagras. Si esto fuera así, la estructura sería un mecanismo inestable como el de la siguiente figura:
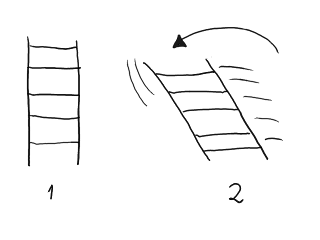
Pandeo de una estantería con uniones perfectamente flexibles a
rotación.
Las baldas irán atornilladas a escuadras. Estas uniones pueden ser muy flexibles frente a movimientos pequeños, pero cuando la estantería se inclina hacia un lado lo suficiente, los cantos de las baldas pegan contra los paneles verticales y ya no pueden rotar libremente, con lo que las baldas tienden a salir entonces aproximadamente perpendiculares. En ese momento, la estructura se rigidiza repentinamente y ya necesita un peso importante para pandear.
No buscamos mucha precisión en la predicción del pandeo de la estantería, así que podemos permitirnos hacer un cálculo aproximado mediante el método de Rayleigh con un modo asumido con buena pinta. El de la figura siguiente puede servir:
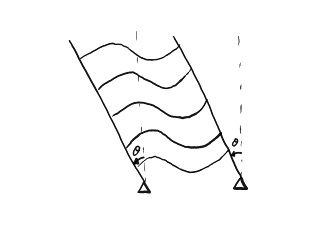
Modo de pandeo asumido.
En este modo asumido, los paneles verticales no se doblan, sino que rotan como si estuvieran articulados con el suelo mediante bisagras. Esto no es del todo descabellado de asumir cuando las rotaciones todavía no son muy grandes, ya que la fricción impide que el canto del panel deslice contra el suelo, pero no hace nada contra la rotación. Las baldas, como vimos antes, salen aproximadamente perpendiculares a los paneles verticales. Está claro que este modo no es muy realista, ya que el momento flector necesario para forzar la perpendicularidad de las baldas tendría que doblar los paneles verticales, pero sirve para un cálculo inicial rápido que indicará una cota superior y el orden de magnitud de la carga crítica de pandeo. Matemáticamente, asumimos la siguiente forma para la elástica de una balda cualquiera cuando la rotación de los paneles verticales es la θ:
w(x) ≡ θ [l ⁄ (2 π)] sin(2 π x ⁄ l).

Detalle del modo asumido para las baldas.
La balda con esta elástica almacena cierta energía potencial:
Ubalda = ∫0≤x≤l(1 ⁄ ) E (b h3 ⁄ 12) [w''(x)]2 dx = π2 E b h θ2 ⁄ (12 l),
con
- E ≡ módulo elástico del aglomerado de densidad media = 1,7 GPa;
- b ≡ profundidad de la balda = 30 cm;
- h ≡ espesor de la balda = 1 cm;
Como tenemos N baldas, la energía potencial elástica es
U = N Ubalda.
El número de baldas es N = 5.
La altura entre niveles es L = 30 cm, así que el nivel n-ésimo desciende una distancia
d(n) = n L [1 − cos(θ)] ≈ n L θ2 ⁄ 2.

Descenso de un nivel debido a la rotación.
Cada balda aguanta un peso W. Como la rotación de los tableros provoca un pequeño descenso d(n) de cada nivel, el peso n-ésimo realiza un trabajo que es
Vn = W d(n) = W L n θ2 ⁄ 2.
El trabajo total es
∑1≤n≤NVn = W L N (N+1) θ2 ⁄ 4.
En el pandeo, la energía elástica iguala al trabajo:
U = V.
Esto es lo mismo que decir
π2 N E b h θ2 ⁄ (12 l) = W L N (N+1) θ2 ⁄ 4.
El peso por balda crítico de pandeo es, por lo tanto,
W = π2 E b h ⁄ [3 (N+1) l L].
Con los números que hemos manejado, W ≈ 1,2 kN. Hay que recordar que este modo asumido es quizá poco realista y, en realidad, la carga crítica de pandeo es menor. Rehice los cálculos con el método de Rayleigh-Ritz y más términos; parece que el resultado converge a W ≈ 400 N, es decir, a lo que es colocar 40 kg de libros por balda. Aunque es difícil colocar más de 30 kg de libros en una balda, el margen es tan pequeño que resulta incómodo. Hay que buscar una solución. Sin llegar a anclar la estantería a la pared, las soluciones típicas pasan por fijar un panel trasero o por rigidizar el pie de la estantería para impedir que rote libremente. Afortunadamente, veremos que hay una muy conveniente en este caso.
Categorías: DIY
Permalink: https://sgcg.es/articulos/2015/01/23/diseno-de-una-estanteria-libreria-3/
Diseño de una estantería librería (2)
2015-01-21
Ayer planteamos el proyecto de diseñar y construir estantería para colocar libros. Entonces establecimos las dimensiones básicas de la estantería; hoy dimensionaremos las baldas.
Los tableros de aglomerado vienen en varios espesores diferentes. Interesa escoger el espesor más pequeño que garantice la correcta resistencia de la estructura, ya que los tableros delgados son más baratos y ligeros que los gruesos. Anticipamos que una balda típica trabaja más que nada como una viga simplemente apoyada en sus extremos y cargada a flexión.
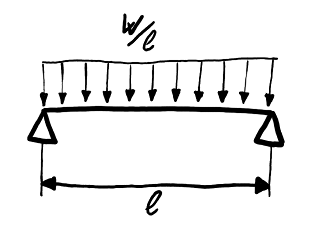
Esquema del modelo de la balda: una viga simplemente apoyada con
carga uniforme.
La balda tiene una luz l = 80 cm y sobre ella reposa un peso W uniformemente distribuido. Las tensiones dimensionantes son las que equilibran el momento flector en la sección central: M = W l ⁄ 8.
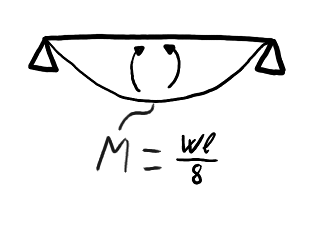
Distribución del momento flector a lo largo de la balda.
Antes de que el aglomerado empiece a romperse, aparecen esfuerzos de tracción y compresión que equilibran el momento flector como en la figura siguiente:
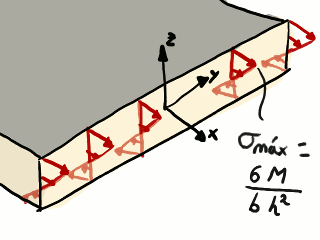
Distribución de esfuerzos en la sección central de la balda.
Ahora nos centraremos en la sección transversal de la balda, que tiene una profundidad o ancho b = 30 cm y un espesor h que es nuestra variable de diseño.
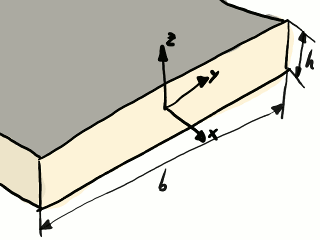
Geometría de la sección transversal de la balda.
El esfuerzo máximo es σmáx = 6 M ⁄ (b h2). Es fácil comprobar que el momento de esta distribución lineal equilibra el momento flector:
∫−b⁄2≤y≤b⁄2dy ∫−h⁄2≤z≤h⁄2dz σmáx ⋅ (2 z ⁄ h) = M.
La balda empieza a fallar en las fibras más extremas cuando se alcanza la resistencia a la flexión del material, σr, que para un aglomerado de densidad media ronda los 12 MPa. El peso máximo que puede soportar la balda sale de sustituir variables:
W = (4 ⁄ 3) (b h2 ⁄ l) σr.
Esto ya duplica el máximo peso esperado de unos 300 N con un espesor h = 1 cm. Por lo tanto, parece razonable salir adelante con este espesor, al menos por lo que se refiere a la resistencia de las baldas.
Categorías: DIY
Permalink: https://sgcg.es/articulos/2015/01/21/diseno-de-una-estanteria-libreria-2/
Diseño de una estantería librería
2015-01-20
Había que aprovechar el espacio disponible sobre un mueble bajo para colocar una librería. Aquí queda documentado el proceso de diseño y fabricación. Hoy veremos el diseño básico.
El mueble que sirve de base deja un espacio libre de algo más de 80 cm de ancho, unos 180 cm de alto y unos 40 cm de profundidad. Una librería típica necesita solamente unos 30 cm de profundidad, mientras que 80 cm de ancho dan para unas baldas generosas y los 180 cm de alto dan para unos cuantos niveles de unos 30 cm de altura, que es algo razonable para colocar cómodamente una gran variedad de libros. Las dimensiones aproximadas son las siguientes:
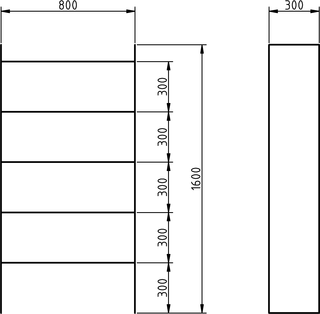
Alzado y perfil con las dimensiones aproximadas (en milímetros) de
la librería.
La balda superior está demasiado alta para ser cómoda de usar con libros, pero sirve para almacenar bultos de infrecuente utilización. No hay balda al nivel más bajo porque se aprovecha la superficie del mueble sobre la que va montada la estantería.
Una de las opciones más económicas para fabricar una librería de estas características consiste en partir de un tablero grande de aglomerado y cortarlo en las piezas necesarias. Encontramos tableros disponibles de algo más de 240 cm por algo más de 120 cm. Estas dimensiones permiten hacer la librería con unos pocos cortes: tres cortes a lo largo para dejar tablas de 30 cm y dos o tres cortes a lo ancho para dejar ocho tablas de 80 cm y dos de 160 cm. La siguiente figura ilustra los cortes:
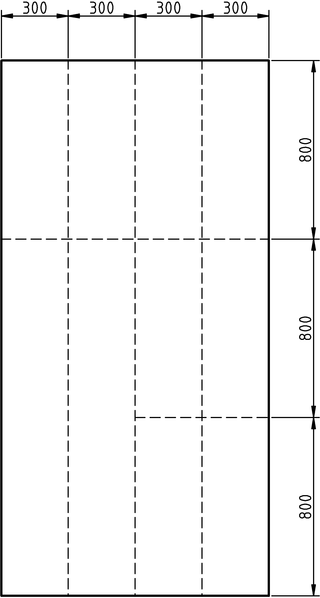
Cortes para sacar las tablas de la librería. Las dimensiones
están dadas en milímetros.
Las tablas largas de 160 cm van verticales y no llegan hasta el techo, pero permiten sujetar cualquier bulto práctico que vaya en la balda superior.
Hay tableros de varios espesores diferentes y varias opciones para fijar las baldas. Los próximos artículos servirán para hacer un dimensionado frente a cargas que permitirá construir una estantería barata y eficaz.
Categorías: DIY
Permalink: https://sgcg.es/articulos/2015/01/20/diseno-de-una-estanteria-libreria-1/
Falsa alarma por fuga de amoníaco en la Estación Espacial Internacional
2015-01-14
Hoy experimentamos una falsa alarma en la Estación Espacial Internacional. Varios indicadores telemétricos (entre ellos, un aumento en el nivel del bucle de agua del sistema de control térmico seguida de un aumento en la presión de cabina en el Node 2) eran compatibles con una fuga de amoníaco del sistema de control térmico en el segmento estadounidense. Ante la posibilidad de que se hubiera producido, de hecho, tal fuga, la tripulación se refugió en el segmento ruso mientras el equipo de control de vuelo se ocupaba en tierra de determinar la naturaleza precisa de la situación. Las operaciones científicas quedaron interrumpidas y algunos sistemas fueron desconectados como medida de precaución. No se encuentra evidencia de amoníaco en el aire y parece que las medidas que llevaron a la alarma fueron erróneas, quizá no por un problema con los sensores, sino en algún equipo intermedio.
Categorías: Actualidad, Aeroespacio
Modelando la influencia del tamaño del pecho en las molestias al correr y saltar
2015-01-12
Varios divulgadores científicos han propuesto escribir articulillos eso, divulgativos, relacionados con el busto humano: el desafío #lunesTetas. Aquí va mi aportación.
Occidente adora la estética del pecho femenino, pero las poseedoras de un busto generoso saben que estas cosas tienen sus inconvenientes al correr y saltar sin una sujeción adecuada. Vamos a plantear un modelo físico elemental (lo que en inglés se conoce como «toy model») para hacernos una idea cualitativa de cómo podrían comportarse las molestias durante la actividad física en función del tamaño del pecho.
Modelo elemental
El pecho de una mujer se comporta como un sólido viscoelástico. Muestra tendencia a recuperar su forma, pero esta fuerza de recuperación depende del ritmo de deformación. Hay múltiples maneras de modelar este comportamiento, pero una de las más sencillas (aunque con ciertas limitaciones) consiste en colapsar todo el movimiento en una sola variable, el desplazamiento x(t) de un punto representativo en función del tiempo t, y asumir que la fuerza de recuperación es la suma de una elástica lineal (como un muelle) y una de amortiguamiento viscoso también lineal (como un amortiguador). El desplazamiento está medido con respecto al tórax, que experimenta un movimiento oscilatorio con una aceleración a(t). Este modelo pierde validez rápidamente en diversas circunstancias, entre las que se incluyen los movimientos especialmente amplios y pendulares, en los que aparecen fenómenos no lineales importantes.
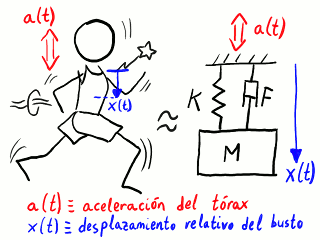
Oscilador armónico amortiguado con excitación en la base como
modelo del desplazamiento del busto al correr.
Este oscilador armónico tiene:
- una rigidez K que relaciona linealmente la fuerza de recuperación elástica (que se opone al desplazamiento del pecho y tiende a colocarlo en una posición neutral) con el desplazamiento;
- un amortiguamiento F que relaciona linealmente la fuerza de amortiguamiento (que se opone a la velocidad de deformación del pecho y tiende a frenarlo) con la rapidez del desplazamiento;
- una masa M, la inercia del pecho.
La ecuación diferencial es la siguiente:
M (d2⁄dt2) x(t) + F (d⁄dt) x(t) + K x(t) = −M a(t).
Introducimos unas variables adicionales:
- la pulsación natural ω0 ≡ √(K ⁄ M);
- el factor de amortiguamiento ζ ≡ F ⁄ (2 M ω0).
Con estas nuevas variables, tras dividir por la masa M, la ecuación diferencial queda así:
(d2⁄dt2) x(t) + 2 ζ ω0 (d⁄dt) x(t) + ω02 x(t) = −a(t).
Representación fasorial
Vamos a asumir que la aceleración sigue una ley sinusoidal periódica de pulsación ω. Usaremos el viejo truco de expresarla como una exponencial compleja (lo que se conoce como una representación fasorial); siempre podemos descartar la parte imaginaria al final:
a(t) ≡ A ei ω t.
Para fijar el origen de fase, la amplitud A es un número real.
Tras mantener la actividad durante mucho tiempo, la respuesta transitoria no se nota y solamente tenemos una respuesta que también es sinusoidal de la misma frecuencia que la excitación:
x(t) ≡ X ei ω t.
Esta formulación permitirá transformar la ecuación diferencial en una ecuación algebraica. La amplitud de la respuesta X es en general un número complejo cuyo argumento es el desfase frente a la entrada.
La ecuación diferencial queda de la siguiente manera tras introducir las formas funcionales de arriba:
(−ω2 + 2 i ζ ω0 ω + ω02) X ei ω t = −A ei ω t.
La amplitud compleja de la respuesta sale de despejar:
X = −A ⁄ (ω02 − ω2 + 2 i ζ ω0 ω).
Vamos a asumir que las molestias que experimenta nuestra atleta son directamente proporcionales a la fuerza de reacción mientras su pecho rebota. En este modelo de juguete, la fuerza de reacción es igual a la suma de la fuerza de recuperación elástica y la fuerza de amortiguamiento viscoso. De nuevo con el truco algebraico de antes, a sabiendas de que la reacción también será sinusoidal de la misma frecuencia, la amplitud compleja es
R = K X + i ω F X = M (ω2 X − A) = −M A (ω02 + 2 i ζ ω0 ω) ⁄ (ω02 − ω2 + 2 i ζ ω0 ω).
Influencia del tamaño del pecho
Vamos a introducir otra simplificación enorme: asumimos que podemos colapsar la geometría del pecho en un único parámetro relevante: una longitud l que representa el tamaño. Para fijar ideas, tomamos que las constantes del oscilador armónico amortiguado están relacionadas con el tamaño de la siguiente manera (que sale de asumir un modo de cortadura pura con amortiguamiento proporcional a la rigidez):
- M ≡ M0 l3;
- F ≡ F0 l;
- K ≡ K0 l.
La frecuencia natural y el factor de amortiguamiento se derivan de las constantes anteriores:
- ω0 = √(K0 ⁄ M0) ⁄ l;
- ζ = F0 ⁄ [2 √(K0 M0) l].
Ahora queda introducir estas expresiones en la fuerza de reacción. Esta fuerza es directamente proporcional a la aceleración de entrada, así que podemos calcular la respuesta con aceleración unidad y escalarla para cualquier aceleración dada. Además de esto, el análisis dimensional nos dice que podemos redefinir las unidades de medida y asignar el valor 1 a 3 constantes diferentes; nos libraremos de la pulsación de los saltos ω, la constante de la inercia M0 y la constante de la rigidez K0. Con esta redefinición, la fuerza de reacción queda así:
|R| = √{[(1+F02) l6] ⁄ [l4 − 2 l2 + (1+F02)]};
arg(R) = atan{[F0 l2] ⁄ [l2 − (1+F02)]}.
La constante del amortiguamiento, que es algo que habría que medir para ajustar el modelo a la realidad dentro de cierto rango de tamaños de pecho, influye en el comportamiento cualitativo de la fuerza de reacción, que tiene un máximo local cuando el amortiguamiento es bajo. Este máximo local indica la presencia de un efecto de resonancia: un pecho de cierto tamaño concreto tiene una frecuencia de resonancia que más o menos coincide con la frecuencia de los rebotes de la carrera o de los saltos, así que las molestias son máximas localmente y se reducirían con un pecho ligeramente más pequeño o ligeramente más grande. Veremos que esta resonancia es más una curiosidad matemática que un problema real.
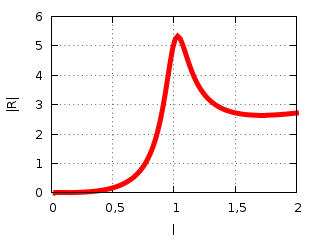
Magnitud de la fuerza de reacción en función del tamaño del pecho
para un amortiguamiento bajo que bien podría no tener nada que ver con
el real. El máximo local se da con un tamaño de pecho tal que su
frecuencia de resonancia más o menos coincide con la de los rebotes de
la carrera o de los saltos. Este máximo local es difícil de alcanzar
en la práctica.
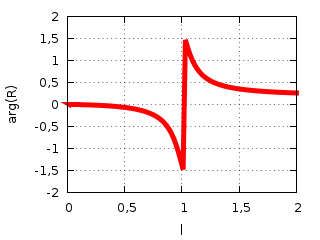
Desfase de la fuerza de reacción en función del tamaño del pecho
para un amortiguamiento bajo que bien podría no tener nada que ver con
el real. La singularidad no es más que un efecto del valor principal
usado para el argumento (por haberlo elegido
entre −π
y π) y se da con un tamaño de pecho tal
que su frecuencia de resonancia más o menos coincide con la de los
rebotes de la carrera o de los saltos: un pecho más pequeño reacciona
con retardo frente a la excitación, mientras que uno más grande se
adelanta (o se retrasa tanto que queda más cerca de estar adelantado
al movimiento periódico). Esta resonancia es difícil de alcanzar en
la práctica.
Salvo por el fenómeno de la resonancia, la tendencia general es a aumentar la fuerza de reacción (y, con ello, las molestias) con el tamaño del pecho. La solución, por supuesto, consiste en usar un sujetador deportivo, que aumenta la rigidez (y, con ello, la frecuencia de resonancia), lo que reduce la reacción, que además se reparte de una manera más benigna.
La resonancia no es fácil de alcanzar en la práctica
Dentro del régimen razonablemente elástico, el busto de una mujer tiene una frecuencia natural en el entorno de algunos Hz (una pulsación natural ω0 de algunas decenas de rad s−1). En general, podemos asumir que la frecuencia de los rebotes al correr o al saltar es más baja y no se llega al punto de resonancia. Los armónicos de orden superior pueden notarse, pero su amplitud es pequeña. Un pecho muy grande puede tener su frecuencia de resonancia próxima a la de los pasos, pero antes se producen fenómenos no lineales importantes que anulan la validez cuantitativa de este análisis (aunque no el hecho de que la actividad física vigorosa sin una buena sujeción puede causar dolor).
En los casos más comunes, no se alcanza la resonancia y, por lo general, un busto voluminoso sufre más molestias que uno pequeño. Los sujetadores deportivos sirven para paliar este problema.
Categorías: Física
Disolver sal común en agua es un proceso endotérmico
2015-01-10
La disolución de sal común en agua es endotérmica. Un poco de agua, un poco de sal, una balanza y un termómetro son el material necesario para un experimento químico muy sencillo que puede hacerse en casa y que divertirá a los estudiantes curiosos que empiezan a tratar estos conceptos.
Modelo del comportamiento térmico de la disolución de sal común en agua
Disolver sal común en agua es un proceso que no es energéticamente neutro. Hace falta aportar energía para romper la red cristalina de la sal y los enlaces de hidrógeno entre las moléculas de agua, mientras que la formación de enlaces entre el agua y los iones de cloro y sodio libera energía. A temperatura ambiente, el resultado es tal que el proceso completo absorbe cierta energía: la entalpía de disolución de la sal común en agua es ΔH ≈ 3,9 kJ mol−1.
La entalpía de disolución sale de alguna parte: de la energía térmica de la propia disolución. En primera aproximación, como hay mucha más masa de agua que de sal, podemos asumir que todo el cambio de energía térmica sale de la masa mH2O de agua, que se comporta como un fluido caloríficamente perfecto con una capacidad térmica específica c = 4,2 kJ kg−1 K−1.
La última propiedad importante del cloruro sódico que necesitamos es su masa molar: M ≈ 58 g mol−1.
Al disolver una masa mNaCl de sal común en una masa mH2O ≫ mNaCl de agua, se absorbe una entalpía
mNaCl ΔH ⁄M.
Esto provocará un descenso de temperatura ΔT de la disolución. Como casi todo es agua, el cambio de energía térmica se debe más que nada al disolvente. Este descenso de energía térmica es
mH2O c ΔT.
La entalpía de disolución es igual al cambio de energía térmica:
mNaCl ΔH ⁄M = mH2O c ΔT.
Ahora es posible introducir los valores de las constantes que vimos arriba para despejar una relación entre la masa de agua mH2O, la masa de sal mNaCl y el descenso de temperatura ΔT. Por ejemplo, podemos ver que hace falta añadir una masa mNaCl entre 12 g y 13 g para enfriar ΔT ≈ 1 K una masa mH2O ≈ 200 g de agua.
Confirmación experimental de la validez del modelo
Podemos verificar con un experimento doméstico que el modelo representa razonablemente bien la realidad. Las siguientes imágenes ilustran el proceso:

Pesando el agua. En este
caso, mH2O = 200 g.

Pesando la sal común. En este
caso, mNaCl = 12,6 g.

Temperatura del agua antes de añadir la sal. El termómetro marca
13,3 °C.

Añadiendo la sal. Hizo falta remover bien para disolverla
adecuadamente.

La temperatura final de la disolución es
de 12,4 °C, con lo que el descenso de
la temperatura es ΔT =
0,9 K, casi lo predicho. La temperatura aumentaba
lentamente para equilibrarse con el ambiente. Al repetir el
experimento varias veces y remover con más premura, el descenso de
temperatura igualó el valor predicho
de 1,0 K.
Las masas de agua y sal y el descenso de temperatura se relacionan mediante la ley
ΔT mH2O ⁄ mNaCl = ΔH ⁄ (M c) = A,
donde A es una constante que es fácil de determinar a partir de un experimento similar al anterior. Puede ser instructivo realizar dicho experimento con diferentes cantidades de agua y sal para determinar el valor de la constante.
Categorías: Química
Permalink: https://sgcg.es/articulos/2015/01/10/disolver-sal-comun-en-agua-es-un-proceso-endotermico/
Breve apunte sobre la prevaricación y la corrupción
2015-01-09
Me dio por leer unos comentarios a una noticia sobre un escándalo político reciente. Una de las personas en las que se centraba la noticia recibía acusaciones de corrupción y de prevaricación. Un comentarista matenía con vehemencia que la prevaricación es necesariamente corrupción. A pesar de que tanto la prevaricación como la corrupción pueden ser actos muy feos y dañinos, son en realidad conceptos ortogonales que a menudo se superponen:
- un servidor público comete prevaricación cuando dicta a sabiendas una resolución injusta;
- un servidor público comete un acto de corrupción cuando abusa del poder que le da su especial condición para obtener un beneficio ilegítimo (no necesariamente económico, aunque habitualmente lo es).
La prevaricación puede ser una suerte de herramienta para un corrupto, pero no es estrictamente necesaria: hay más actos de corrupción y no todos los actos de prevaricación concebibles proporcionan (o buscan proporcionar) el beneficio ilegítimo que exige la corrupción, salvo quizá para definiciones muy amplias e inclusivas del concepto de «beneficio». Podemos imaginar, por ejemplo, el caso de un juez que dicta a sabiendas una sentencia incompatible con la ley no con el fin de obtener un beneficio ilegítimo, sino por motivos religiosos: cree que sigue la voluntad de los dioses. En la práctica, no obstante, la prevaricación como acto específico de corrupción es tristemente fácil de encontrar.
Categorías: Lingüística
Permalink: https://sgcg.es/articulos/2015/01/09/breve-apunte-sobre-la-prevaricacion-y-la-corrupcion/
