Teoría de juegos en el parque acuático
2009-08-23
Doy gracias a G.A. por sugerir el tema de este artículo.
El otro día estuve en un parque acuático con unos amigos. Este parque tiene unas atracciones que requieren el uso de unos enormes flotadores sobre los que uno se monta para descender a gran velocidad por deslizaderos de diversas formas. Hay unos pocos flotadores disponibles para su uso sin coste adicional, pero su número es muy limitado. De lo que sí está bien provisto el parque es de flotadores de alquiler que hay que pagar aparte del precio de la entrada y que se diferencian de los disponibles sin coste adicional simplemente por su color y por el celo de quienes los llevan. Dado que casi todos los visites forman pequeños grupos de tamaños diversos y los flotadores «gratuitos» (que no lo son, ya que vienen incluidos en el precio de la entrada) son escasos, existe cierto beneficio aparente en usar flotadores de alquiler cuando no hay mucha gente con ellos. Según aumenta el uso de los flotadores de alquiler, los usuarios de los flotadores «gratuitos» notan un perjuicio: en efecto, la espera aumenta para ellos porque los flotadores «gratuitos» han de hacer recorridos completos en las colas para que sus usuarios avancen puestos, mientras que quienes disfrutan de los flotadores de alquiler pueden progresar de forma convencional. El atractivo directo de los flotadores de alquiler se reduce conforme aumenta su uso, pues el tiempo de espera se hace mayor pero el precio del alquiler no cambia. Los flotadores de alquiler se vuelven atractivos de forma indirecta por comparación con los flotadores «gratuitos». Sea cual sea el motivo, lo cierto es que los flotadores de alquiler son extremadamente populares y casi todo el público parece llevar uno.
Este fenómeno se da en mayor o menor medida en todos los parques de ocio en los que existe la figura del cliente premium que, a cambio de un desembolso adicional al común, obtiene la promesa de unos tiempos de espera reducidos. Si el coste adicional para ascender a la categoría premium es lo bastante pequeño, entonces es de esperar que la mayoría del público acabe en esta opción, anulando cualquier posible beneficio. Cuando la proporción de clientes premium es baja, entonces éstos se ven beneficiados sin afectar en gran medida a los clientes convencionales. En algún punto intermedio está el máximo perjuicio para el cliente convencional con un beneficio moderado para el cliente de pago.
Podemos modelar el problema del cliente premium como un juego de N jugadores. Sean Nc el número de clientes convencionales, Np el número de clientes premium (Nc + Np = N), Tc el tiempo de espera de los clientes convencionales, Tp el tiempo de espera de los clientes premium y Fc el número de puestos de clientes convencionales en una cola, de modo que el modelo es aplicable al caso del parque acuático. Suponiendo que los clientes van de uno en uno en las colas, el tiempo de espera de los clientes premium será, en unidades escogidas astutamente, Tp = Np + min(Fc, Nc) (los clientes premium tienen preferencia), mientras que el tiempo de espera de los clientes convencionales será Tc = Nc (Np + min(Fc, Nc)) ⁄ min(Fc, Nc) (los clientes convencionales han de esperar a que sus puestos estén disponibles). El tiempo de espera de los clientes premium crece linealmente con su proporción hasta un quiebro y a partir de allí se mantiene constante y no existe beneficio. El tiempo de espera de los clientes convencionales aumenta fuertemente con el número de clientes y alcanza un máximo cuando el número de clientes premium es Np = (N − Fc) ⁄ 2, siendo entonces Tc = (N + Fc)2 ⁄ (4Fc) y Tp = (N + Fc) ⁄ 2. Cuando el número de clientes premium es muy grande, de modo que el número de clientes convencionales es igual o menor que el número de puestos para clientes convencionales, los tiempos de espera de ambos tipos de cliente se igualan y no existe ventaja para los clientes premium.
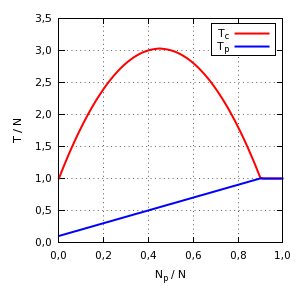
Tiempos de espera para
Fc = 0,1N.
Modelar el beneficio o coste percibido por cada tipo de cliente es algo más difícil. Podemos partir de un beneficio base correspondiente a una clientela compuesta exclusivamente de clientes convencionales y suponer que los pagos extra son proporcionales a la diferencia de tiempos de espera. El incremento en la utilidad percibida por los clientes convencionales será, en unidades de tiempo de espera, Uc = Tp − Tc, mientras que el incremento correspondiente a los clientes premium será Up = Tc − Tp − Cp, donde Cp es el coste adicional que han de pagar los clientes premium.
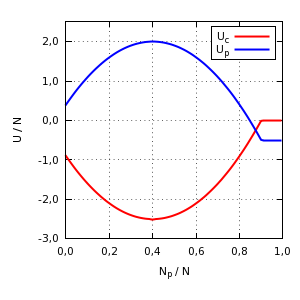
Incrementos en las utilidades percibidas para un número de puestos
para Fc = 0,1N y
Cp = 0,5N.
Los pagos correspondientes a elegir ser cliente convencional o premium serán estos incrementos de utilidad si suponemos que la elección es definitiva y se realiza al comenzar la jornada. Salvo cuando el sobrecoste premium Cp es muy alto, parece conveniente ser cliente premium. ¡Vemos que si todos los clientes escogen esta estrategia, entonces salen perdiendo! En la práctica, por supuesto, la percepción de la utilidad es más complicada e incluso inconsistente y variable en el tiempo. Ahora bien, si suponemos que el modelo es válido y añadimos la posibilidad de que los clientes se pasen a la opción premium con el tiempo, entonces lo harán, si están bien informados y son racionales, hasta que las utilidades de las dos opciones se igualen, es decir, hasta que Np = (N − 2 Fc + (N2 + 2 Cp Fc)1⁄2) ⁄ 2. La utilidad es negativa en este punto. Para valores del sobrecoste premium superiores a Cp = 2(Fc − N), existe otro punto de corte de las curvas de utilidad en Np = (N − 2 Fc − (N2 + 2 Cp Fc)1⁄2) ⁄ 2 y no habrá clientes premium. En cada instante, los clientes convencionales juegan a ascender a la categoría premium o quedarse como están. El pago por ascender será la diferencia de la utilidad premium en el siguiente instante y la utilidad convencional en el instante actual. Los clientes premium ya existentes, en cambio, no cambian de categoría. Si es (Np)i el número de clientes premium en el instante actual y (Np)i+1 el número de clientes premium tras la toma de decisión, a un cliente convencional le resulta conveniente cambiar de categoría sin importar el resultado del juego, (Np)i+1, siempre que su utilidad actual sea menor que la mínima que puede obtener el cliente premium, −Cp, es decir, siempre que (Np)i < (N − 2Fc + (N2 − 4Cp Fc)1⁄2) ⁄ 2. Además de esto, nunca conviene cambiar de categoría más allá del punto de corte de las curvas de utilidad.
Para terminar, vamos a ver cómo progresaría el número de clientes premium a lo largo de la mañana. Supongamos un modelo dinámico sencillo tal que la variación temporal del número de clientes premium va con el salto de utilidades: dNp ⁄ dt = Up − Uc. Las unidades de tiempo son arbitrarias. Los puntos de equilibrio son los indicados en el párrafo anterior. El primero de los puntos de equilibrio, el de mayor valor de Np, es estable, mientras que el segundo, que sólo existe cuando el valor de Cp es grande, es inestable. El modelo es válido entre el origen o el punto de equilibrio inestable (si éste es mayor que 0) y el punto de equilibrio estable, pues es entonces cuando el número de clientes premium aumenta. Veamos cómo crece muy rápidamente el número de clientes premium para los valores de los parámetros que hemos manejado hasta ahora:
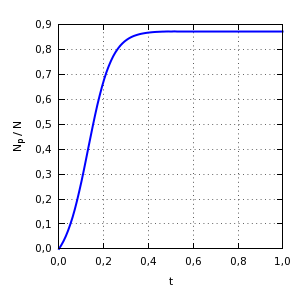
Evolución en el tiempo del número de clientes premium para
Fc = 0,1N y
Cp = 0,5N a partir
de la condición inicial
Np = 0.
¡Vemos que, con este modelo, el número de clientes premium va a crecer de forma espontánea hasta un valor bastante grande y muy próximo a N − Fc! Para estos parámetros, los clientes premium son mayoría (Np = 0,874N) y esperan colas largas (Tp = 0,974N) y los clientes convencionales superan ligeramente el número de plazas disponibles para ellos (Nc = 0,126N = 1,26Fc) y se ven un poco perjudicados (Tc = 1,22N). Por supuesto, el público se comporta de una manera más sofisticada que la que describe este modelo, pero nos hemos hecho una idea aproximada de la mecánica que hace que haya tal proporción de clientes premium (¡con grandes flotadores de alquiler!) en algunos parques de ocio y hemos visto que la situación no es muy beneficiosa para los clientes.
Categorías: Matemáticas
Permalink: https://sgcg.es/articulos/2009/08/23/teoria-de-juegos-en-el-parque-acuatico/
