Ley de los gases ideales
2010-04-08
La ley de los gases ideales es un modelo matemático extremadamente sencillo y útil que sirve para predecir el comportamiento de gases en equilibrio a presiones no muy elevadas. Relaciona la presión, la temperatura y la cantidad de gas presente por unidad de volumen. Las aplicaciones de la ley de los gases ideales son muy amplias y tan dispares como la meteorología, la aerodinámica y la anestesiología. Si la ley de los gases ideales se queda corta, hay modelos más complicados con rangos de validez más amplios.
Podemos deducir la ley de los gases ideales mediante un sencillo experimento mental. Supongamos que tenemos un gas metido en una cajita aislada del mundo exterior. Modelaremos las partículas del gas como pequeñas bolitas elásticas que están colisionando en todo momento contra las paredes de la caja. Miremos de cerca una de las paredes. Las partículas se acercan a la pared, chocan contra ella, rebotan y se alejan de la pared, de modo que cambian la dirección de su cantidad de movimiento.
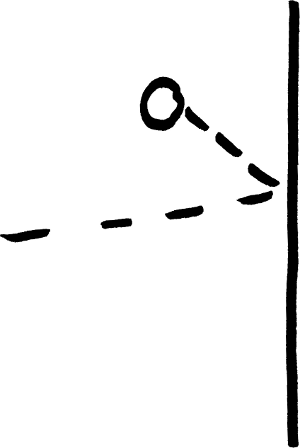
Las partículas rebotan contra las paredes.
Como la cantidad de movimiento del sistema completo ha de mantenerse constante, la pared recibe una cantidad de movimiento que compensa la variación del ímpetu de la partícula que rebota y que en media es proporcional a la celeridad media de las partículas. Dejemos pasar un poco de tiempo. Contra la pared habrán chocado un número de partículas que es evidentemente proporcional al número total de partículas que hay dentro de la caja.
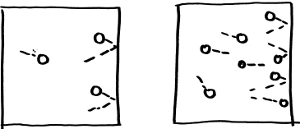
Las colisiones son más frecuentes conforme aumenta el número
de partículas.
El número de colisiones también es proporcional a la rapidez media de las partículas y al tiempo transcurrido.
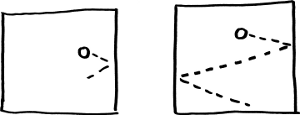
Las partículas tienen más tiempo para chocar contra las paredes
cuando se mueven deprisa y cuando el tiempo transcurrido es largo.
Por último, el número de colisiones es inversamente proporcional a la distancia de pared a pared.
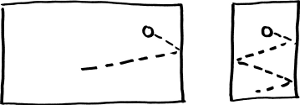
Las partículas tienen más tiempo para chocar contra las paredes
cuando el camino a recorrer es corto.
Cada uno de estos choques aporta un ímpetu a la pared que es en media proporcional a la rapidez media de las partículas, de modo que el ímpetu total que absorbe la pared en un tiempo dado es proporcional al cuadrado de la celeridad media de las partículas, al número de partículas que hay en la caja y al tiempo transcurrido y es inversamente proporcional al tamaño de la caja. La fuerza es la variación de la cantidad de movimiento con el tiempo, así que el ímpetu recibdo por la pared dividido entre el tiempo transcurrido da como resultado la fuerza a la que está sometida la pared. La presión es la fuerza aplicada por unidad de superficie, así que la fuerza a la que está sometida la pared dividida por la superficie de la pared da como resultado la presión a la que está sometida la pared. Esta presión es, por lo tanto, proporcional al cuadrado de la rapidez de las partículas e inversamente proporcional a la distancia de pared a pared y la superficie de la pared. El volumen de la caja crece con el producto de la superficie de la pared y la distancia entre paredes. La energía cinética de las partículas va con el cuadrado de su rapidez, pero lo habitual no es medir la energía cinética, sino una cantidad proporcional a ésta, la temperatura.
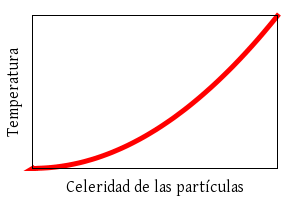
La temperatura y la energía cinética son proporcionales. La
energía cinética es proporcional al cuadrado de la rapidez media de las
partículas.
Si juntamos todo, vemos que la presión es directamente proporcional a
la temperatura y al número de partículas e inversamente proporcional
al volumen de la caja. La forma habitual de escribir esta relación
es la siguiente:
p V = n R T
donde:
- p ≡ presión;
- V ≡ volumen;
- n ≡ cantidad de materia del gas;
- R ≅ 8,314 J mol−1 K−1;
- T ≡ temperatura.
La anterior relación es la ley de los gases ideales.
La ley de los gases ideales combina las leyes empíricas de
Boyle-Mariotte:
p ∝ V−1
(a temperatura constante),
Charles:
V ∝ T
(a presión constante)
y Gay-Lussac:
p ∝ T
(a volumen constante).
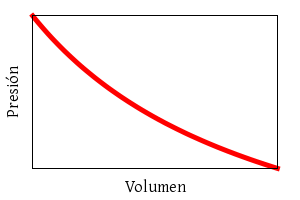
Ley de Boyle-Mariotte.
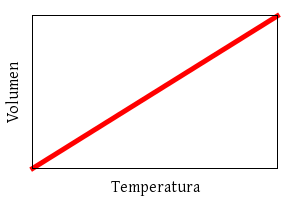
Ley de Charles.
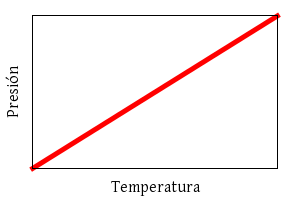
Ley de Gay-Lussac.
Permalink: https://sgcg.es/articulos/2010/04/08/ley-de-los-gases-ideales/
