Ondas planas y relaciones de dispersión
2011-09-25
Hace mucho tiempo desde la última vez que escribí un artículo sobre física y matemáticas. ¡Esto no puede seguir así!
Las ondas son fenómenos de propagación en el espacio y en el tiempo. Podemos usar el concepto de onda para describir numerosísimos fenómenos: las olas del mar, los rayos de luz, los sonidos, las moléculas de aire dentro de una cajita… todas estas cosas son ondas a efectos prácticos.
Hay muchos tipos de onda. En este artículo vamos a estudiar las ondas planas, que son ondas que avanzan en el espacio de modo que los frentes de onda son planos perpendiculares a la dirección de propagación. Para concretar, vamos a trabajar en este artículo con ondas planas sinusoidales. Es decir, si paramos el tiempo, notamos lo siguiente:
- la onda sube y baja sinusoidalmente si avanzamos en la dirección de propagación;
- la onda no cambia de valor si avanzamos en un plano perpendicular a la dirección de propagación.
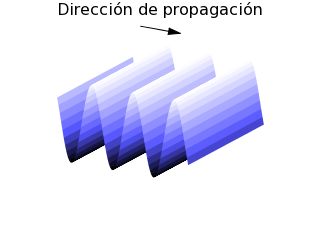
Onda plana sinusoidal en un espacio bidimensional.
Vamos a introducir unos pocos símbolos matemáticos.
Usaremos el símbolo t
para hablar de la coordenada temporal, el símbolo
x para
hablar de las coordenadas espaciales, el símbolo A(t,x) para hablar
de la amplitud de la onda en función del tiempo y del espacio, ω para hablar de la pulsación angular
de la onda (lo rápido que pasa de subir a bajar y de bajar a subir)
y el símbolo k para hablar
del número de onda (un vector tan largo como la longitud de onda y
que apunta en la dirección de propagación). Con estos símbolos,
la amplitud A(t,x)
de la onda plana adopta esta forma tan sencilla:
A(t,x) = Ak ei(k⋅x−ωt).
La constante Ak es en
general compleja y, por lo tanto, contiene información tanto de
la amplitud como de la fase inicial de la onda. ¡Un momento!
El valor de esta onda es un número complejo. ¿Hay algún
problema en esto? ¡Por supuesto que no! Si la onda que estamos
midiendo sólo tiene un valor real, entonces tomamos la parte real
de la anterior expresión y asunto resuelto. Por cierto, tanto
A(t,x) como Ak pueden ser
escalares, vectores, tensores, espinores o cualquier otro tipo de
objeto matemático que sirva para nuestro modelo físico. Si
superponemos ondas planas en diferentes direcciones y con diferentes
parámetros, podemos reconstruir ondas de formas complicadas.
Esta expresión de la onda plana está muy bien, pero tenemos que relacionarla de alguna manera con el fenómeno físico que estamos modelando. ¡Hay muchos fenómenos que no admiten ondas planas como soluciones! ¿Cuáles sí lo hacen? En general, fenómenos de campos lineales y no estacionarios que suceden en un espacio y un tiempo infinitos. Las ondas planas son buenos modelos para la propagación de la luz en el vacío, por ejemplo, o para las olas en la superficie de un océano inmenso. Todos estos fenómenos están modelados mediante ecuaciones de campo, que pueden ser de muy diversos tipos: diferenciales, integrales, variacionales… Lo que tenemos que hacer es introducir la solución de onda plana en las ecuaciones de campo y ver qué propiedades han de cumplir la amplitud Ak, la pulsación ω y el número de onda k para verificar las ecuaciones. Estas relaciones serán unas relaciones de compatibilidad (por ejemplo, las que dictan que el campo magnético y el campo eléctrico son perpendiculares en un rayo de luz) y unas relaciones de dispersión que indican cómo están relacionados el número de onda y la pulsación.
Ejemplo: ecuación de ondas unidimensional
La ecuación de ondas unidimensional es muy famosa y muy fácil de
resolver. Es el prototipo de ecuación hiperbólica de segundo orden.
Sus soluciones se propagan en el espacio hacia adelante y hacia atrás
sin pérdidas. Esta ecuación sirve para modelar fenómenos tan
aparentemente dispares como el sonido en un pasillo largo y estrecho,
un rayo de luz y el campo de velocidades alrededor de un obstáculo
bidimensional y muy delgado en una corriente de aire supersónica
(en este caso, la dirección de la corriente actúa a modo de «tiempo»
y la dirección perpendicular al obstáculo actúa a modo de «espacio»).
Para un campo u(t,x),
la ecuación de ondas es ésta:
∂2u ⁄ ∂t2 + c2 ∂2u ⁄ ∂x2 = 0.
La constante c es la rapidez a la
que se propagan las ondas.
Introduzcamos la solución de onda plana
u(t,x) = uk ei(kx−ωt)
en la ecuación de ondas. Tras operar un poco, obtenemos
la siguiente relación de dispersión:
ω2 − c2 k2 = 0.
Según esto, la pulsación ω
y el número de onda k son directamente
proporcionales.
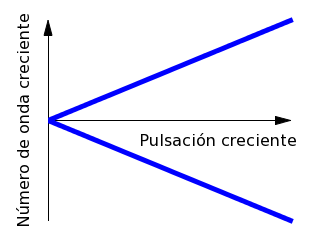
Relación de dispersión de la ecuación de ondas unidimensional.
Ejemplo: ecuación de Schrödinger de la partícula libre
La ecuación de Schrödinger sirve para modelar el comportamiento de
pequeñas partículas no relativistas y olas de pequeña amplitud en la
superficie del agua (aunque la ecuación de Schrödinger para las olas
del agua en el régimen interesante tiene un término no lineal). Con
las unidades adecuadas, la ecuación de Schrödinger para un campo libre
u(t,x) es ésta:
i ∂u ⁄ ∂t = −∇2 u.
El operador ∇2 es
la laplaciana, la suma de las derivadas segundas en todas las direcciones
del espacio.
Introduzcamos la solución de onda plana
u(t,x) = uk ei(k⋅x−ωt)
en la ecuación de campo. Tras unas sencillas operaciones, obtenemos
la siguiente relación de dispersión:
ω = k ⋅ k.
En este caso, la relación entre la pulsación y el número de onda es no lineal. Se dice que la ecuación de campo es dispersiva, ya que ondas de distinta frecuencia se propagan a velocidades distintas.
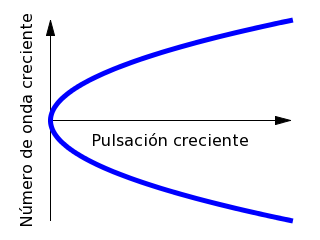
Relación de dispersión de la ecuación de Schrödinger libre.
Ejemplo: acústica
Para terminar, vamos a ver cómo se comportan dos campos acoplados,
el de presión y el de velocidades, como pequeñas perturbaciones en
un gas ideal estacionario. El campo de perturbaciones de presión
es p(t,k)
y el campo de velocidades de perturbación es u(t,x).
Es llegar a las ecuaciones de campo que, en las unidades adecuadas
(en concreto, la presión está expresada en unidades de la presión
de la atmósfera en calma dividida por la densidad de la atmósfera
en calma), son así de bonitas:
a−2 ∂p ⁄ ∂t + ∇ ⋅ u = 0;
∂u ⁄ ∂t + ∇p = 0.
La constante a es la rapidez del
sonido.
Introduzcamos la solución de onda plana
p(t,x) = pk ei(k⋅x−ωt);
u(t,x) = uk ei(k⋅x−ωt)
en las ecuaciones de campo. Tras unas pocas manipulaciones, obtenemos
lo que sigue:
−a−2 ω pk + k ⋅ uk = 0;
−ω uk + k pk = 0.
Tras manipular un poco, nos queda este par de relación de
compatibilidad y relación de dispersión:
uk = (k ⁄ k) (pk ⁄ a);
ω = a k.
En las ecuaciones anteriores, k
es el módulo del vector de número de onda k. La relación de dispersión
es como la que obtuvimos para la ecuación de ondas unidimensional.
Para una pulsación dada, todos los números de onda que cumplen
la relación de dispersión forman una esfera. La relación de
compatibilidad dice que las velocidades de perturbación van en la
dirección de propagación de la onda acústica y que su magnitud es
proporcional a la de la perturbación de presión.
Categorías: Física, Matemáticas
Permalink: https://sgcg.es/articulos/2011/09/25/ondas-planas-y-relaciones-de-dispersion/
