Derivada convectiva
2011-10-04
Sigue avanzando esta suerte de cursillo acelerado de conceptos de mecánica de medios continuos para lectores incautos que no le hacen ascos a un poquito de matemáticas.
La derivada convectiva es una generalización de la derivación con respecto del tiempo que se usa mucho en mecánica de medios continuos (como la mecánica de fluidos). Ayer vimos la diferencia entre las descripciones lagrangiana y euleriana. La derivada convectiva relaciona el ritmo de variación con el tiempo de una propiedad de una partícula material (es decir, en la descripción lagrangiana) con el ritmo de variación temporal de la propiedad instantánea en un punto fijo del espacio (es decir, en la descripción euleriana).
La derivada sustancial o convectiva, con la notación que
introduciremos más adelante, tiene este aspecto tan vistoso:
D ⁄ Dt = ∂ ⁄ ∂t + v ⋅ ∇.
No es más que una de las muchas generalizaciones del concepto de
derivada que aparecen a menudo en problemas de la física matemática.
La derivada temporal en la descripción lagrangiana y en la descripción euleriana
Fijemos nuestra atención en una partícula material, es decir, adoptemos una descripción lagrangiana. La partícula material está identificada por su posición de partida X0. La partícula material tiene una propiedad Cl(t,X0). Para fijar ideas, podemos suponer que esta propiedad es la temperatura de una partícula de aire. Esta propiedad varía al transcurrir el tiempo con un ritmo (d ⁄ dt)Cl(t,X0).
Ahora fijemos nuestra atención en un punto fijo del espacio, es decir, adoptemos una descripción euleriana. Este punto está identificado mediante el símbolo x. En cada instante, nuestro punto del espacio está ocupado por una partícula material, pero las partículas materiales pueden moverse, así que la que ocupa el punto fijo del espacio puede variar con el tiempo. Podemos asignarle una propiedad Ce(t,x) a nuestro punto fijo; esta propiedad es la de la partícula material que lo ocupa en cada instante. Para fijar ideas, podemos suponer que esta propiedad es la temperatura medida por un termómetro fijo metido dentro de una corriente de aire. El ritmo de variación temporal de la propiedad del punto es (∂ ⁄ ∂t)Ce(t,x).
Hemos definido la derivada temporal de la partícula material (la de la descripción lagrangiana) y la derivada temporal del punto fijo en el espacio (la de la descripción euleriana). En un momento dado, la partícula material X0 puede ocupar el punto del espacio x. En ese momento, la propiedad del punto, Ce(t,x) es la de la partícula que lo ocupa, Cl(t,X0). Las derivadas temporales, en cambio, no tienen por qué ser iguales. Esto no es sólo obvio matemáticamente (tenemos dos funciones distintas que sólo coinciden en un instante dado); podemos comprobar esto con un sencillo experimento mental con el ejemplo del aire y el termómetro fijo. En efecto, supongamos que justo tras la partícula de aire que estamos estudiando viene otra mucho más caliente; en tal caso, la medida del termómetro subirá muy deprisa, pero la partícula de aire original se calienta muy despacio, ya que tiene muy mala conductividad térmica.
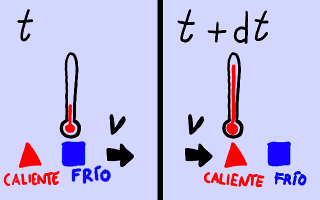
En el instante t, la partícula
fría se encuentra a la altura del termómetro fijo. En el instante
t + dt, la partícula
caliente ha pasado a ocupar su lugar. El termómetro se ha calentado
muy deprisa, pero cada partícula conserva su temperatura.
Relación entre las dos derivadas: la derivada convectiva
Las partículas materiales se mueven. En cada punto x podemos medir la velocidad instantánea de la partícula que lo ocupa y definir, con ello, un campo de velocidades v(t,x). Los puntos del espacio están fijos; el campo de velocidades es la velocidad a la que las particulas materiales atraviesan cada punto.
Fijémonos en un punto fijo del espacio, x. En el instante t, sus propiedades son Ce(t,x).
Tras un cortísimo espacio de tiempo dt,
sus propiedades habrán pasado a valer
Ce(t+dt,x) = Ce(t,x) + (∂ ⁄ ∂t)Ce(t,x) dt.
De igual manera, si mantenemos fijo el tiempo y pasamos a medir
a un punto próximo x + dx
(separado por una distancia infinitesimal), las propiedades pasan a valer
Ce(t,x+dx) = C(t,x) + ∇C(t,x) ⋅ dx.
Fijémonos en la partícula material X0. En el instante t, ocupa la posición del espacio x y se mueve con velocidad v(t,x).
Tras un cortísimo espacio de tiempo, en el instante t + dt,
pasa a la posición x + v(t,x) dt,
es decir, experimenta un desplazamiento infinitesimal
dx = v(t,x) dt.
Sus propiedades pasan del valor
Cl(t,X0) = Ce(t+dt,x+dx).
Con lo que sabemos del párrafo
anterior, deducimos que el incremento dCl(t,x)
de las propiedades entre ambos instantes es
dCl(t,x) = (∂ ⁄ ∂t)Ce(t,x) dt + ∇Ce(t,x) ⋅ v(t,x) dt.
Si dividimos entre el incremento infinitesimal de tiempo dt, obtenemos la relación entre la derivada
temporal de la partícula material y las derivadas parciales temporal
y espacial de la descripción euleriana:
(d ⁄ dt)Cl = (∂ ⁄ ∂t)Ce + v ⋅∇Ce ≡ (D ⁄ Dt)Ce.
Hemos introducido el símbolo
D ⁄ Dt ≡ (∂ ⁄ ∂t) + v ⋅ ∇
para referirnos a la derivada convectiva o derivada
sustancial. Este nombre viene se debe al término dependiente de
la velocidad, el término convectivo, que es el que describe
los cambios de las propiedades en un punto debido al desplazamiento
de las partículas materiales, es decir, la convección. Hay
autores que usan otros nombres.
Fuente de no linealidades
La derivada temporal habitual es un operador lineal con todas sus útiles propiedades: la derivada de una suma es la suma de las derivadas, la derivada de una función multiplicada por una constante es igual a la constante multiplicada por la derivada de la función… Si el campo sometido a la derivada convectiva no tiene términos en la velocidad, entonces la operación también es lineal, aunque probablemente no es invariante frente a traslaciones. Si el campo sometido a la derivada convectiva tiene términos en la velocidad (por ejemplo, si estamos usando las leyes de Newton que relacionan el ritmo de variación temporal de la velocidad con las fuerzas aplicadas), en cambio, la derivada convectiva pasa a ser un operador no lineal, fuente de complejidad y quebraderos de cabeza para quien quiere resolver las ecuaciones. Esta no linealidad, por supuesto, sólo es una manifestación de la misma no linealidad que aparecería en otra parte, probablemente de forma implícita, en las ecuaciones planteadas con una descripción lagrangiana (por ejemplo, los esfuerzos viscosos, que en un fluido newtoniano dependen linealmente del gradiente de velocidad, tienen una expresión complicada y dependiente de la historia del fluido en la descripción lagrangiana). En las no linealidades está, no obstante, la chispa que hace que el universo se comporte de forma tan interesante.
Categorías: Física, Matemáticas
Permalink: https://sgcg.es/articulos/2011/10/04/derivada-convectiva/
