Ecuaciones de Euler de la mecánica de fluidos (1)
2011-10-22
∫∫∫V (∂⁄∂t) ρ dV + ∫∫S ρ v ⋅ n dS = 0
∫∫∫V (∂⁄∂t) (ρv) dV + ∫∫S (ρv⊗v+pI) ⋅ n dS = 0
∫∫∫V (∂⁄∂t) (ρe+ρv2⁄2) dV + ∫∫S (ρe+ρv2⁄2+p) v ⋅ n dS = 0.
Las anteriores ecuaciones son, interpretados los símbolos de forma adecuada, una de las formas (la forma integral de conservación) adoptadas por las ecuaciones de Euler de la dinámica del fluido no viscoso son un modelo matemático extraordinariamente útil y bello que tiene grandes aplicaciones en campos como el diseño aerodinámico. Sirven para modelar un fluido:
- sin viscosidad;
- sin conductividad térmica;
- sin campos de fuerza (sin efectos gravitatorios, por ejemplo);
- sin reacciones químicas;
- sin transferencia de calor por radiación;
- sin efectos relativistas (mucho más lento que la luz);
- modelable como un medio continuo (así que no valen para atmósferas muy enrarecidas).
Estas hipótesis, aunque parecen restrictivas, son aplicables a muchísimos casos de interés práctico. El aire alrededor de un vehículo con buenas formas aerodinámicas (por ejemplo, un avión) a velocidades no demasiado elevadas, por ejemplo, responde muy bien a las ecuaciones de Euler salvo en regiones muy pequeñas (las capas límite, las estelas y los chorros).
Las ecuaciones de Euler son unas ecuaciones de conservación:
- de conservación de la masa;
- de conservación de la cantidad de movimiento;
- de conservación de la energía.
Vamos a ver cómo deducir su forma. Antes, introduzcamos cierta notación:
- t es el tiempo;
- ρ es la densidad del fluido (depende del tiempo y del punto del espacio);
- v es la velocidad a la que se mueve el fluido (depende del tiempo y del punto del espacio);
- p es la presión (depende del tiempo y del punto del espacio);
- e es la energía interna del fluido por unidad de masa (depende del tiempo y del punto del espacio), es decir, su energía total menos su energía cinética.
Ecuación de conservación de la masa
Centrémonos en una masa de control, una masa determinada del fluido.
Por su propia definición, esta masa no varía. La masa M es igual a la integral de volumen de
la densidad. La región del espacio ocupada por la masa de control,
Vm(t), puede
cambiar con el tiempo, pero la masa es fija:
(d⁄dt) M = (d⁄dt) ∫∫∫Vm(t) ρ dV = 0.
Sólo está indicada la dependencia explícita del tiempo del
volumen Vm(t),
pero la densidad también depende del tiempo y del espacio.
La omisión está hecha con el fin de hacer la notación
más simple y se aplicará por igual al campo de velocidades
v (de módulo v), al campo de presión p y al campo de energía interna por unidad
de masa e.

Campo de velocidades: en cada punto del espacio y en cada instante
del tiempo podríamos poner un minúsculo anemómetro imaginario y
medir la velocidad del fluido allí. El conjunto de estas velocidades,
cada una con su posición espaciotemporal, es el campo de velocidades.
La figura muestra, en dos dimensiones, una visión cualitativa de
los vectores de velocidad alrededor de un torbellino.
Si aplicamos el teorema
del transporte de Reynolds al volumen V (de frontera S y normal a la frontera n), podemos expresar la derivada de la
masa de una masa de control (que es nula porque la masa no varía)
con lo que pasa en el volumen que ocupa:
(d⁄dt) M =
∫∫∫V (∂⁄∂t) ρ dV +
∫∫S ρ v ⋅ n dS
= 0.
Ésta es la ecuación de la conservación de la masa en forma
integral para un volumen de control fijo.
Ecuación de la cantidad de movimiento
La masa de control está sometida a fuerzas exteriores. Por
hipótesis, estas fuerzas son sólo las de la presión aplicada en
su contorno Sm(t).
La segunda ley de Newton, aplicable a la masa de control, dice que la
cantidad de movimiento P varía en el
tiempo con la fuerza aplicada. La cantidad de movimiento de la masa
de control resulta de integrar la cantidad de movimiento por unidad
de volumen ρv por todo
el volumen ocupado por la masa de control. Con estas condiciones,
la segunda ley de Newton queda así:
(d⁄dt) P
= (d⁄dt) ∫∫∫Vm(t) ρv dV
= −∫∫Sm(t) p n dS.
La integral de la presión tiene un signo negativo porque
la presión, que siempre actúa en la direccion perpendicular a
la superficie, es positiva cuando apunta hacia el interior del
volumen (es decir, cuando hay compresión) y la normal n está definida como positiva hacia
el exterior.
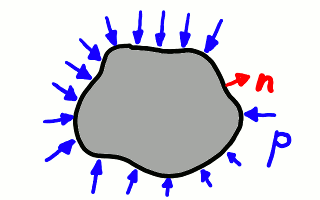
Esfuerzos de presión (flechas azules) sobre un elemento fluido
(mancha gris).
Podemos aplicar el teorema del transporte de Reynolds a cada
una de las componentes de la velocidad, con lo que obtenemos tres
ecuaciones. Con el fin de ser más escuetos, podemos expresar las
ecuaciones de forma vectorial. Queda lo que sigue:
(d⁄dt) P
= ∫∫∫V (∂⁄∂t) (ρv) dV
+ ∫∫S (ρv) v ⋅ n dS
= −∫∫S p n dS.
Ésta es la ecuación de la cantidad de movimiento escrita en forma
integral para un volumen de control fijo.
Ecuación de la energía
La última ecuación que necesitamos es primer
principio de la termodinámica, que en una de sus formas dice
que la energía total E, suma de la
energía interna y la energía mecánica, es igual a la suma del calor
y el trabajo aportados por el exterior. Por hipótesis, no hay más
energía mecánica en el fluido que la cinética. La energía total
será, por lo tanto, la integral de las energías interna y cinética
por unidad de volumen en la región ocupada por la masa de control.
También por hipótesis, no hay calor aportado por el exterior (que
se transmitiría por conducción o radiación) y el trabajo es el de la
única fuerza, la de presión. La variación de la energía total con
el tiempo es igual a la potencia de estas fuerzas de presión. Por
lo tanto, obtenemos esta expresión de la ecuación de la energía:
(d⁄dt) E
= (d⁄dt) ∫∫∫Vm(t) (ρe+ρv2⁄2) dV
= −∫∫Sm(t) p n ⋅ v dS.
El criterio de signos, como antes, nos obliga a poner un menos
delante del término de la presión.
Ahora apliquemos, como antes, el teorema del transporte de Reynolds
para ver lo que pasa en un volumen de control fijo. Nos queda
esta ecuación:
(d⁄dt) E =
(d⁄dt) ∫∫∫V (ρe+ρv2⁄2) dV
+ ∫∫S (ρe+ρv2⁄2) v ⋅ n dS
= −∫∫S p n ⋅ v dS.
Ésta es la ecuación de la energía escrita en forma integral
para un volumen de control fijo.
Todo junto
Reunamos las ecuaciones de la conservación de la masa, de la cantidad de movimiento y de la energía. Si introducimos las magnitudes tensoriales I (el tensor unitario tal que I ⋅ n para cualquier vector n) v⊗v (el producto tensorial de la velocidad por sí misma), podemos escribir las ecuaciones de Euler completamente en forma de conservación: lo que varía una magnitud en un volumen es compensado por unos flujos a través de la frontera de este volumen.
∫∫∫V (∂⁄∂t) ρ dV + ∫∫S ρ v ⋅ n dS = 0
∫∫∫V (∂⁄∂t) (ρv) dV + ∫∫S (ρv⊗v+pI) ⋅ n dS = 0
∫∫∫V (∂⁄∂t) (ρe+ρv2⁄2) dV + ∫∫S (ρe+ρv2⁄2+p) v ⋅ n dS = 0.
La anterior forma de expresar las ecuaciones de Euler es muy útil y general. Vale para situaciones en las que hay superficies de discontinuidad (como las ondas de choque) que otras formulaciones, debido a que asumen cierta suavidad de las soluciones, no pueden modelar. Varias familias de métodos numéricos de volúmenes finitos de alta resolución para resolver problemas de mecánica de fluidos sin viscosidad están basados en esta forma de expresar las ecuaciones de Euler.
Tenemos tres ecuaciones, pero hay cuatro campos incógnita (el de densidad, el de velocidad, el de presión y el de energía interna). La ecuación adicional para resolver el problema, la ecuación de cierre, es una ecuación constitutiva que suele relacionar presión, densidad y energía interna. En el caso de gases, es a menudo de aplicación la ley de los gases ideales junto con una relación lineal entre la temperatura y la energía interna. En el caso de líquidos ideales, la densidad es constante, lo que elimina trivialmente una de las incógnitas y permite resolver primero las ecuaciones de la conservación de la masa y de la cantidad de movimiento y, después, la de la energía.
Con las condiciones iniciales y de contorno adecuado y la ecuación constitutiva adecuada la aplicación de las ecuaciones de Euler a volúmenes arbitrarios permite resolver el problema de la evolución de un fluido simple no viscoso. El lector avispado podrá darse cuenta de que, en realidad, si nos encontramos superficies de discontinuidad, entonces hay soluciones múltiples. Esto se debe a las simplificaciones que hemos hecho al no tener en cuenta fenómenos difusivos como la viscosidad. Veremos más adelante cómo podemos usar el segundo principio de la termodinámica para elegir la solución adecuada sin necesidad de emplear modelos matemáticos más complicados.
Las ecuaciones de Euler son una herramienta de trabajo que usan a diario aerodinamistas de todo el mundo para producir vehículos más rápidos, seguros y eficientes.
Otros artículos sobre las ecuaciones de Euler de la mecánica de fluidos
- Las ecuaciones en forma diferencial de conservación.
- Las ecuaciones en forma diferencial de no conservación.
Categorías: Física, Matemáticas
Permalink: https://sgcg.es/articulos/2011/10/22/ecuaciones-de-euler-de-la-mecanica-de-fluidos-1/
