El problema de la catenaria
2012-05-20

Curva catenaria descrita por una cadena colgante.
La catenaria es la curva que describe una cuerda inextensible a tracción, perfectamente flexible a flexión y de sección constante al colgar entre sus dos extremos sometida a su propio peso en un campo gravitatorio uniforme. Muchos objetos como hilos, cuerdas, cables y cadenas pueden ser descritos satisfactoriamente en muchas ocasiones mediante el modelo de la catenaria (cuyo nombre viene de «cadena»).
El problema de determinar la forma de la catenaria es un clásico de la mecánica aplicada. Veamos cómo resolverlo.
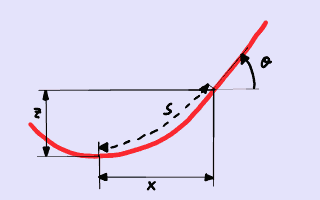
Sistema de coordenadas del problema.
Definamos algunas propiedades para nuestra cuerda. La densidad del material es ρ, el área de la sección transversal es A, la aceleración gravitatoria es ρ, la longitud de arco a lo largo de la cuerda es s, la coordenada horizontal a lo largo de la cuerda es x, la coordenada vertical a lo largo de la cuerda es z, el ángulo que forma con la horizontal un segmento elemental de cuerda es θ y la fuerza de tracción en una sección transversal de cuerda es T.
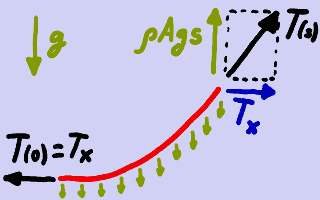
Equilibrio de fuerzas.
En el equilibrio, la cuerda mantiene su forma. El peso queda equilibrado por la fuerza de tracción. Como la fuerza de gravedad va según la vertical, la proyección vertical de la fuerza de tracción depende del peso que sostiene debajo de sí cada punto de la cuerda, pero la proyección horizontal es constante. Si llamamos Tx a dicha proyección horizontal, nos queda la siguiente igualdad:
T cos(θ) = Tx.
En cuanto a la proyección vertical, ésta adopta la siguiente forma si tomamos como origen de arcos s = 0 el punto más bajo de la cuerda:
T sin(θ) = ρ A g s.
La tangente del ángulo θ que forma con la horizontal un segmento elemental de cuerda es, por lo tanto,
dz ⁄ dx = tan(θ) = sin(θ) ⁄ cos(θ) = (ρ A g ⁄ Tx) s = k s.
Introducimos la constante k para aligerar la notación.
Unas nociones elementales de geometría diferencial nos dicen que el elemento diferencial de longitud de arco ds es el siguiente:
ds = √(1 + dz ⁄ dx) dx.
Estas dos últimas ecuaciones junto con una condición inicial adecuada (digamos x = 0 en el origen de arcos s = 0) son suficientes para relacionar la coordenada horizontal con la longitud de arco. En efecto queda una ecuación cuya integral es inmediata:
ds ⁄ dx = √(1 + k2 s2)
⇒ k s = |sinh(k x)|.
El valor absoluto se toma para que la longitud de arco sea siempre positiva.
Si introducimos el último resultado en la ecuación de la pendiente e integramos con la condición inicial y = 0 para x = 0, queda el siguiente resultado, la forma explícita de la curva catenaria:
z = [cosh(k x) − 1] ⁄ k.
Curva catenaria.
La constante k es muy molesta, pero podemos determinarla fácilmente si conocemos la longitud l de la cuerda, la distancia vertical Δz entre los extremos y la distancia horizontal Δx entre los extremos. De las ecuaciones que relacionan la posición vertical z y la longitud de arco s con la posición horizontal x, tras un poco de álgebra, sale lo siguiente:
[l2 − (Δz)2] k2 = 4 [sinh(k Δx ⁄ 2)]2.

Geometría general del problema.
Si introducimos el parámetro dinámico ξ ≡ k Δx ⁄ 2 y el parámetro geométrico η ≡ √[(l ⁄ Δx)2 − (Δz ⁄ Δx)2], queda una función uniparamétrica muy conveniente que podemos pintar una sola vez para calcular gráficamente el parámetro de la catenaria:
η = sinh(ξ) ⁄ ξ.
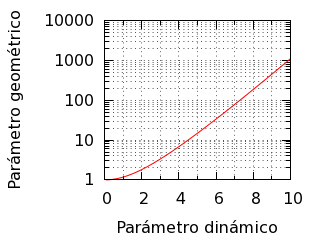
Parámetros de la catenaria. El parámetro dinámico es la
variable ξ de la anterior
ecuación y el parámetro geométrico es la variable η de la anterior ecuación.
Categorías: Física, Matemáticas
Permalink: https://sgcg.es/articulos/2012/05/20/el-problema-de-la-catenaria/
