¿Puede romperse por su propio peso un cable tendido?
2012-05-21
Como continuación del artículo anterior sobre la curva catenaria que describen con buena aproximación cables, cuerdas, hilos y cadenas al colgar entre sus dos puntos extremos, veremos hoy en qué condiciones uno de estos elementos no podría sostener su propio peso y acabaría rompiéndose.
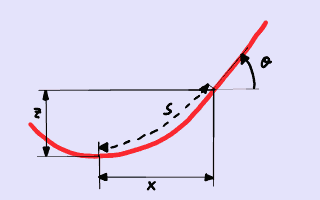
Sistema de coordenadas.
Recordemos la ecuación de la curva catenaria en coordenadas cartesianas. La coordenada horizontal es x, la coordenada vertical es z y la longitud de arco es s. Para concretar, fijamos el origen de coordenadas en el punto en el punto de mínima altura de la curva catenaria. El origen es sólo una referencia matemática y bien podría suceder que tal punto quedara fuera de la cuerda al acabarse ésta antes. Las ecuaciones son las siguientes:
z = [cosh(k x) − 1] ⁄ k,
s = |asinh(k x)| ⁄ k.

Geometría general de la catenaria.
La constante k está determinada por la geometría general: depende de la distancia vertical Δz entre los puntos extremos, la distancia horizontal Δx entre los puntos extremos y la longitud l de la cuerda. En concreto, vimos que el parámetro adimensional geométrico ξ ≡ k Δx ⁄ 2 y el parámetro adimensional dinámico η ≡ √[(l ⁄ Δx)2 − (Δz ⁄ Δx)2] tienen una relación funcional sencilla, de modo que si se conoce el parámetro η que sólo depende de la geometría, se deduce inmediatamente el parámetro ξ y, a partir de éste, el parámetro k:
η = sinh(ξ) ⁄ ξ.
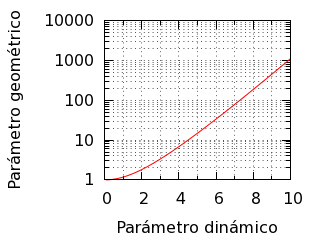
Parámetros adimensionales.
El parámetro adimensional geométrico η depende de las proporciones de las distancias horizontal Δx y vertical Δz entre los puntos extremos y la longitud l de la cuerda; si escalamos todo mientras mantenemos las proporciones (pasamos de los valores Δx, Δz y l a los valores c Δx, c Δz y c l), entonces el parámetro adimensional geométrico η se conserva inalterable, el parámetro adimensional dinámico ξ también se conserva inalterable y, finalmente el parámetro k de la curva escala como k = 2 ξ ⁄ Δx, es decir, es inversamente proporcional al tamaño de la cuerda para unas proporciones dadas.
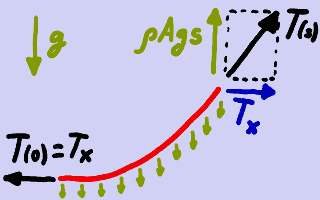
Equilibrio de fuerzas.
Vimos que la cuerda equilibra su peso mediante fuerzas internas de tracción. La fuerza de tracción T está dirigida según la dirección tangente a la cuerda y se extrae de los resultados del artículo anterior como
T = (ρ A g) √[(1 ⁄ k)2 + s2].
A la hora de analizar si se rompe o no la cuerda, lo interesante no es la fuerza resultante de tracción, sino la tensión σ = T ⁄ A. Vemos que la fuerza de tracción crece con la longitud de arco, así que será máxima en el extremo más alto, cuya longitud de arco smáx medida desde el origen de coordenadas es conocida. La tensión máxima σmáx es, por lo tanto, la siguiente:
σmáx = (ρ g) Δx √[1 ⁄ (2 ξ)2 + (smáx ⁄ Δx)2].
Hemos utilizado la relación entre el parámetro de la curva k y el parámetro adimensional dinámico ξ que sólo depende de las proporciones y no del tamaño absoluto.
Un buen modelo de resistencia de la cuerda consiste en que ésta se rompe cuando la tensión máxima σmáx supera cierto valor S que depende del material y de la construcción de la propia cuerda. Vemos que la tensión máxima es independiente del área A de la sección transversal, así que hacer que ésta crezca (con lo que aumenta el peso de la cuerda) no tiene efecto cuando es válido el modelo de cuerda inextensible a tracción y perfectamente flexible a flexión. Las otras maneras de aumentar el peso de la cuerda consisten en hacer crecer la densidad ρ (cambiar de material o construcción, pero esto probablemente cambiará la resistencia S), la aceleración gravitatoria g (¡irse muy lejos!) o hacer crecer el tamaño absoluto de la cuerda (representado aquí por la distancia horizontal Δx cubierta). El peso total aumenta linealmente con cualquiera de estas variables y la tensión máxima también aumenta linealmente con cualquiera de estas variables. Si nos limitamos a la geometría, vemos que, para unas proporciones «macroscópicas» (distancias a salvar y longitud de la cuerda) dadas, la cuerda puede romperse si se hace crecer mucho la dimensión absoluta «macroscópica», pero es insensible a la dimensión «microscópica» (el área de la sección transversal).
Categorías: Física, Matemáticas
Permalink: https://sgcg.es/articulos/2012/05/21/puede-romperse-por-su-propio-peso-un-cable-tendido/
