Jugando con autómatas celulares (11)
2013-09-08
Hace varios artículos, planteamos un interesante proyecto: una pequeña biblioteca para construir autómatas celulares. Los autómatas celulares son unas estructuras matemáticas muy curiosas: retículos de celdas que van cambiando de un estado a otro y que pueden, a partir de reglas sencillas, exhibir complejísimos comportamientos emergentes. Como práctica, nuestra biblioteca estará hecha en Scheme R5RS y en Python 2. El enfoque es funcional porque el problema se presta mucho a ello. No nos preocuparemos tanto por hacer un código especialmente rápido como por hacerlo claro y conciso.
Tenemos una biblioteca de autómatas celulares que empieza a ser muy potente. ¡Probemos unos pocos autómatas elementales!
Regla 90
Vamos a repetir el experimento de la regla 90 que
hicimos en
el segundo artículo de la serie. Partiremos, como aquella vez, de
una celda activa (de estado 1) centrada y rodeada de celdas inactivas;
imprimiremos asteriscos para mostrar celdas activas y espacios en
blanco para mostrar celdas inactivas. El código es así:
(interactive-step (wolfram-rule 90)
(append (repeat 0 10) (list 1) (repeat 0 10))
cyclic-elementary-neighbourhoods
(lambda (cells)
(translate-and-display-1d cells " *")))
Esto es en Scheme. En Python, es así:
interactive_step(wolfram_rule(90),
[0] * 10 + [1] + [0] * 10,
cyclic_elementary_neighbourhoods,
lambda cells: translate_and_display_1d(cells, " *"))
En cualquiera de los dos casos, tras unas cuantas iteraciones,
reproducimos una forma que recuerda a un triángulo de Sierpinski. Es
como si hubiéramos llegado al final del fractal en un mundo discreto y
a partir de allí, de una esquinita, nos alejáramos más y más. Las
primeras líneas tienen este aspecto:
*
* *
* *
* * * *
* *
* * * *
* * * *
* * * * * * * *
* *
* * * *
* * * *
Esto tiene la siguiente pinta visto desde lejos:
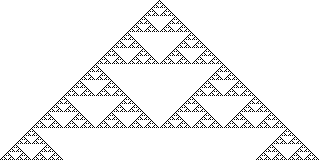
Ejemplo de evolución mediante la regla 90.
Regla 30
La regla 30 produce hermosos resultados de apariencia aleatoria.
Si partimos, como antes, de un punto central,
(interactive-step (wolfram-rule 30)
(append (repeat 0 10) (list 1) (repeat 0 10))
cyclic-elementary-neighbourhoods
(lambda (cells)
(translate-and-display-1d cells " *"))),
el resultado no es muy impresionante:
*
***
** *
** ****
** * *
** **** ***
** * * *
** **** ******
** * *** *
** **** ** * ***
** * * **** ** *
Esto es muy pequeño. La siguiente imagen tiene más líneas:

Ejemplo de evolución mediante la regla 30.
Regla 110
En la regla 110, el estado de la celda a la derecha es ignorado.
Podemos probar con una celda encendida en el punto situado más a la
derecha:
(interactive-step (wolfram-rule 110)
(append (repeat 0 19) (list 1))
cyclic-elementary-neighbourhoods
(lambda (cells)
(translate-and-display-1d cells " *")))
Las primeras generaciones salen así:
*
**
***
** *
*****
** *
*** **
** * ***
******* *
** ***
*** ** *
** * *****
***** ** *
** * *** **
*** **** * ***
** * ** ***** *
******** ** ***
** **** ** *
*** ** * *****
** * *** **** *
Visto desde más lejos, tenemos el siguiente resultado:

Ejemplo de evolución mediante la regla 110.
Regla 11
Esta regla da lugar a patrones ondulatorios que avanzan hacia la derecha como ondas planas. La siguiente imagen muestra el resultado a partir de un estado inicial aleatorio:

Ejemplo de evolución mediante la regla 11.
Otros artículos de la serie
- Introducción.
- Pequeño autómata de demostración.
- Función para crear reglas deterministas.
- Funciones para sacar por pantalla las listas de celdas.
- Funciones auxiliares útiles.
- Más funciones auxiliares útiles.
- Funciones para trabajar con mallas cartesianas.
- Extracción de vecinos en mallas cartesianas cíclicas
- Funciones para crear autómatas unidimensionales elementales.
- Funciones para crear generaciones sucesivas de autómatas cómodamente.
- Funciones para imprimir autómatas bidimensionales cartesianos.
- Juego de la vida de Conway.
- Funciones para trabajar con autómatas no deterministas.
- Autómata no determinista: modelo del incendio forestal.
- Autómatas de segundo orden.
- Mejora del rendimiento mediante memoización.
- Más pequeñas modificaciones para acelerar notablemente el código.
- Salida de imágenes.
Categorías: Informática
Permalink: https://sgcg.es/articulos/2013/09/08/jugando-con-automatas-celulares-11/
