Modelando la influencia del tamaño del pecho en las molestias al correr y saltar
2015-01-12
Varios divulgadores científicos han propuesto escribir articulillos eso, divulgativos, relacionados con el busto humano: el desafío #lunesTetas. Aquí va mi aportación.
Occidente adora la estética del pecho femenino, pero las poseedoras de un busto generoso saben que estas cosas tienen sus inconvenientes al correr y saltar sin una sujeción adecuada. Vamos a plantear un modelo físico elemental (lo que en inglés se conoce como «toy model») para hacernos una idea cualitativa de cómo podrían comportarse las molestias durante la actividad física en función del tamaño del pecho.
Modelo elemental
El pecho de una mujer se comporta como un sólido viscoelástico. Muestra tendencia a recuperar su forma, pero esta fuerza de recuperación depende del ritmo de deformación. Hay múltiples maneras de modelar este comportamiento, pero una de las más sencillas (aunque con ciertas limitaciones) consiste en colapsar todo el movimiento en una sola variable, el desplazamiento x(t) de un punto representativo en función del tiempo t, y asumir que la fuerza de recuperación es la suma de una elástica lineal (como un muelle) y una de amortiguamiento viscoso también lineal (como un amortiguador). El desplazamiento está medido con respecto al tórax, que experimenta un movimiento oscilatorio con una aceleración a(t). Este modelo pierde validez rápidamente en diversas circunstancias, entre las que se incluyen los movimientos especialmente amplios y pendulares, en los que aparecen fenómenos no lineales importantes.
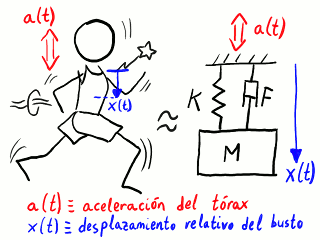
Oscilador armónico amortiguado con excitación en la base como
modelo del desplazamiento del busto al correr.
Este oscilador armónico tiene:
- una rigidez K que relaciona linealmente la fuerza de recuperación elástica (que se opone al desplazamiento del pecho y tiende a colocarlo en una posición neutral) con el desplazamiento;
- un amortiguamiento F que relaciona linealmente la fuerza de amortiguamiento (que se opone a la velocidad de deformación del pecho y tiende a frenarlo) con la rapidez del desplazamiento;
- una masa M, la inercia del pecho.
La ecuación diferencial es la siguiente:
M (d2⁄dt2) x(t) + F (d⁄dt) x(t) + K x(t) = −M a(t).
Introducimos unas variables adicionales:
- la pulsación natural ω0 ≡ √(K ⁄ M);
- el factor de amortiguamiento ζ ≡ F ⁄ (2 M ω0).
Con estas nuevas variables, tras dividir por la masa M, la ecuación diferencial queda así:
(d2⁄dt2) x(t) + 2 ζ ω0 (d⁄dt) x(t) + ω02 x(t) = −a(t).
Representación fasorial
Vamos a asumir que la aceleración sigue una ley sinusoidal periódica de pulsación ω. Usaremos el viejo truco de expresarla como una exponencial compleja (lo que se conoce como una representación fasorial); siempre podemos descartar la parte imaginaria al final:
a(t) ≡ A ei ω t.
Para fijar el origen de fase, la amplitud A es un número real.
Tras mantener la actividad durante mucho tiempo, la respuesta transitoria no se nota y solamente tenemos una respuesta que también es sinusoidal de la misma frecuencia que la excitación:
x(t) ≡ X ei ω t.
Esta formulación permitirá transformar la ecuación diferencial en una ecuación algebraica. La amplitud de la respuesta X es en general un número complejo cuyo argumento es el desfase frente a la entrada.
La ecuación diferencial queda de la siguiente manera tras introducir las formas funcionales de arriba:
(−ω2 + 2 i ζ ω0 ω + ω02) X ei ω t = −A ei ω t.
La amplitud compleja de la respuesta sale de despejar:
X = −A ⁄ (ω02 − ω2 + 2 i ζ ω0 ω).
Vamos a asumir que las molestias que experimenta nuestra atleta son directamente proporcionales a la fuerza de reacción mientras su pecho rebota. En este modelo de juguete, la fuerza de reacción es igual a la suma de la fuerza de recuperación elástica y la fuerza de amortiguamiento viscoso. De nuevo con el truco algebraico de antes, a sabiendas de que la reacción también será sinusoidal de la misma frecuencia, la amplitud compleja es
R = K X + i ω F X = M (ω2 X − A) = −M A (ω02 + 2 i ζ ω0 ω) ⁄ (ω02 − ω2 + 2 i ζ ω0 ω).
Influencia del tamaño del pecho
Vamos a introducir otra simplificación enorme: asumimos que podemos colapsar la geometría del pecho en un único parámetro relevante: una longitud l que representa el tamaño. Para fijar ideas, tomamos que las constantes del oscilador armónico amortiguado están relacionadas con el tamaño de la siguiente manera (que sale de asumir un modo de cortadura pura con amortiguamiento proporcional a la rigidez):
- M ≡ M0 l3;
- F ≡ F0 l;
- K ≡ K0 l.
La frecuencia natural y el factor de amortiguamiento se derivan de las constantes anteriores:
- ω0 = √(K0 ⁄ M0) ⁄ l;
- ζ = F0 ⁄ [2 √(K0 M0) l].
Ahora queda introducir estas expresiones en la fuerza de reacción. Esta fuerza es directamente proporcional a la aceleración de entrada, así que podemos calcular la respuesta con aceleración unidad y escalarla para cualquier aceleración dada. Además de esto, el análisis dimensional nos dice que podemos redefinir las unidades de medida y asignar el valor 1 a 3 constantes diferentes; nos libraremos de la pulsación de los saltos ω, la constante de la inercia M0 y la constante de la rigidez K0. Con esta redefinición, la fuerza de reacción queda así:
|R| = √{[(1+F02) l6] ⁄ [l4 − 2 l2 + (1+F02)]};
arg(R) = atan{[F0 l2] ⁄ [l2 − (1+F02)]}.
La constante del amortiguamiento, que es algo que habría que medir para ajustar el modelo a la realidad dentro de cierto rango de tamaños de pecho, influye en el comportamiento cualitativo de la fuerza de reacción, que tiene un máximo local cuando el amortiguamiento es bajo. Este máximo local indica la presencia de un efecto de resonancia: un pecho de cierto tamaño concreto tiene una frecuencia de resonancia que más o menos coincide con la frecuencia de los rebotes de la carrera o de los saltos, así que las molestias son máximas localmente y se reducirían con un pecho ligeramente más pequeño o ligeramente más grande. Veremos que esta resonancia es más una curiosidad matemática que un problema real.
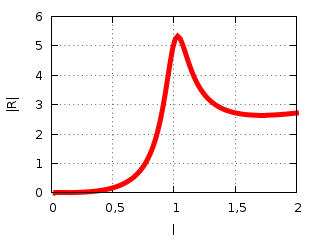
Magnitud de la fuerza de reacción en función del tamaño del pecho
para un amortiguamiento bajo que bien podría no tener nada que ver con
el real. El máximo local se da con un tamaño de pecho tal que su
frecuencia de resonancia más o menos coincide con la de los rebotes de
la carrera o de los saltos. Este máximo local es difícil de alcanzar
en la práctica.
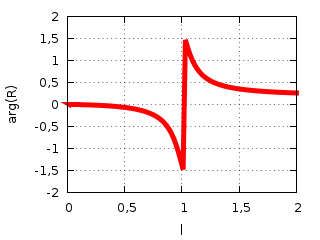
Desfase de la fuerza de reacción en función del tamaño del pecho
para un amortiguamiento bajo que bien podría no tener nada que ver con
el real. La singularidad no es más que un efecto del valor principal
usado para el argumento (por haberlo elegido
entre −π
y π) y se da con un tamaño de pecho tal
que su frecuencia de resonancia más o menos coincide con la de los
rebotes de la carrera o de los saltos: un pecho más pequeño reacciona
con retardo frente a la excitación, mientras que uno más grande se
adelanta (o se retrasa tanto que queda más cerca de estar adelantado
al movimiento periódico). Esta resonancia es difícil de alcanzar en
la práctica.
Salvo por el fenómeno de la resonancia, la tendencia general es a aumentar la fuerza de reacción (y, con ello, las molestias) con el tamaño del pecho. La solución, por supuesto, consiste en usar un sujetador deportivo, que aumenta la rigidez (y, con ello, la frecuencia de resonancia), lo que reduce la reacción, que además se reparte de una manera más benigna.
La resonancia no es fácil de alcanzar en la práctica
Dentro del régimen razonablemente elástico, el busto de una mujer tiene una frecuencia natural en el entorno de algunos Hz (una pulsación natural ω0 de algunas decenas de rad s−1). En general, podemos asumir que la frecuencia de los rebotes al correr o al saltar es más baja y no se llega al punto de resonancia. Los armónicos de orden superior pueden notarse, pero su amplitud es pequeña. Un pecho muy grande puede tener su frecuencia de resonancia próxima a la de los pasos, pero antes se producen fenómenos no lineales importantes que anulan la validez cuantitativa de este análisis (aunque no el hecho de que la actividad física vigorosa sin una buena sujeción puede causar dolor).
En los casos más comunes, no se alcanza la resonancia y, por lo general, un busto voluminoso sufre más molestias que uno pequeño. Los sujetadores deportivos sirven para paliar este problema.
Categorías: Física
