Diseño de una estantería librería (2)
2015-01-21
Ayer planteamos el proyecto de diseñar y construir estantería para colocar libros. Entonces establecimos las dimensiones básicas de la estantería; hoy dimensionaremos las baldas.
Los tableros de aglomerado vienen en varios espesores diferentes. Interesa escoger el espesor más pequeño que garantice la correcta resistencia de la estructura, ya que los tableros delgados son más baratos y ligeros que los gruesos. Anticipamos que una balda típica trabaja más que nada como una viga simplemente apoyada en sus extremos y cargada a flexión.
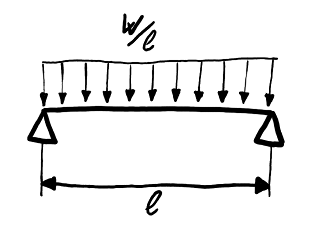
Esquema del modelo de la balda: una viga simplemente apoyada con
carga uniforme.
La balda tiene una luz l = 80 cm y sobre ella reposa un peso W uniformemente distribuido. Las tensiones dimensionantes son las que equilibran el momento flector en la sección central: M = W l ⁄ 8.
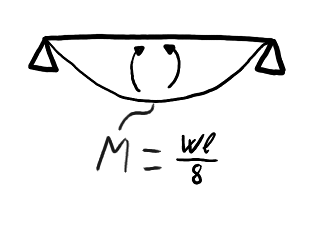
Distribución del momento flector a lo largo de la balda.
Antes de que el aglomerado empiece a romperse, aparecen esfuerzos de tracción y compresión que equilibran el momento flector como en la figura siguiente:
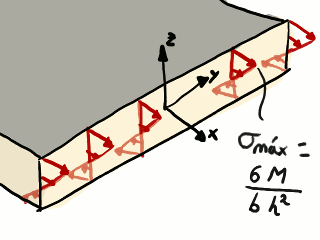
Distribución de esfuerzos en la sección central de la balda.
Ahora nos centraremos en la sección transversal de la balda, que tiene una profundidad o ancho b = 30 cm y un espesor h que es nuestra variable de diseño.
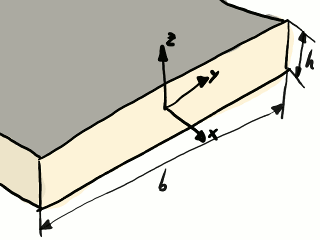
Geometría de la sección transversal de la balda.
El esfuerzo máximo es σmáx = 6 M ⁄ (b h2). Es fácil comprobar que el momento de esta distribución lineal equilibra el momento flector:
∫−b⁄2≤y≤b⁄2dy ∫−h⁄2≤z≤h⁄2dz σmáx ⋅ (2 z ⁄ h) = M.
La balda empieza a fallar en las fibras más extremas cuando se alcanza la resistencia a la flexión del material, σr, que para un aglomerado de densidad media ronda los 12 MPa. El peso máximo que puede soportar la balda sale de sustituir variables:
W = (4 ⁄ 3) (b h2 ⁄ l) σr.
Esto ya duplica el máximo peso esperado de unos 300 N con un espesor h = 1 cm. Por lo tanto, parece razonable salir adelante con este espesor, al menos por lo que se refiere a la resistencia de las baldas.
Categorías: DIY
Permalink: https://sgcg.es/articulos/2015/01/21/diseno-de-una-estanteria-libreria-2/
