Diseño de una estantería librería (9)
2015-02-21
Continuamos con el diseño de una estantería librería colocada en un espacio libre sobre un mueble aparador. Ayer empezamos a analizar las uniones atornilladas de las escuadras a los paneles. Hoy terminamos el análisis.
Vimos que, en principio, la carga a la que están sometidas las baldas laterales, que están en voladizo, no puede arrancar los tirafondos directamente, ya que las escuadras tienden a pegarse al panel y repartir directamente la carga, sin tirar de los tornillos de forma significativa. Llegamos a esta conclusión al asumir que los tirafondos restringen las escuadras a la hora de alejarse del panel, pero no a la hora de inclinarse: es decir, al asumir que los tirafondos actúan como apoyos simples. En el otro extremo de rigidez frente a rotaciones, podríamos suponer que el primer tirafondos recibe el momento flector completo, en cuyo caso puede incrustarse en la madera como en la siguiente figura:
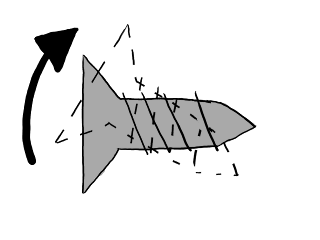
Posible modo de fallo de la unión atornillada. El tirafondos, muy
rígido y resistente, se abre camino a través del aglomerado rotando
bajo un momento flector.
La distribución de tensiones en la interfaz entre el tornillo y el aglomerado es complicada, pero podemos estimar rápidamente el orden de magnitud del momento flector que provocaría que el tirafondos comenzara a incrustarse. Con una balda de longitud L = 20 cm cargada con un peso W, el momento flector soportado por tornillo es del orden de
M ≈ O(W L).
El tornillo empieza a abrirse paso a través del aglomerado al alcanzar la resistencia σ ≈ 10 MPa del material. Con un diámetro medio d = 1,5 mm y una longitud atornillada en la madera l = 7 mm, el máximo momento flector que podría transmitir un tirafondos antes de que el aglomerado cediera sería
M ≈ O(l2 d σ).
Si igualamos ambos momentos, vemos que el peso máximo que puede colgarse antes de agotar el material es del orden de W ≈ O(1 N). Una vez se alcanza la resistencia, el tornillo ya no puede transmitir más momentos flectores y el comportamiento pasa a asemejarse al de la viga simplemente apoyada que vimos ayer (un poco más complejo debido a que el aglomerado se deforma ligeramente). En la práctica, estas escuadras tan pequeñas serán lo primero en fallar.
Categorías: DIY
Permalink: https://sgcg.es/articulos/2015/02/21/diseno-de-una-estanteria-libreria-9/
