Tensiones o esfuerzos mecánicos (1)
2015-08-12
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. En este artículo y los siguientes veremos en qué consiste.
Fuerzas por unidad de superficie
Los medios continuos que estudiamos son medios materiales, sustancias que interactúan unas con otras mediante fuerzas. Hay fuerzas de largo alcance, como la fuerza de gravedad, pero también hay fuerzas de tan corto alcance que podemos modelarlas como fuerzas de contacto: se producen al tocar un cuerpo con otro.
Imaginémonos un medio continuo. Cortémoslo imaginariamente en dos partes mediante un plano. Cada una de estas partes o subdominios, A y B, es un medio continuo en contacto con la otra parte a través del plano de corte. Más adelante, nos referiremos a la superficie de contacto como S.
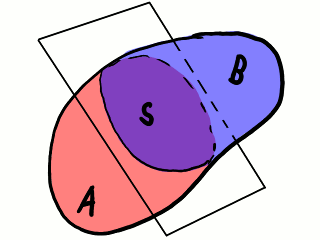
División de un medio continuo en dos partes mediante un plano de
corte.
Uno de los subdominios, A, es objeto de una fuerza de contacto F a través de la superficie de corte S. Por el principio de acción y reacción, el otro subdominio, B, recibe una fuerza de contacto igual y opuesta, −F. Como todas las fuerzas, F es vectorial: tiene una magnitud y una dirección. En general, la dirección de la fuerza de contacto no es necesariamente perpendicular a la superficie de contacto: tiene una componente normal y una componente tangencial.
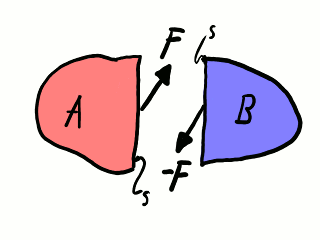
Fuerzas de contacto internas.
Más que las fuerzas totales en una superficie de contacto, nos interesan las fuerzas por unidad de superficie. Antes teníamos una fuerza de contacto F (del subdominio B sobre el subdomio A) aplicada en una superficie de contacto que llamaremos S; la fuerza de contacto promediada por la superficie de contacto es F ⁄ S. Nada nos impide dividir o teselar la superficie de contacto en superficies más pequeñas como si fuera un rompecabezas hecho de múltiples piezas; si lo hacemos, vemos que se aplica una fuerza de contacto a través de cada una de estas piezas de la superficie, de manera que la fuerza de contacto total es igual a la suma de las fuerzas aplicadas en las piezas. De igual manera, en cada pieza hay fuerza por unidad de superficie: la fuerza de contacto en esa pieza dividida por la superficie en esa pieza.
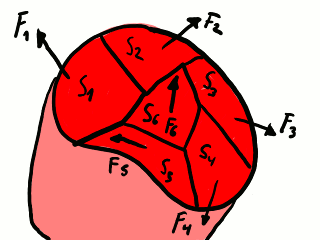
Teselación de un plano de corte.
Si llevamos el proceso al límite, las piezas quedan de un tamaño infinitesimal, cada una rodeando a un punto de la superficie de contacto. A cada uno de estos puntos le corresponde un vector de fuerza por unidad de superficie.
Fijémonos en un punto y hagamos pasar dos planos de corte con orientaciones diferentes por él. En general, no tenemos motivos para asumir que la fuerza por unidad de superficie con el primer plano de corte es igual a la fuerza por unidad de superficie con el segundo plano de corte: la fuerza por unidad de superficie depende del punto en el que la medimos y de la orientación con la que la medimos. La orientación viene dada por el vector normal a la frontera del subdominio, que por convenio apunta hacia el exterior. Si invertimos la orientación es como si pasamos de un subdominio al complementario (del A al B) y la fuerza por unidad de superficie cambia también de sentido. No hace falta definir subdominios para hablar de fuerzas por unidad de superficie: basta indicar el punto en el que se mide y la orientación con la que se mide.
Categorías: Física
Permalink: https://sgcg.es/articulos/2015/08/12/tensiones-o-esfuerzos-mecanicos-1/
