Mayo de 2012
Calendario de artículos de de 2012
| lu | ma | mi | ju | vi | sá | do |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 | |||
El caso de Oracle contra Google y el copyright de las interfaces de programación (2)
2012-05-31
El juez Willian Alsup, quien lleva el caso de Oracle contra Google del que ya hablamos hace unas semanas, acaba de pronunciarse sobre la cuestión del copyright de la estructura, la secuencia y la organización de la interfaz de programación de Java: tal copyright no existe, es decir, la interfaz de programación de Java no está sujeta a copyright dado que es un mero método de operación. Este resultado es notable y puede ser materia a explotar en futuros casos similares. En buena medida, alivia la tremenda inseguridad jurídica que se extendía sobre toda la industria de los programas informáticos como consecuencia de la osada acusación presentada por Oracle.
Categorías: Actualidad, Informática
Portatarjetas transparente improvisado
2012-05-30

Un portatarjetas improvisado con material de oficina.
Tenía un collar con mosquetón hecho para llevar tarjetas de identificación y control de acceso, pero me faltaba el portatarjetas para poder usarlo. Afortunadamente, sí tenía acceso a una lámina de PVC transpartente y unas pocas herramientas con las que pude improvisar un portatarjetas quizá no muy bonito, pero que cumplió con su cometido. La lámina es una cubierta de las que venden en papelerías y tiendas de material de oficina.

Vista trasera del portatarjetas. Son apreciables la solapa abierta
(parte superior más clara) con el ojal, la trabilla (banda central más
oscura) y el bolsillo (cuerpo inferior más oscuro que la solapa y más
claro que la trabilla).
Hay muchas formas de hacer un portatarjetas. Éste tiene un cuerpo con un bolsillo y una solapa de cierre que se mantiene en su sitio por medio de una trabilla. La solapa está achaflanada para hacer más fácil su inserción en la trabilla y tiene un ojal para pasar el mosquetón del collar. Todo el portatarjetas está hecho en dos piezas cortadas en una lámina transparente de PVC y unidas mediante soldadura.
Podemos empezar con una plantilla de papel para darle cómodamente las dimensiones adecuadas a nuestro portatarjetas. Plegamos y cortamos el papel alrededor de nuestra tarjeta hasta darle la forma deseada. Alternativamente, aquí tenemos un diseño que funciona bien:
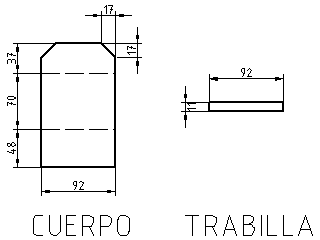
Dimensiones de la plantilla del portatarjetas.
Marcamos la forma en la lámina de PVC y recortamos las piezas. Plegamos la del cuerpo para hacer el bolsillo.
Hay que unir los laterales para que el portatarjetas mantenga su forma y no pueda escaparse su contenido. Basta con solapar los bordes y presionarlos con cuidado con la punta caliente de un soldador eléctrico de unos 20 W o 30 W. Podemos poner un trozo de papel en el interior del bolsillo del portatarjetas para limitar el ancho de la soldadura y así evitar hacer un bolsillo demasiado estrecho para nuestra tarjeta.
Ahora hay que unir la trabilla que sirve para mantener la solapa cerrada. Usamos la misma técnica: colocamos la trabilla en el lugar adecuado sobre el cuerpo del portatarjetas y presionamos en los extremos con el hierro de soldar caliente para realizar una buena unión.
Para terminar, plegamos la solapa y marcamos el lugar donde queremos hacer el ojal para pasar el mosquetón. Aplicamos allí la punta caliente del hierro de soldar hasta hacer un agujero redondo y pasante. Le damos la vuelta al portatarjetas y abrimos bien el agujero por el otro lado. Ya tenemos listo nuestro portatarjetas.

Elaboración del ojal.
Categorías: DIY
Permalink: https://sgcg.es/articulos/2012/05/30/portatarjetas-transparente-improvisado/
Skate spinner
2012-05-27

Spinner en acción visto de frente.
Un skate spinner (o spinner a secas) es un artefacto que sirve para que los patinadores practiquen posiciones de rotación cuando no están patinando. El spinner es una plataforma del tamaño adecuado para apoyar en ella un pie; tiene una cara plana (en la que se pone el pie) y una cara redondeada convexa (el rocker) que está en contacto con el suelo. Como la superficie de contacto con el suelo del rocker es pequeña y está centrada en un punto, la fricción es muy poco efectiva para frenar la rotación y, con un pequeño impulso, el usuario del spinner puede entrar en una pirueta duradera.
He aquí un spinner realizado en ABS con una máquina doméstica de prototipado rápido (una MakerBot Thing-o-Matic en este caso).
Geometría del spinner
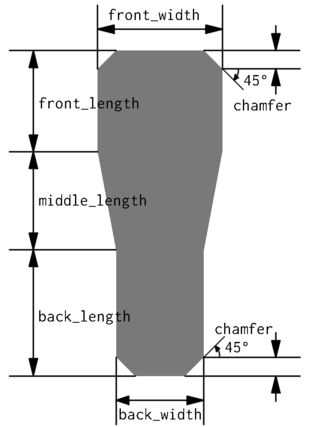
Vista en planta. Las etiquetas de las cotas son los nombres
de los parámetros en el modelo de OpenSCAD.
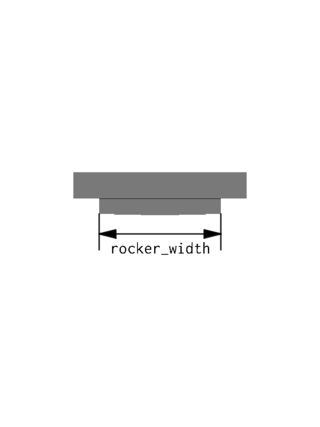
Vista en alzado. Las etiquetas de las cotas son los nombres
de los parámetros en el modelo de OpenSCAD.
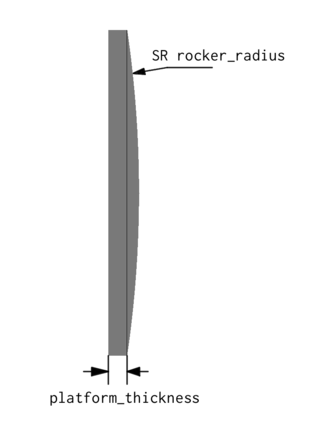
Vista lateral. Las etiquetas de las cotas son los nombres
de los parámetros en el modelo de OpenSCAD.
Nuestro aparato de entrenamiento tendrá la forma idealizada de un pie. Su dimensión longitudinal puede estar en torno a los 26 cm y haremos que sea más ancho en la parte delantera que en la trasera. El radio del rocker puede estar próximo al metro. La sección transversal tiene una pared y un núcleo de panal de abeja como en la figura:

Sección transversal del spinner en pleno proceso
de fabricación.
La sección es hueca. Esto es así por motivos de ahorro. Si queremos que el spinner sea rígido y resista nuestro peso sin romperse, es más efectivo poner el material en en los extremos superior e inferior de la sección que en su centro. De esta manera, la sección transversal es hueca y tiene una pared con cierto espesor. Ahora bien, debido a la forma de funcionamiento de la máquina de fabricación, en realidad la sección no estará completamente hueca, sino que tendrá un retículo de panal de abeja que servirá para sostener las capas superiores del material.
Modelo
El modelo fue preparado mediante el programa informático OpenSCAD, un programa de diseño asistido por computador en el que la descripción de los modelos se hace mediante texto en un lenguaje de programación especializado. OpenSCAD es software libre. Aquí están los modelos:
- Original de OpenSCAD.
- Modelo STL listo para convertir en un programa de fabricación con control numérico.
Puede ser necesario dividir el spinner en varias piezas si éste es demasiado grande para nuestra máquina de fabricación. Aquí hay una división en tres piezas:
- Modelo STL de la pieza trasera del modelo dividido en tres piezas.
- Modelo STL de la pieza central del modelo dividido en tres piezas.
- Modelo STL de la pieza delantera del modelo dividido en tres piezas.
El modelo también está disponible en Thingiverse, una página para compartir modelos de fabricación.
Dimensionado
Antes de lanzarnos a fabricar el spinner, tenemos que pararnos a echar unas pocas cuentas. Si no hacemos un dimensionado correcto, podemos acabar con una pieza tan flexible que se aplastará contra el suelo y no podrá girar bien o tan débil que se romperá bajo nuestro peso.
Vamos a usar el modelo de viga Euler-Bernoulli para estimar la respuesta del spinner como estructura. Este modelo es una simplificación de las ecuaciones generales de un sólido elástico que da buenos resultados para vigas esbeltas. El spinner no es una viga esbelta, así que podemos esperar errores notables y no parece conveniente apurar mucho en el diseño.
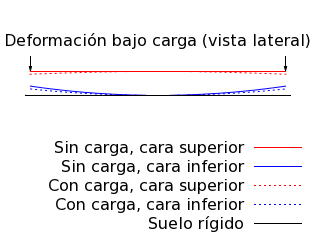
Representación esquemática de la flexión del spinner
bajo carga.
Supongamos que apoyamos nuestro peso W en los extremos anterior y posterior
del spinner. El contacto del rocker con el suelo es
puntual y está justo en el centro. Por equilibrio, la mitad de
nuestro peso se apoya en un extremo y la otra mitad en el otro.
El momento flector M es máximo
en la sección central y, si la longitud del spinner
es l (igual a la suma de los
parámetros back_length, middle_length y
front_length del modelo de OpenSCAD), su valor es
M = W l ⁄ 4.
Éste es el estado de carga más exigente.
Digamos que la altura de la sección extrema (el parámetro
platform_thickness del modelo de OpenSCAD) es H, el radio de curvatura del rocker
(el parámetro rocker_radius del modelo de OpenSCAD)
es R, el espesor de la pared de la sección hueca es t y la anchura de la sección es b. En un spinner general, la
sección no es de anchura constante, pero supondremos que sí para
hacer las cuentas y supondremos que esta anchura será igual a la del
parámetro rocker_width del modelo de OpenSCAD. La altura
h de la sección central es mayor que
la altura H de la sección extrema;
con buen nivel de aproximación para un spinner de proporciones
habituales, la altura es
h = H + l2 ⁄ (8 R).
El segundo momento I de área
de la sección con respecto del eje centroidal horizontal es
I = (1 ⁄ 12) [b h3 + (b − 2 t) (h − 2 t)3].
De acuerdo con el modelo de Euler-Bernoulli, la curvatura
de la línea directriz de la viga (es decir, del spinner)
se modifica en un valor
k = M ⁄ (E I).
La constante E es el módulo
de Young del material; supondremos que este valor es igual a 2,3 GPa para el ABS. Con esta propiedad
del material, el peso W, la longitud
l, la altura de la sección extrema
H, la anchura de la sección b, el radio del rocker R y el espesor de la pared de la sección
hueca t, podemos determinar el
cambio de curvatura por flexión k.
Para evitar que el rocker quede plano contra el suelo, este
cambio de curvatura ha de ser menor que la curvatura del rocker
R:
k < 1 ⁄ R.
Tras la flexión, el radio de curvatura del rocker crece hasta
el valor
1 ⁄ (1 ⁄ R − k),
así que tenemos que mantener dicho valor no muy alejado del adecuado
para girar bien (en torno a 1 m).
Las anteriores cuentas están hechas bajo la hipótesis de que el
material resiste la carga sin romperse. La resistencia del material
es S y puede estar en torno a los
35 MPa en el caso del ABS. Supondremos
que el material aguanta si la máxima tensión (que está en la fibra
superior de la sección central) se encuentra bien por debajo de este
valor de resistencia:
M h ⁄ (2 I) < S.
Veamos un ejemplo de aplicación de todo esto. Supongamos que la longitud es l = 260 mm, la altura de la sección extrema es H 15 mm, la anchura de la sección es b = 70 mm, el radio del rocker es R = 900 mm, el espesor de la pared de la sección hueca es t = 4,8 mm, el módulo elástico del material es E = 2,3 GPa, la resistencia es S = 35 GPa y queremos soportar un peso de 1000 N. Con estos números, el momento flector en la sección central es M = 65 N m, la altura de la sección central es h = 24,4 mm y el segundo momento de área de la sección central es I = 6,80 cm4. La curvatura debida a la flexión es 0,42 m−1, el radio de curvatura del rocker tras la flexión es de 1,4 m y la tensión máxima es de unos 12 MPa. Cumplimos los objetivos de evitar el aplastamiento del rocker contra el suelo y evitamos el fallo catastrófico del material con un factor de seguridad de 3.
Este modelo de diseño es muy grosero y tiene errores presumiblemente notables, pero ha sido validado al menos dentro de la gran incertidumbre de las medidas hechas a ojo tanto con un prototipo de pared muy delgada (cerca de 1 mm) como con el primer prototipo funcional (con una pared de 4,8 mm).
Fabricación
El spinner puede ser demasiado grande para la máquina de fabricación, pero es fácil hacerlo en varias piezas que luego pueden unirse. Con ABS, una buena técnica de unión consiste en la soldadura mediante disolvente: se añade una disolución viscosa de ABS en acetona o butanona en la interfaz y después se realiza la unión de las piezas; tras pasar unas horas, el disolvente se evapora y queda una soldadura muy decente para nuestros fines.

Pieza central del spinner hecho en tres piezas.
Se ve una hendidura en la parte superior cerca de la sección
central. Allí se producirá una delaminación. Esa zona es la
de tensión máxima según el modelo simplificado de flexión
presentado anteriormente. A la derecha, donde termina el
estrechamiento de la plataforma, hay una zona de concentración
de tensiones que también dará problemas.
Si, por motivos de facilidad de fabricación (para evitar distorsiones térmicas inaceptables, por ejemplo), hacemos el spinner capa a capa creciendo a lo largo de la dirección longitudinal, podemos tener problemas, ya que la cohesión entre láminas consecutivas del material puede ser un poco baja. Puede que se deslamine en la interfaz de dos secciones mal adheridas entre sí cerca del centro (donde el momento flector es máximo) o en la zona de concentración de tensiones que es el comienzo de la transición entre la anchura de la parte trasera y la anchura de la parte delantera. Es fácil mejorar la cohesión interlaminar cerca de la superficie frotando con un algodón empapado en acetona hasta uniformizar los surcos debidos al apilado de láminas y dejar una superficie lisa, continua y de elevada resistencia.
Resultados

El prototipo hecho en ABS. Hay franjas visibles que se deben
a las soldaduras de unión entre piezas y de reparación de las grietas
debidas a defectos de fabricación.
Preparé un prototipo en ABS. Está hecho en tres piezas creadas con una máquina de fabricación aditiva con láminas apiladas a lo largo de la dirección longitudinal (paralelas a la sección transversal). Las piezas están unidas mediante soldadura por fusión con acetona. Esta soldadura ha demostrado ser muy resistente tras secarse. También probé soldadura por fusión, pero la técnica era más trabajosa y las uniones resultantes salieron de calidad inferior a la de la soldadura por disolución debido a que sólo fue posible fundir un espesor muy pequeño.
La secuencia de apilado da malos resultados estructurales. La pieza se separó por deslaminado limpio dos veces: primero en el centro y después en donde la sección comienza a ensancharse. Ambos fallos fueron provocados aplicando cargas intensas de golpe para detectar puntos débiles. La unión de las piezas separadas ha resultado ser muy resistente y no volvió a fallar al estar completamente seca.
Froté las superficies con un trozo de algodón empapado en acetona hasta dejar un buen acabado. La superficie llena de surcos que resulta del apilado es débil comparada con una superficie uniforme y sólida. Hice el tratamiento después de provocar los dos fallos por deslaminación.
Gasté casi 300 g de material. Ésta no es la forma más económica de fabricar un spinner.
El spinner gira bien y no se aplasta contra el suelo. Una de las uniones quedó visiblemente desalineada, pero el efecto es de poca importancia a la hora de usar el aparato.

Spinner en acción visto de lado.
Permalink: https://sgcg.es/articulos/2012/05/27/skate-spinner/
Día de la Toalla
2012-05-25

El 25 de mayo es el Día de la Toalla, una fiesta en honor de Douglas Adams y de la propia toalla, la cosa más masivamente útil que puede uno tener.
Douglas Adams, aparte de hacer muchas otras cosas, escribió la
trilogía en cuatro partes (que gozó de una quinta entrega) The
Hitchhikker's Guide to the Galaxy (La Guía del Autoestopista
Galáctico). Ahora está tomándose la pausa para comer más larga
de la historia, así que lo menos que podemos hacer por el responsable
de tantas sonrisas es celebrar este día en su honor y, como siempre,
dedicarle unas palabras de agradecimiento: hasta pronto y gracias
por el pescado
.
Para celebrar el Día de la Toalla, hay que llevar encima una toalla durante todo el día. La toalla es extremadamente útil: podemos usarla toalla para cubrirnos del sol, plegada a modo de almohada, como látigo, para envolver un bocata, para taparnos los ojos si no queremos ver algo, atada a la cabeza como turbante, atada a la cintura como falda y, por supuesto, para secarnos.
Para terminar, recordemos estas palabras importantísimas:
¡QUE NO CUNDA EL PÁNICO!
Categorías: Fechas
Permalink: https://sgcg.es/articulos/2012/05/25/dia-de-la-toalla/
¿Puede romperse por su propio peso un cable tendido?
2012-05-21
Como continuación del artículo anterior sobre la curva catenaria que describen con buena aproximación cables, cuerdas, hilos y cadenas al colgar entre sus dos puntos extremos, veremos hoy en qué condiciones uno de estos elementos no podría sostener su propio peso y acabaría rompiéndose.
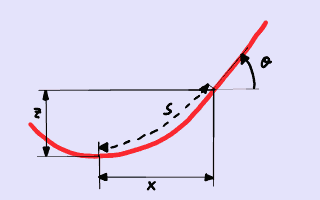
Sistema de coordenadas.
Recordemos la ecuación de la curva catenaria en coordenadas cartesianas. La coordenada horizontal es x, la coordenada vertical es z y la longitud de arco es s. Para concretar, fijamos el origen de coordenadas en el punto en el punto de mínima altura de la curva catenaria. El origen es sólo una referencia matemática y bien podría suceder que tal punto quedara fuera de la cuerda al acabarse ésta antes. Las ecuaciones son las siguientes:
z = [cosh(k x) − 1] ⁄ k,
s = |asinh(k x)| ⁄ k.

Geometría general de la catenaria.
La constante k está determinada por la geometría general: depende de la distancia vertical Δz entre los puntos extremos, la distancia horizontal Δx entre los puntos extremos y la longitud l de la cuerda. En concreto, vimos que el parámetro adimensional geométrico ξ ≡ k Δx ⁄ 2 y el parámetro adimensional dinámico η ≡ √[(l ⁄ Δx)2 − (Δz ⁄ Δx)2] tienen una relación funcional sencilla, de modo que si se conoce el parámetro η que sólo depende de la geometría, se deduce inmediatamente el parámetro ξ y, a partir de éste, el parámetro k:
η = sinh(ξ) ⁄ ξ.
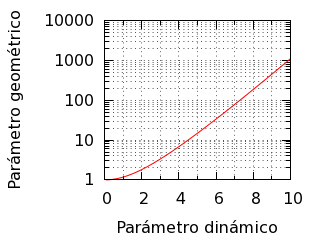
Parámetros adimensionales.
El parámetro adimensional geométrico η depende de las proporciones de las distancias horizontal Δx y vertical Δz entre los puntos extremos y la longitud l de la cuerda; si escalamos todo mientras mantenemos las proporciones (pasamos de los valores Δx, Δz y l a los valores c Δx, c Δz y c l), entonces el parámetro adimensional geométrico η se conserva inalterable, el parámetro adimensional dinámico ξ también se conserva inalterable y, finalmente el parámetro k de la curva escala como k = 2 ξ ⁄ Δx, es decir, es inversamente proporcional al tamaño de la cuerda para unas proporciones dadas.
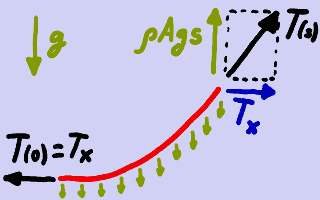
Equilibrio de fuerzas.
Vimos que la cuerda equilibra su peso mediante fuerzas internas de tracción. La fuerza de tracción T está dirigida según la dirección tangente a la cuerda y se extrae de los resultados del artículo anterior como
T = (ρ A g) √[(1 ⁄ k)2 + s2].
A la hora de analizar si se rompe o no la cuerda, lo interesante no es la fuerza resultante de tracción, sino la tensión σ = T ⁄ A. Vemos que la fuerza de tracción crece con la longitud de arco, así que será máxima en el extremo más alto, cuya longitud de arco smáx medida desde el origen de coordenadas es conocida. La tensión máxima σmáx es, por lo tanto, la siguiente:
σmáx = (ρ g) Δx √[1 ⁄ (2 ξ)2 + (smáx ⁄ Δx)2].
Hemos utilizado la relación entre el parámetro de la curva k y el parámetro adimensional dinámico ξ que sólo depende de las proporciones y no del tamaño absoluto.
Un buen modelo de resistencia de la cuerda consiste en que ésta se rompe cuando la tensión máxima σmáx supera cierto valor S que depende del material y de la construcción de la propia cuerda. Vemos que la tensión máxima es independiente del área A de la sección transversal, así que hacer que ésta crezca (con lo que aumenta el peso de la cuerda) no tiene efecto cuando es válido el modelo de cuerda inextensible a tracción y perfectamente flexible a flexión. Las otras maneras de aumentar el peso de la cuerda consisten en hacer crecer la densidad ρ (cambiar de material o construcción, pero esto probablemente cambiará la resistencia S), la aceleración gravitatoria g (¡irse muy lejos!) o hacer crecer el tamaño absoluto de la cuerda (representado aquí por la distancia horizontal Δx cubierta). El peso total aumenta linealmente con cualquiera de estas variables y la tensión máxima también aumenta linealmente con cualquiera de estas variables. Si nos limitamos a la geometría, vemos que, para unas proporciones «macroscópicas» (distancias a salvar y longitud de la cuerda) dadas, la cuerda puede romperse si se hace crecer mucho la dimensión absoluta «macroscópica», pero es insensible a la dimensión «microscópica» (el área de la sección transversal).
Categorías: Física, Matemáticas
Permalink: https://sgcg.es/articulos/2012/05/21/puede-romperse-por-su-propio-peso-un-cable-tendido/
El problema de la catenaria
2012-05-20

Curva catenaria descrita por una cadena colgante.
La catenaria es la curva que describe una cuerda inextensible a tracción, perfectamente flexible a flexión y de sección constante al colgar entre sus dos extremos sometida a su propio peso en un campo gravitatorio uniforme. Muchos objetos como hilos, cuerdas, cables y cadenas pueden ser descritos satisfactoriamente en muchas ocasiones mediante el modelo de la catenaria (cuyo nombre viene de «cadena»).
El problema de determinar la forma de la catenaria es un clásico de la mecánica aplicada. Veamos cómo resolverlo.

Sistema de coordenadas del problema.
Definamos algunas propiedades para nuestra cuerda. La densidad del material es ρ, el área de la sección transversal es A, la aceleración gravitatoria es ρ, la longitud de arco a lo largo de la cuerda es s, la coordenada horizontal a lo largo de la cuerda es x, la coordenada vertical a lo largo de la cuerda es z, el ángulo que forma con la horizontal un segmento elemental de cuerda es θ y la fuerza de tracción en una sección transversal de cuerda es T.

Equilibrio de fuerzas.
En el equilibrio, la cuerda mantiene su forma. El peso queda equilibrado por la fuerza de tracción. Como la fuerza de gravedad va según la vertical, la proyección vertical de la fuerza de tracción depende del peso que sostiene debajo de sí cada punto de la cuerda, pero la proyección horizontal es constante. Si llamamos Tx a dicha proyección horizontal, nos queda la siguiente igualdad:
T cos(θ) = Tx.
En cuanto a la proyección vertical, ésta adopta la siguiente forma si tomamos como origen de arcos s = 0 el punto más bajo de la cuerda:
T sin(θ) = ρ A g s.
La tangente del ángulo θ que forma con la horizontal un segmento elemental de cuerda es, por lo tanto,
dz ⁄ dx = tan(θ) = sin(θ) ⁄ cos(θ) = (ρ A g ⁄ Tx) s = k s.
Introducimos la constante k para aligerar la notación.
Unas nociones elementales de geometría diferencial nos dicen que el elemento diferencial de longitud de arco ds es el siguiente:
ds = √(1 + dz ⁄ dx) dx.
Estas dos últimas ecuaciones junto con una condición inicial adecuada (digamos x = 0 en el origen de arcos s = 0) son suficientes para relacionar la coordenada horizontal con la longitud de arco. En efecto queda una ecuación cuya integral es inmediata:
ds ⁄ dx = √(1 + k2 s2)
⇒ k s = |sinh(k x)|.
El valor absoluto se toma para que la longitud de arco sea siempre positiva.
Si introducimos el último resultado en la ecuación de la pendiente e integramos con la condición inicial y = 0 para x = 0, queda el siguiente resultado, la forma explícita de la curva catenaria:
z = [cosh(k x) − 1] ⁄ k.
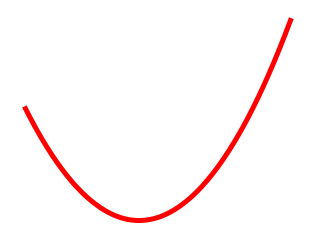
Curva catenaria.
La constante k es muy molesta, pero podemos determinarla fácilmente si conocemos la longitud l de la cuerda, la distancia vertical Δz entre los extremos y la distancia horizontal Δx entre los extremos. De las ecuaciones que relacionan la posición vertical z y la longitud de arco s con la posición horizontal x, tras un poco de álgebra, sale lo siguiente:
[l2 − (Δz)2] k2 = 4 [sinh(k Δx ⁄ 2)]2.

Geometría general del problema.
Si introducimos el parámetro dinámico ξ ≡ k Δx ⁄ 2 y el parámetro geométrico η ≡ √[(l ⁄ Δx)2 − (Δz ⁄ Δx)2], queda una función uniparamétrica muy conveniente que podemos pintar una sola vez para calcular gráficamente el parámetro de la catenaria:
η = sinh(ξ) ⁄ ξ.

Parámetros de la catenaria. El parámetro dinámico es la
variable ξ de la anterior
ecuación y el parámetro geométrico es la variable η de la anterior ecuación.
Categorías: Física, Matemáticas
Permalink: https://sgcg.es/articulos/2012/05/20/el-problema-de-la-catenaria/
Día de Hablar como un Piloto
2012-05-19
El 19 de mayo es el Día de Hablar como un Piloto. Hay que usar jerga de piloto de aviación. Idealmente, hay que hablar como los antiguos pilotos de caza británicos y estadounidenses. He aquí una pequeña muestra de vocabulario para defenderse:
- Angels:
- La altitud medida en miles de pies.
- Bandits:
- Los aviones enemigos hostiles.
- Bingo:
- Se dice cuando se ha bajado de cierto nivel de reserva de combustible. Por ejemplo, se está bingo cuando ya no queda combustible para regresar a base.
- No joy:
- Lo opuesto a «tally ho».
- Roger:
- Sirve para decir que uno ha entendido un mensaje.
- Tally ho:
- Enenigo avistado.
- Wilco:
- Sirve para decir que uno ha entendido una orden y va a cumplirla. Viene de «will comply».
- Winchester:
- Ya no queda armamento.
- Wingman:
- Nuestro punto, es decir, el piloto que vuela en nuestro avión acompañante y vigila nuestras seis.
Podemos dar las direcciones como los números de la esfera de un reloj: nuestras doce están delante, nuestras seis están detrás, nuestras tres están a la derecha y nuestras nueve están a la izquierda.
Finalmente, viene bien recordar el alfabeto fonético.
Categorías: Aeroespacio, Fechas
Permalink: https://sgcg.es/articulos/2012/05/19/dia-de-hablar-como-un-piloto/
Gatito bufando
2012-05-15
Hoy parece ser un día excelente para dibujar gatitos, así que aquí tenéis uno:

Imagen PNG en paleta de 256 colores, 800 píxeles de ancho y 500
píxeles de alto, 101,3 kB.
Categorías: Dibujos
Permalink: https://sgcg.es/articulos/2012/05/15/gatito-bufando/
Fotografías de la manifestación del 12M (12 de mayo de 2012) en Madrid
2012-05-12
El 12 de mayo de 2012, casi al hacer un año desde las manifestaciones por una democracia real que tuvieron lugar a lo largo y ancho de España el 15 de mayo de 2011, hubo nuevas movilizaciones con similares motivos en muchos lugares distribuidos por todo el mundo. Este artículo recoge imágenes captadas en la manifestación de Madrid. Esta manifestación, a la que acudieron varias decenas de miles de personas, partió de varios frentes y acabó en Sol.

Grandes figuras con forma de chorizo. Juega con el significado
de «chorizo» como 'ladrón'.

Cartel. Dice así: El emperador está desnudo
. Es una
referencia al famoso cuento El traje nuevo del emperador.
Indica que el dirigente actúa engañado de forma contraproducente,
pero nadie alrededor de él se atreve a señalar la bochornosa y
evidente realidad.

Cartel. Dice así: Un pueblo inculto es un pueblo manejable
.

Una máscara de Guy Fawkes cuelga tras la cabeza de un hombre.

Cartel. Dice así: Llevamos un mundo nuevo en los corazones y lo estamos sacando
.

Cartel. Dice así: La calle es de todos
.

Cartel. Dice así: Cambia la palabra 'crisis' por
'estafa'; verás cómo las cuentas te cuardan
.

Cartel. Dice así: No somos antisistema; el sistema está en contra
de nosotros
.

Figura con forma de bastoncillo descomunal de los que a menudo
son usados para despejar los canales auditivos. Tiene un cartel en
el que pone lo siguiente: Usar en caso de sordera política
.

Cartel muy florido. Dice así: Podrán cortar todas las flores,
pero no detendrán la primavera
.

Cartel. Dice así: Pon tu mente al sol
.

Cartel. Dice así: Paremos su sueño
. Hay un diagrama con
forma triangular (o lo que se conoce como «piramidal»); en la cima,
en representación de una mínima parte de la población, pone ricos
;
en la base, en representación de la mayor parte de la población, pone
pobres esclavos
.

Cartel elaborado con un trozo de tela (quizá una sábana) y colgado
de un balcón por una vecina. Dice así: Dormíamos, despertamos. Toma
la plaza
.

Cartel. Dice así: Disculpe las molestias; estamos cambiando
el mundo para usted. Muchas gracias
.

Cartel. Dice así: La próxima vez voto a Alí Babá; así sé que
sólo me robarán 40 ladrones
. Debajo: Hace un año que salió
el sol
.

Cartel. Dice así: Mi madre luchó para que fuese una mujer
libre; mi padre, para que fuese una estudiante con derechos. Yo
lucho por un trabajo digno para ellos
.

Manos arriba en Carretas. Entrar en Sol es una labor complicada
debido a la gran afluencia de gente.

Sol repleta de gente.

Sol abarrotada.
Categorías: Actualidad, Derechos, Madrid
El caso de Oracle contra Google y el copyright de las interfaces de programación
2012-05-08
Los litigios entre grandes compañías de informática y
telecomunicaciones son alarmantemente frecuentes. Se encuentran
favorecidos por mecanismos de creación de monopolios artificiales
como el copyright y las patentes, muy utilizados en estas
industrias. Dos gigantes que se encuentran en contienda son Oracle
y Google. Google está acusada de violar algunos privilegios
monopolísticos de Oracle en el desarrollo del sistema Android que
se usa en teléfonos móviles y dispositivos similares. Una de
las acusaciones que está dando mucho de lo que hablar es la de
que Google habría violado el copyright de la interfaz de
programación del lenguaje Java. Este concepto es algo inverosímil:
la posibilidad de imponer un monopolio de copyright sobre la
estructura, la secuencia y la organización (structure, sequence
and organisation o SSO en inglés) del código que
implementa una interfaz de programación. Es decir, no se trata de
cubrir copias literales, sino de cubrir cómo se organiza en general
el código informático que cumple con una determinada interfaz de
programación. Por eso se habla del copyright sobre una
API (interfaz de programación)
. Recientemente, el jurado se ha
pronunciado sobre esta acusación… pero bajo el supuesto de que
la cuestión del monopolio de copyright sobre una interfaz de
programación tuviera fundamento. La cobertura dada en muchos sitios
es mala, así que lo mejor será dar un enlace a las impresiones recogidas
ayer en Groklaw.
En resumen, la situación que mueve más los ánimos (¡pero las acusaciones son más complejas!) es ésta:
- Está la acusación de haber violado el monopolio del copyright sobre una interfaz de programación.
- El juez instruye al jurado para que decida si, en el caso hipotético de que tal violación fuera posible, tal violación se habría dado.
- El jurado decide que la compañía acusada copió la interfaz de programación, así que, si ésta estuviera bajo monopolio de copyright, entonces tal monopolio habría sido violado.
- Ahora el juez ha de decidir si un monopolio de copyright sobre una interfaz de programación es posible.
Esto es muy importante. El jurado no ha llegado a la conclusión de que Google ha violado el copyright de Oracle porque tal copyright se encuentra en un limbo legal. El jurado ha decidido que, si tal copyright existiera, entonces se habría producido la violación. Ésta es la decisión sobre materia fáctica que ha de tomar el jurado. Ahora, es el juez el que ha de tomar la decisión sobre la materia legal: ¿es el monopolio del copyright aplicable a este caso? De haber sido diferente la conclusión del jurado, no habría ahora necesidad de tomar la decisión sobre materia legal.
Estructura, secuencia y organización
Se habla de la existencia o no de monopolio de
copyright sobre la estructura, la secuencia y la
organización del código informático que implementa
una interfaz de programación. Este concepto cubre no
la realización literal del código, sino su forma general.
Tomemos como analogía un libro. Esta analogía está sacada de una
contribución a la discusión en Groklaw por parte del usuario
calris74. Aquí se habla no de cubrir con un monopolio la
secuencia explícita de palabras del contenido del libro, sino su
índice, su secuencia de capítulos y el concepto general de cada
capítulo (pero no necesariamente el texto que aparece literalmente en
cada capítulo). Esto viene a ser lo mismo que cubrir no la interfaz
de programación (que se considera una colección de hechos y, por lo
tanto, materia no sujeta a copyright), pero sí cualquier uso de
ésta, de modo que la propia interfaz queda cubierta no de jure,
pero sí de facto, ya que su función, que es ser implementada,
queda restringida. Así que si alguien pregunta si realmente se trata
de monopolizar mediante copyright una interfaz de programación
(una API), la respuesta es no, pero sí
.
El copyright y las interfaces de programación
Todo esto nos lleva al centro del asunto: la posibilidad de imponer un monopolio de copyright sobre la estructura, la secuencia y la organización del código informático que implementa una interfaz de programación, esto es, sobre cómo están organizados los paquetes, la secuencia de métodos y sus signaturas… Se monta mucho revuelo porque se plantea algo inverosímil: es como si se acusara a un tipo en silla de ruedas de no tener luces de freno en su silla… ¡pero la obligación de llevar luces de freno es para automóviles, no para sillas de ruedas!
¿Por qué es este caso importante?
Peleas entre gigantes las hay todos los días. El sistema fomenta efectivamente estos litigios improductivos. Si uno no tiene un interés económico especial en una de las partes implicadas, puede parecer que el caso es irrelevante, pero lo malo del asunto es que tiene un alcance potencialmente inmenso. Si el juez determina que la estructura, la secuencia y la organización del código que implementa una interfaz de programación es materia sujeta a copyright, entonces se abre la puerta a una hostilidad expansionista similar a la desatada en las últimas décadas en Estados Unidos con motivo de las patentes de software y modelos de negocio, pero con una capacidad aumentada para traspasar fronteras. La experiencia sugiere más batallas en los tribunales, más herramientas para eliminar toda competencia del mercado y más herramientas para el enriquecimiento sin producir trabajo útil.
Actualización: el juez que lleva el caso se ha pronunciado sobre este asunto.
Categorías: Actualidad, Informática
Setenta y cinco aniversario del desastre del Hindenburg
2012-05-06
Tal día como hoy, el 6 de mayo de 1937, ocurrió uno de los accidentes más trágicamente famosos de la historia de la aeronáutica: el desastre del Hindenburg.
El LZ 129 Hindenburg era, aparentemente, una joya de la ingeniería. Con sus 245 m de longitud y la capacidad de transportar 72 pasajeros y 62 tripulantes en una lujosa cabina a un máximo de unos 38 m ⁄ s (esto es ciento treinta y cinco kilómetros por hora) y con un crucero de unos 35 m ⁄ s (esto es ciento veinticinco kilómetros por hora) entre Europa y América a través del Atlántico, este enorme dirigible era una fuente de gran orgullo para la Alemania nazi. Voló durante los años 1936 y 1937 y no tuvo parangón más allá del LZ 130 Graf Zeppelin II, el segundo dirigible de la clase Hindenburg, completado más adelante y que no llegó a realizar operaciones comerciales de transporte de pasajeros.
El 6 de mayo de 1937, el imponente LZ 129 Hinenburg se preparaba para amarrarse en tierra estadounidense en la Estación Aeronaval de Lakehurst (Manchester, Nueva Jersey), pero la maniobra se vio tristemente interrumpida por un fuego que se extendió rápidamente a lo largo del dirigible. En esos momentos, había sesenta y un tripulantes y treinta y seis pasajeros. El accidente acabó con la vida de veintidós tripulantes y trece pasajeros. Estos lamentables hechos fueron cubiertos por los medios de comunicación y la noticia del desastre dio la vuelta al mundo.
La causa del accidente que acabó con el Hindenburg es objeto de cierta controversia. He aquí una explicación muy popular: el revestimiento, realizado con materiales dieléctricos y altamente inflamables, se incendió como consecuencia de una chispa provocada por la carga que naturalmente acumulaba. Fuera cual fuera el mecanismo de la ignición, se entiende que el fuego se extendió rápidamente por el revestimiento y que el fluido sustentador, hidrógeno, ardió fácilmente al entrar en contacto con el oxígeno atmosférico y las llamas del revestimiento.
En buena medida, el desastre del Hindenburg es la marca psicológica del final de la era de los dirigibles como medio de transporte de pasajeros. A la imagen de inseguridad hay que añadir la competencia del avión, quizá menos cómodo pero mucho más rápido.
Categorías: Aeroespacio, Historia
Permalink: https://sgcg.es/articulos/2012/05/06/setenta-y-cinco-aniversario-del-desastre-del-hindenburg/
Día sin Pantalones
2012-05-04
El primer viernes de mayo es el Día sin Pantalones. ¿Qué hay que hacer? ¡No llevar pantalones! Las prendas sustitutivas del pantalón tales como las faldas también están descartadas.
Categorías: Fechas
Permalink: https://sgcg.es/articulos/2012/05/04/dia-sin-pantalones/
