Enero de 2016
Calendario de artículos de de 2016
| lu | ma | mi | ju | vi | sá | do |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Campeonato de Europa de Patinaje Artístico sobre Hielo de 2016 (4)
2016-01-30
Esta semana se ha celebrado el Campeonato de Europa de Patinaje Artístico sobre Hielo de 2016 en Bratislava. España participa en las cuatro categorías: individual femenino con Sonia Lafuente; individual masculino con Javier Fernández y Felipe Montoya; danza con Celia Robledo y Luis Fenero; y parejas con Marcelina Lech y Aritz Maestu. Hoy ha terminado la competición con los largos de parejas y danza.
- En parejas, Marcelina Lech y Aritz Maestu han cometido algunos errores muy caros y han descendio al puesto 15. Son cosas que pasan. El primer puesto ha ido a la pareja rusa formada por Tatiana Voloshozar y Maxim Trankov, que ha mantenido unos formidables veintitantos puntos de distancia por encima de los siguientes: los alemanes Aliona Savchenko y Bruno Massot, que han quedado a una relativamente corta distancia por encima de los terceros, Evgenia Tarasova y Vladimir Morozov, quienes han competido por Rusia.
- En danza, Celia Robledo y Luis Fenero han estado muy bien con un único error reseñable: la primera elevación se pasó de tiempo alguna décima de segundo. Acaban en el puesto número 19. La primera posición es para los franceses Gabriella Papadakis y Guillaume Cizeron, siempre excelentes, que se han llevado un oro que ya acariciaban los italianos Anna Cappellini y Luca Lanotte. La pareja rusa formada por Ekaterina Bobrova y Dmitri Soloviev, tercera, ha estado a punto de robarle el siguiente metal a los italianos.
Categorías: Actualidad, Deporte
Campeonato de Europa de Patinaje Artístico sobre Hielo de 2016 (3)
2016-01-29
Esta semana se celebra el Campeonato de Europa de Patinaje Artístico sobre Hielo de 2016 en Bratislava. España participa en las cuatro categorías: individual femenino con Sonia Lafuente; individual masculino con Javier Fernández y Felipe Montoya; danza con Celia Robledo y Luis Fenero; y parejas con Marcelina Lech y Aritz Maestu. Hoy han tenido lugar los cortos de parejas y los largos de la categoría individual femenina.
- En parejas, Marcelina Lech y Aritz Maestu han estado bien, aunque no limpios. Se trata del segundo Europeo de Aritz y el primero con Marcelina, su pareja desde el año antepasado. El primer puesto lo tiene, por el momento y como dictan las leyes de la naturaleza, la pareja rusa formada por Tatiana Voloshozar y Maxim Trankov. En el segundo puesto están los alemanes Aliona Savchenko y Bruno Massot, quienes estrenan Europeo juntos francamente bien. El tercer puesto va por el momento para otra pareja rusa: la formada por Evgenia Tarasova y Vladimir Morozov. Sería muy sorprendente que estos tres primeros puestos cambiaran tras el largo.
- En la categoría individual femenina, la armada moscovita asienta los resultados obtenidos en el corto: Evgenia Medvedeva queda primera, Elena Radionova queda segunda y Anna Pogorilaya queda tercera. Salía una quiniela fácil.
Mañana tocan los largos de parejas y danza.
Categorías: Actualidad, Deporte
Campeonato de Europa de Patinaje Artístico sobre Hielo de 2016 (2)
2016-01-28
Esta semana se celebra el Campeonato de Europa de Patinaje Artístico sobre Hielo de 2016 en Bratislava. España participa en las cuatro categorías: individual femenino con Sonia Lafuente; individual masculino con Javier Fernández y Felipe Montoya; danza con Celia Robledo y Luis Fenero; y parejas con Marcelina Lech y Aritz Maestu. Hoy han tenido lugar los cortos de danza y los largos de la categoría individual masculina.
- En danza, Celia Robledo y Luis Fenero han hecho un trabajo mucho mejor que el año pasado y, de hecho, han presentado su mejor programa corto. El primer puesto temporal lo tienen los italianos Anna Cappellini y Luca Lanotte con un muy buen programa. Les siguen los franceses Gabriella Papadakis y Guillaume Cizeron y los rusos Ekaterina Bobrova y Dmitri Soloviev.
- En la categoría inidividual masculina, súper Javier Fernández ha quedado más que primero, único. Incluso con algunos fallos, ha dejado 60 puntos (¡un abismo!) de distancia hasta el segundo puesto de Alexei Bychenko y el tercero de Maxim Kovtun. ¡Esto es ensañamiento! Michal Brezina se estrelló hasta acabar décimo, mientras que los dos mejores largos en la categoría «no-Javier-Fernández» fueron el de Florent Amodio (octavo mejor corto) y el de Mikhail Kolyada. Felipe Montoya presentó un largo quizá algo sucio, pero digno en general y bueno para un estreno en el Campeonato de Europa.
Mañana tocan los cortos de parejas y los largos de la categoría individual femenina.
Categorías: Actualidad, Deporte
Campeonato de Europa de Patinaje Artístico sobre Hielo de 2016 (1)
2016-01-28
Esta semana se celebra el Campeonato de Europa de Patinaje Artístico sobre Hielo de 2016 en Bratislava. España participa en las cuatro categorías: individual femenino con Sonia Lafuente; individual masculino con Javier Fernández y Felipe Montoya; danza con Celia Robledo y Luis Fenero; y parejas con Marcelina Lech y Aritz Maestu. Ayer tuvieron lugar los cortos femeninos y masculinos.
- En la categoría individual femenina, Sonia Lafuente estuvo flojilla y acabó en el puesto 33, lo que la deja fuera de la final. Los tres primeros puestos los tiene por ahora la artillería rusa: Evgenia Medvedeva, Elena Radionova y Anna Pogorilaya.
- En la categoría inidividual masculina, súper Javier Fernández ha vuelto a construirse su propia categoría con la friolera de 102,54 puntos. Se trata de la segunda mejor puntuación en un corto de la historia, solamente superada por 110,95 puntos del amiguete Yuzuru Hanyu en la la final del último Grand Prix. La combinación inicial fue ligeramente sucia, pero luego pasó todo rápidamente al terreno de los libros de texto. A una distancia que provoca mareo están el ruso Maxim Kovtun y un checo Michal Brezina que apenas tiene margen de seguridad por encima de Alexei Bychenko, que patina por Israel. El debut en un Europeo de Felipe Montoya ha sido excelente: ha alcanzado el puesto número 17 con un programa casi limpio.
Hoy sigue la competición con los programas cortos de danza y los largos de la categoría individual masculina.
Categorías: Actualidad, Deporte
Tolerancias y juegos
2016-01-25
Los juegos y las tolerancias son magnitudes que tienen que ver con las dimensiones de ingenios (quizá muebles, quizá máquinas…) que diseñamos y fabricamos. Aunque las tolerancias y los juegos están relacionados, son conceptos diferentes.
- Las tolerancias son una especificación sobre lo que es admisible al fabricar una pieza. La tolerancia de una medida es lo que estamos dispuestos a admitir que se desvíe de su valor de básico de diseño. Si una dimensión se sale del intervalo de tolerancia, consideramos que está mal hecha. Habría que elegir las tolerancias de manera que su satisfacción implique que las piezas funcionan. De hecho, podemos considerar que no hay un valor de diseño con una tolerancia, sino un intervalo de valores que podemos aceptar, de manera que si las piezas fabricadas entran dentro de la zona de tolerancia, tenemos cierta garantía de que van a funcionar como queremos (que un eje encaja dentro de un agujero, por ejemplo).
- Los juegos son espacio libre: diferencias entre dos dimensiones. Si un tornillo tiene un diámetro de 3 mm y un agujero por el que tiene que pasar tiene un diámetro de 4 mm, entonces hay un juego diametral de 1 mm, que es lo que va del diámetro del tornillo al diámetro del agujero. Igual que los juegos son espacio libre, existen las interferencias geométricas, que son juegos negativos: se dan cuando unas piezas tienden a ocupar el espacio de otras. Si tenemos un eje más grande que el agujero por el que tiene que pasar, decimos que hay interferencia geométrica.
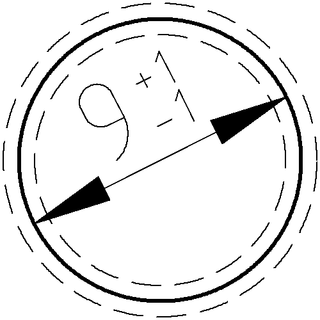
Concepto de tolerancia: esta pieza redonda (línea gruesa) tiene un
diámetro básico de diseño de 9 mm, pero
sería aceptable hacerla con un diámetro
entre 8 mm
y 10 mm (líneas de trazos)
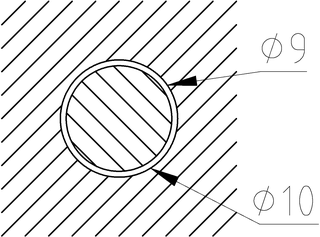
Concepto de juego: la pieza central tiene un diámetro
de 9 mm y cabe dentro de un agujero de
10 mm. El juego, que es
de 1 mm diametral, es el espacio que
hay entremedias, lo que podría crecer el diámetro de la pieza interior
o lo que podría encoger el diámetro del agujero sin impedir que la
pieza interior cupiera en su sitio.
Los juegos y las tolerancias pueden condicionarse entre sí. Puede darse el caso, por ejemplo, de que busquemos que una pieza quepa dentro de otra: si tenemos un hueco que como mínimo medirá 100 mm y tenemos que hacer una pieza cuya dimensión básica de diseño es de 99 mm (con lo que el juego básico de diseño es de 1 mm, podemos permitirnos (¡tolerar!) fabricar esta pieza con un tamaño de hasta 100 mm sin que ello impida el montaje (sin que haya interferencia geométrica). Si todavía no hemos asignado tolerancias, pero ya tenemos las dimensiones básicas de diseño asignadas, podemos repartir las amplitudes de los juegos básicos de diseño entre las tolerancias de las distintas piezas para garantizar que los juegos fabricados sean siempre suficientes para permitir que los conjuntos funcionen.
De vuelta a las tolerancias, hay que decir que son un concepto inherente al diseño de una pieza, no a la maquinaria y los procesos para fabricarla: la tolerancia es la desviación aceptable de la geometría básica de diseño, no la capacidad de una máquina herramienta. Aun así, por abuso del lenguaje se habla a menudo de la tolerancia que tiene un proceso productivo o una máquina herramienta; realmente lo que habría que indicar es la tolerancia que el proceso o la máquina puede satisfacer. De igual manera, las piezas no salen fabricadas con una tolerancia, sino con cierta precisión y cierta exactitud.
Por una parte, las tolerancias son un reconocimiento de que no podemos esperar fabricar piezas con la geometría exacta del diseño; al no poder hacerlo, tenemos que preguntarnos cuánto podemos desviarnos sin que las piezas dejen de servirnos. Por otra parte, las tolerancias son un reconocimiento de que nuestro diseño no es realmente una geometría única, sino el conjunto de todas las que permiten el funcionamiento que deseamos.
Categorías: Miscelánea
Permalink: https://sgcg.es/articulos/2016/01/25/tolerancias-y-juegos/
Botones de madera
2016-01-22
Me dio por hacer botones en madera de cerezo para ponerlos en bolsitos. Me gusta el aspecto que tienen. Los hago de cerca de 25 mm de diámetro (un poco menos) y unos 4 mm o 5 mm de espesor. El trabajo es fácil de hacer en torno para madera y fresadora vertical (o taladro de columna).

Botones de madera.
Quizá el detalle más peculiar de estos botones es que están torneados con la fibra en vez de según el eje de giro (que sería lo normal), perpendicular al eje de giro (contenida en el plano del botón). Los hice así porque conseguía un aspecto bajo la luz de la veta de la madera en las caras de los botones que me gustaba especialmente. La desventaja de esta forma de trabajar es que se desperdicia mucho material, ya que la pieza más alargada de la que es posible partir es bastante corta (un cubo) y el trozo que hay que reservar para hacer la sujeción ocupa una parte importante de la longitud total. Con esta técnica tan poco eficiente, de un cubo de madera me salen dos o quizá tres botones.

Cubo de madera sujeto en el torno.
El trabajo en torno es muy sencillo. Tras cilindrar el tarugo inicial al diámetro buscado, hago la cara frontal con una herramienta raspadora (con la que doy una forma general) y una gubia fina (con la que acanalo).

Cara terminada.
Después, hago una ranura profunda hasta casi tronzar la pieza del todo (queda un cuello de unos pocos milímetros de diámetro) y dejar el botón con un espesor que me agrada. Seguidamente, lijo hasta grano 400 por el canto y las dos caras.

Lijado en el torno.
Finalmente, termino de separar el botón.

Pieza tronzada.
La pieza sale bien lijada salvo por el resto del cuello que queda al tronzar. Acabo el trabajo en una fresadora vertical, aunque valdría igualmente un taladro de columna. Primero, sujeto la pieza a un plato de garras y hago cuatro taladros espaciados entre sí un cuarto de vuelta. Uso una broca de 1,5 mm para poder coser cómodamente.

Taladrado.
Para eliminar el resto del cuello, volteo la pieza y ataco cuidadosamente con un plato de lija.

Lijado en el torno.
Con esto, ya está hecho un botón. Luego es posible darles un acabado adaptado a su uso. Los últimos que hice están acabados con aceite danés.

Botones de madera acabados.
Categorías: DIY
Permalink: https://sgcg.es/articulos/2016/01/22/botones-de-madera/
El agujero analógico
2016-01-18
Son numerosísimas las obras literarias y audiovisuales que se distribuyen de forma digital. Los sistemas digitales posibilitan, en principio, la copia fidedigna, la distribución y la reproducción de las obras con un coste minúsculo. Para mantener un control estricto sobre la copia y la reproducción de las obras en formato digital, muchas empresas plantean sistemas que restringen lo que pueden hacer los consumidores. En el momento que un aparato reproductor de obras digitales implementa estos sistemas digitales de restricciones, este aparato deja de servir a su dueño (o quizá lo que sucede es que este dueño no es quien compró el aparato, sino la empresa que está detrás de él): podemos decir que es defectuoso por diseño. Ahora bien, a día de hoy y mientras no se descargue el contenido directamente en la mente del consumidor, la reproducción de obras en formato digital siempre tiene un lado analógico: la información tiene que manifestarse físicamente de manera que sea perceptible por los sentidos de la persona que va a disfrutar de ella. Incluso si toda la cadena de transmisión de una obra digital desde su origen hasta el aparato reproductor está bajo el control férreo de la empresa que pone las restricciones, el eslabón final, analógico, es un agujero difícil de tapar: por una parte, muchos aparatos reproductores aceptan una señal analógica modulada para su reproducción inmediata; por otra parte, si un ser humano puede percibir la obra con sus sentidos, entonces un aparato de grabación puede registrar la información física perceptible y copiarla. Esto es lo que se conoce como agujero analógico (término usado desde al menos la década pasada). Habitualmente, el concepto de agujero analógico suele referirse a las salidas analógicas que van a televisores y altavoces, pero también se usa (aunque con menos frecuencia) para lo que puede considerarse como el agujero analógico definitivo: las señales acústicas y luminosas que interpretan los sentidos humanos.
El agujero analógico es amplio y difícil de tapar, pero no imposible de tapar: por una parte, los nuevos aparatos reproductores tienen a menudo menos salidas analógicas que antes; por otra parte, no es inconcebible que en un futuro todos los medios de grabación y reproducción acaben bajo el control de unas pocas empresas que implementen sistemáticamente mecanismos automatizados que permitan bien impedir la grabación (mediante la emisión de una señal de control que bloquee los aparatos de grabación, por ejemplo), bien impedir la reproducción (mediante sistemas automatizados de identificación de contenidos, por ejemplo). A lo largo de la última década, han sido varios los intentos por parte de grupos de presión para forzar la introducción de leyes que hicieran obligatorias algunas medidas para tapar el agujero analógico, así que el asunto no es para tomárselo a broma.
Categorías: Miscelánea
Permalink: https://sgcg.es/articulos/2016/01/18/el-agujero-analogico/
La Wikipedia cumple tres lustros
2016-01-15
Wikipedia cumple 15 años. Tal día como hoy, el 15 de enero de 2001, Jimmy Wales y Larry Sanger lanzaban al público Wikipedia, la enciclopedia libre, un recopilatorio del saber humano que todo el mundo está invitado a usar y a construir. Es un hecho notabilísimo. En estos quince años, la Wikipedia ha prosperado espectacularmente. Esperemos que los próximos quince sean igual de buenos o mejores.
Categorías: Actualidad
Permalink: https://sgcg.es/articulos/2016/01/15/la-wikipedia-cumple-tres-lustros/
Ventajas de tener un torno paralelo: adaptar canillas
2016-01-14
Tengo un tornito paralelo miniatura y estoy encantado con él. También tengo canillas cuyo agujero es demasiado estrecho para el eje del devanador de mi máquina de coser. Me resulta especialmente fácil conseguir estas canillas, pero tengo que adaptarlas si quiero bobinarlas con el devanador motorizado. Esto es fácil de hacer con el torno paralelo: basta usar una cuchilla de mandrinar pequeña (¡de 3 mm!) para ampliar el agujero hasta que encaje con el apriete justo en el eje del devanador. El diámetro es fácil de encontrar si se usa una canilla de diámetro correcto como referencia: con esta canilla bien sujeta y centrada en el torno, se busca la superficie del agujero con la cuchilla. Aunque las canillas de plástico son a menudo visiblemente irregulares, sale un centrado muy decente en el plato de garras sin más que presionar la canilla contra el fondo del plato y apretar las garras bien sin miedo a deformar un poco las alas hasta que queden completamente sujetas.

Corrigiendo una canilla en el torno.
Las canillas así corregidas funcionan maravillosamente.
Categorías: DIY
Permalink: https://sgcg.es/articulos/2016/01/14/ventajas-de-tener-un-torno-paralelo-adaptar-canillas/
Peoncita de latón (2)
2016-01-12
Hace unos meses, hice una pequeña peonza de latón en mi tornito paralelo miniatura. Estaba hecha con un contorno de líneas rectas (cilindros y conos) y tenía ganas de hacer una con una forma más redondeada. Por fin fabriqué una así.

Peoncita girando.
Esta peonza tiene una longitud de 3 cm y un diámetro máximo de 15 mm. Está hecha en torno de operación manual siguiendo un diseño dibujado en papel cuadriculado con una escala tal que cada cuadro tiene un lado correspondiente a 0,5 mm en la realidad.
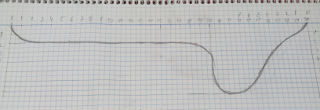
Diseño en papel cuadriculado.
Para hacer la peonza en el torno, cilindré en escalones de 0,5 mm de acuerdo con la aproximación del contorno curvilíneo a la cuadrícula, siempre con cuchilla de cortar hacia la izquierda, primero del lado del mango y, después, tras voltear, del lado de la punta. La cosa quedaba así:

Torneado escalonado.
Después de esto, suavicé el contorno con papel de lija hasta llegar al grano 400. El resultado fue razonablemente similar al diseño:

Tras el lijado.
La peonza es muy pequeña, pero no gira del todo mal.

Otra fotografía de la peonza en pleno giro.
Categorías: DIY
Permalink: https://sgcg.es/articulos/2016/01/12/peoncita-de-laton-2/
La primera es gratis o el empinado plan de precios de la naturaleza
2016-01-11
Es admirable lo mucho que puede comprenderse sobre la naturaleza con una pequeña inversión de tiempo y recursos intelectuales. Asombrados ante nuestra propia audacia y capacidad de predecir el comportamiento del mundo, usamos nuestros conocimientos para diseñar y construir máquinas de creciente sofisticación. Al principio, la naturaleza es generosa con nosotros y se deja modelar (y, con ello, moldear) con gran facilidad. Sin embargo, cuando queremos dar un paso más allá, cuando queremos crear una máquina ligeramente más capaz y eficiente o indagar en misterios más profundos, la naturaleza se rebela ante nosotros y nos exige un coste (de sofisticación matemática, de capacidad de cómputo, de habilidad constructiva) que se hace rápidamente abrumador. Es como si la naturaleza nos ofreciera a probar lo que se siente al ser un dios y, tras engancharnos como a una droga, nos exprimiera cruelmente.
Son numerosísimos los fenómenos que podemos modelar
satisfactoriamente con artificios matemáticos sencillos y fáciles de
manipular por el ser humano. Los modelos más simples, meros
planteamientos cualitativos (si pongo unos rodillos debajo de una
piedra, puedo transportarla más fácilmente que arrastrándola sobre la
tierra
), nos permiten construir herramientas primitivas con medios
pedestres y liberarnos de nuestras limitaciones de animales desnudos
hasta el punto de permitirnos emprender aventuras intelectuales más
profundas.
Con el tiempo, aprendemos a manejarnos simbólicamente con precisión y planteamos sencillos modelos cuantitativos que abren las puertas al diseño de artilugios cuyo funcionamiento detallado podemos predecir. Las cuentas son fáciles y los resultados son alentadores. Aumentar un poquito la sofisticación matemática de nuestros modelos produce unas ganancias espectaculares. La vida nos sonríe.
Nos volvemos más atrevidos y tratamos de saber más y construir ingenios más avanzados. Las matemáticas se complican, y aunque nuestra comprensión se sofistica y descubrimos atajos elegantes, los problemas se hacen tan grandes que exigen un trabajo excesivo para un solo ser humano. Afortunadamente, desarrollamos herramientas de cálculo y diseño automatizadas que alivian nuestra carga y nos permiten abarcar problemas inmensos. El desarrollo de estos medios hace que los problemas que antaño eran costosos de resolver se vuelvan inmediatos y que los que eran intratables se vuelvan alcanzables.
Demos un pequeño paso más allá. Busquemos una física un poquito más íntima y sofisticada o diseñemos una máquina un poquito más eficiente. De pronto, la naturaleza nos enseña los dientes. Las matemáticas se vuelven muy complicadas conceptualmente o, incluso si no es así, el volumen de cálculo se vuelve inmenso aunque sea por una mera cuestión de resolución. En lo que respecta a la fabricación de artefactos, no solamente tenemos esas dificultades computacionales en el diseño, sino que además alcanzar las prestaciones que buscamos exige unas tolerancias finísimas, unos procesos productivos muy costosos. Hay que invertir muchos recursos para ganar muy poco.
Es muy fácil predecir muchos fenómenos con una aproximación de una o dos décimas partes. A menudo, los cálculos se dejan tratar a mano en escasos minutos. Esta capacidad predictiva ya permite construir muchos ingenios modernos aceptablemente funcionales. Si queremos ir un poco más allá, a lo mejor podemos acercarnos incluso a unas pocas centésimas partes de incertidumbre sin que las necesidades de cálculo se disparen en exceso: podríamos tardar desde una fracción de segundo hasta algunos minutos en hacer los números necesarios con un ordenador personal. Algunos problemas especialmente benignos permiten incluso una mejor aproximación con estos medios, pero otros exigen muchos más recursos (a veces, la inversión incluso de meses de trabajo), quizá no tanto dedicados a su resolución como a su mero planteamiento. A partir de este punto, es habitual que los costes se disparen y haya que recurrir a medios de supercomputación (¡si es que son suficientes!) para aproximarnos a la realidad que queremos predecir (a las prestaciones del producto que estamos diseñando) quizá una centésima en casos malos, quizá una milésima en casos especialmente blanditos.
Categorías: Física
Cortador de tela
2016-01-08
Terminé recientemente un cortador rotatorio de tela con mango torneado en un ébano algo claro. Está construido alrededor de una cuchilla estándar de 45 mm de diámetro. Tiene menos prestaciones que los comerciales (carece de seguro), pero corta correctamente y tiene un aspecto que me agrada.

Cortador de tela.
El mango está torneado en ébano. Tiene un diámetro máximo de unos 25 mm y una longitud de unos 16 cm. La madera está desnuda: el único trabajo de acabado consistió en un lijado hasta grano 1500. La boca donde se sujeta el disco de corte está ranurada a 3,2 mm de ancho en fresadora vertical y tiene un taladro pasante según un diámetro para permitir la introducción de un tornillo M3 con el que sujetar el mandril de la cuchilla.
La cuchilla tiene un espesor de 0,3 mm y un diámetro interno de poco más de 8 mm. Como la boca del mango tiene un espesor de 3,2 mm, hay 2,9 mm de diferencia que hay que cubrir con algún tipo de mandril con el que sujetar la cuchilla. Hice este mandril en dos piezas: una arandela de 15 mm de diámetro exterior, 8,4 mm de diámetro interior y 1,4 mm de espesor; y una tuerca con rosca M3 y diámetro exterior 15 mm, espesor 1,4 mm, con un tetón concéntrico de 8,0 mm de diámetro y 1,7 mm de altura. Las dos piezas están torneadas en latón.

Fabricación del mandril.
El montaje no tiene mucha complicación. Hay que hacer pasar el tetón de la tuerca primero a través del agujero de la cuchilla y luego a través del agujero de la arandela, de manera que queda la cuchilla aprisionada entre las dos piezas de latón. Seguidamente, hay que introducir el conjunto por la boca del mango hasta alinear el agujero roscado de la tuerca con el taladro diametral. Con todo alineado, se sujeta la tuerca con un tornillo M3 de 12 mm de longitud.

Piezas del mandril.

Mandril sujetando la cuchilla.

Disco de corte ya instalado en el mango.
El disco tiene la libertad de movimiento adecuada para cortar fácilmente.

El cortador en acción.
Había que meter el cortador en algún sitio. Habría sido espléndido hacerle una caja de madera fina, pero la herramienta era un regalo que tenía que entregar con cierta urgencia, así que improvisé rápidamente algo con cartón de una caja de galletas y un poco de algodón.

El cortador en una caja improvisada rápidamente.
Categorías: DIY
Permalink: https://sgcg.es/articulos/2016/01/08/cortador-de-tela/
