Agosto de 2019
Calendario de artículos de de 2019
| lu | ma | mi | ju | vi | sá | do |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | |
Beyond Fried Chicken: Cartman se adelantó
2019-08-31
Beyond Meat produce sucedáneos de carne hechos con ingredientes de origen vegetal. Recientemente, pudimos leer que KFC, una cadena de restaurantes de comida rápida que sirve sucedáneo de sucedáneo de pollo hecho con ingredientes de origen avícola inicia un experimento comercial con Beyond feat para ofrecer Beyond Fried Chicken, un auténtico sucedáneo de pollo hecho con ingredientes de origen vegetal. ¡Un momento! ¿De qué nos suena esto? ¿Alguien ha dicho South Park?
Cartman se adelantó
Aquí vamos a destripar el argumento de una serie de ficción.
El indeseable personaje Eric Cartman de la teleserie de animación South Park, se adelantó a los acontecimientos en el episodio 7 de la temporada 21 (emitido originalmente el 8 de noviembre de 2017). En este episodio (y otros de la misma temporada), Cartman tiene una novia a la que trata horriblemente (eh, es Cartman). El muchacho gordito más grosero de Colorado trata de forma abusiva a su novia, pero como nunca es responsable de sus propios actos, achaca su inaceptable comportamiento a una pésima dieta. La pobre chica se las apaña para que Cartman pruebe una dieta vegana. Por supuesto, esta dieta no es del agrado de Cartman, quien siente un gran rechazo hasta que descubre el sucedáneo de carne Beyond Meat, muy similar a la porquería que hasta ahora engullía a diario. Ante semejante descubrimiento, Cartman enseña a su novia unos nuevos productos que supuestamente ha descubierto; entre ellos, Beyond KFC, una especie de premonición del recientemente anunciado Beyond Fried Chicken. ¡Ah, pero este Beyond KFC no es más que un cubo de KFC normal y corriente, hecho con ingredientes de origen animal! Todo es una trampa de Cartman para que su novia, que no sospecha nada, abandone el veganismo y se atiborre inconscientemente de la misma comida basura que él adora. Así de malo es Cartman.
Categorías: Miscelánea
Permalink: https://sgcg.es/articulos/2019/08/31/beyond-fried-chicken-cartman-se-adelanto/
Pato volando
2019-08-30
He aquí una fotografía de un pato en pleno vuelo. Quizá tendría que haberla tirado algo más rápida.

Fotografía de un pato volando.
Categorías: Fotografía
Permalink: https://sgcg.es/articulos/2019/08/30/pato-volando/
Pato
2019-08-28
He aquí una fotografía de un pato que va a lo suyo.

Fotografía de un pato.
Categorías: Fotografía
Permalink: https://sgcg.es/articulos/2019/08/28/pato/
Cuando Urkel nos previno de los deepfakes
2019-08-25
Los deepfakes son esos fotomontajes y videomontajes en los que, con ayuda de sistemas de aprendizaje automático, se cambia el aspecto de una persona, habitualmente para darle el aspecto de otra persona diferente. Son populares desde hace unos pocos años en aplicaciones muy diversas que abarcan lo lúdico inofensivo (intercambiar actores en una película, por ejemplo), lo lúdico más problemático (insertar el rostro de una persona famosa en una película pornográfica en la que nunca participó) y lo políticamente perverso (falsificar vídeos de personas influyentes para contar mentiras). A este ritmo, se hace difícil fiarse de lo que se ve grabado en vídeo. ¡Ah, pero si ya nos previno de ello hace décadas un personaje del que no sospecharíamos!
Urkel lo sabía
Aquí destripamos el argumento de un episodio una telecomedia. Avisado queda el incauto lector.
El 6 de diciembre de 1996 se estrenaba el capítulo 12 de la octava
temporada de la telecomedia de
situación Family
Matters (que llegó a España bajo el nombre de Cosas de
casa). Este episodio, cuyo título original fue The Jury,
era una parodia
de 12 Angry
Men (12 hombres sin piedad en España), el clásico
cinematográfico en el
que Henry Fonda
interpretaba a un miembro de un jurado que tenía que convencer a sus
compañeros para evitar que se condenara a un joven por un delito que
no cometió. En la versión de Family Matters, Steve Urkel
(interpretado
por Jaleel White)
emulaba al personaje de Fonda y trataba de salvar a un acusado de robo
que aparentemente había sido pillado en el acto delictivo por una
videocámara de seguridad. El caso era evidente para todos los
miembros del jurado menos para Urkel, para quien algo no terminaba de
encajar. Por supuesto, el bueno de Steve Urkel descubría la verdad:
la grabación había sido manipulada por el auténtico culpable. Como
demostración de la técnica, Urkel enseñaba dos vídeos manipulados con
la imagen de su apreciado amigo el grandullón Carl Winslow
(interpretado
por Reginald
VelJohnson): primero colocándolo en el lugar del crimen y después
colocando su rostro en el cuerpo de una moza en traje de baño
(ahora vean a esta truchita
, que decía en el doblaje español).
¡Ah, pero el auténtico culpable del robo había cometido un error en su
falsificación y se conservaba el reflejo de su rostro en un espejo!
Gracias a esta impecable demostración, Steve Urkel salvaba a un
inocente, señalaba al perpetrador real y se adelantaba al fenómeno de
los deepfakes varias décadas para enseñarnos que incluso las
grabaciones en vídeo hay que verlas con un sano escepticismo. ¡Bravo,
Steve!
Categorías: Miscelánea
Permalink: https://sgcg.es/articulos/2019/08/25/cuando-urkel-nos-previno-de-los-deepfakes/
La función de transferencia del espacio de color sRGB (4): más sobre la resolución de color (con 8 bits por canal)
2019-08-24
Recientemente vimos cómo el espacio de color sRGB usa una función de transferencia no lineal que agrupa los niveles de intensidad de forma variable. Más adelante vimos cómo reflejaba esta función de transferencia en la resolución de color. Falta conectar esta información numérica con la percepción visual humana en lo que se refiere a la capacidad de discernir diferentes niveles de intensidad luminosa. Recordemos, para ello, cómo se relaciona la intensidad real Ireal (normalizada para que el valor más grande sea la unidad) y la intensidad codificada In bits en el espacio sRBG cuando cada canal va representado por un número entero sin signo de n bits:
Ireal = In bits ⁄ [12,92×(2n−1)], 0 ≤ In bits < 0,04045×(2n−1);
Ireal = {[In bits+0,055×(2n−1)] ⁄ [1,055×(2n−1)]}2,4, 0,04045×(2n−1) ≤ In bits ≤ 2n−1.
También hemos de recordar la siguiente notación para el salto relativo que da el nivel de intensidad real cuando aumenta en una unidad el nivel discreto almacenado:
∆I(real) ⁄ Ireal = [Ireal(In bits+1)−Ireal(In bits)] ⁄ Ireal(In bits).
La profundidad de color más frecuente es n = 8. Trabajaremos con ese valor.
Percepción visual humana (versión muy simplificada)
El ser humano es capaz de distinguir con cierta soltura diferencias relativas de luminosidad del 2 %. Si las condiciones son buenas, es posible notar cambios más pequeños con algo de esfuerzo e incertidumbre, pero en muchas circunstancias los cambios perceptibles más pequeños son todavía más grandes. Quedémonos, por lo tanto, con cambios relativos del 2 % como objetivo para la resolución de la función de transferencia del espacio de color sRGB con 8 bits por canal. La siguiente curva muestra los niveles de intensidad que permiten una resolución más fina que ese 2 %:
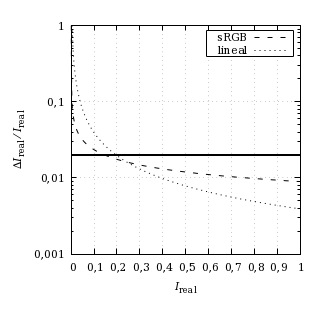
Saltos de intensidad relativos de sRGB con 8 bits por canal. La
línea gruesa horizontal marca el umbral
del 2 %. También aparecen los saltos de
intensidad relativos de un espacio de color lineal de 8 bits por canal.
Esta función de transferencia es satisfactoria cuando la intensidad real Ireal normalizada a la unidad es superior a aproximadamente 0,15: el 85 % superior de niveles de intensidad real tiene una resolución aceptable. El umbral está cerca de la mitad del rango de las intensidades codificadas y la función de transferencia de sRGB es muy similar a la perceptual, así que más o menos la mitad del rango subjetivo tiene una resolución aceptable.
Comparación con un espacio de color lineal
Un espacio de color lineal tiene la siguiente función de transferencia entre la intensidad almacenada In bits en números discretos de n bits y la intensidad real Ireal normalizada a la unidad:
Ireal = In bits ⁄ (2n−1).
Por lo tanto, los saltos relativos cuando el valor almacenado sube en una unidad son
∆Ireal ⁄ Ireal = 1 ⁄ In bits = 1 ⁄ [Ireal×(2n−1)].
Resulta que el salto relativo es más pequeño que el 2 % a partir de una intensidad real normalizada Ireal de 0,20 con una profundidad n = 8. En vez de un 85 % de niveles de intensidad con una resolución aceptable, el color lineal da un 80 %. En este sentido, la ventaja de sRGB no parece muy grande; ahora bien, la función de transferencia de sRGB da resultados mucho mejores en los niveles de intensidad más bajos.
Categorías: Fotografía, Informática
La función de transferencia del espacio de color sRGB (3): resolución de color
2019-08-18
Recientemente vimos cómo el espacio de color sRGB usa una función de transferencia no lineal que agrupa los niveles de intensidad de forma variable. Vamos a ver cómo afecta esto a la resolución de color. Recordemos, para ello, cómo se relaciona la intensidad real Ireal (normalizada para que el valor más grande sea la unidad) y la intensidad codificada In bits en el espacio sRBG cuando cada canal va representado por un número entero sin signo de n bits:
Ireal = In bits ⁄ [12,92×(2n−1)], 0 ≤ In bits < 0,04045×(2n−1);
Ireal = {[In bits+0,055×(2n−1)] ⁄ [1,055×(2n−1)]}2,4, 0,04045×(2n−1) ≤ In bits ≤ 2n−1.
Color de 8 bits por canal
Vamos, en primer lugar, con el caso más popular: n = 8. El salto de intensidad relativo de un valor al siguiente va de acuerdo con la siguiente curva:
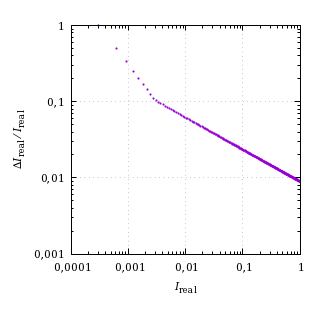
Saltos de intensidad relativos con 8 bits por canal.
La resolución es gruesa cuando las intensidades son pequeñas, especialmente en el tramo lineal, donde hay pocos valores.
Aproximación general
El salto relativo intensidad de un valor al siguiente es ∆Ireal ⁄ Ireal = [Ireal(In bits+1)−Ireal(In bits)] ⁄ Ireal(In bits). Como la función de transferencia es diferenciable en casi todo su dominio, la siguiente aproximación es bastante legítima:
∆Ireal ⁄ Ireal ≅ [dIreal(In bits) ⁄ dIn bits] ⁄ Ireal(In bits).
Unas pocas manipulaciones algebraicas llevan a las siguientes expresiones:
∆Ireal ⁄ Ireal = 1 ⁄ In bits, 0 ≤ In bits < 0,04045×(2n−1);
∆Ireal ⁄ Ireal ≅ 2,4 ⁄ [In bits+0,055×(2n−1)], 0,04045×(2n−1) ≤ In bits ≤ 2n−1.
La expresión del tramo lineal es, naturalmente, exacta.
Un poco más de álgebra lleva a las siguientes expresiones:
∆Ireal ⁄ Ireal = 1 ⁄ [12,92×(2n−1)×Ireal], 0 ≤ Ireal < 0,003131.
∆Ireal ⁄ Ireal ≅ 2,4 ⁄ [1,055×(2n−1)×(Ireal)1 ⁄ 2,4], 0,003131 ≤ Ireal ≤ 1.
Las anteriores expresiones son muy útiles a la hora de estimar los saltos relativos de intensidad. Convenientemente, se tiene la siguiente curvas universal:
(2n−1)×∆Ireal ⁄ Ireal = 1 ⁄ (12,92×Ireal), 0 ≤ Ireal < 0,003131.
(2n−1)×∆Ireal ⁄ Ireal ≅ 2,4 ⁄ (1,055×(Ireal)1 ⁄ 2,4), 0,003131 ≤ Ireal ≤ 1.

Curva universal de saltos relativos.
Categorías: Fotografía, Informática
La función de transferencia del espacio de color sRGB (2): rango dinámico
2019-08-17
Recientemente vimos cómo el espacio de color sRGB usa una función de transferencia no lineal que agrupa los niveles de intensidad de forma variable. Vamos a ver cómo afecta esto al rango dinámico, que es la relación entre el valor más grande que es posible representar y el valor no nulo más pequeño que es posible representar, en función de la profundidad de color. Recordemos, para ello, cómo se relaciona la intensidad real Ireal (normalizada para que el valor más grande sea la unidad) y la intensidad codificada In bits en el espacio sRBG cuando cada canal va representado por un número entero sin signo de n bits:
Ireal = In bits ⁄ [12,92×(2n−1)], 0 ≤ In bits < 0,04045×(2n−1);
Ireal = {[In bits+0,055×(2n−1)] ⁄ [1,055×(2n−1)]}2,4, 0,04045×(2n−1) ≤ In bits ≤ 2n−1.
Color de 8 bits por canal
En la práctica, lo más común es que la profundidad de color sea n = 8. El valor más alto es siempre Ireal = 1, mientras que el valor no nulo más bajo con esta profundidad de color es el correspondiente a I8 bits = 1: Ireal = 1 ⁄ (12,92×255). El rango dinámico, por lo tanto, es 12,92×255. En fotografía, el rango dinámico se mide a menudo en paradas o valores de exposición: simplemente el logaritmo en base 2 del anterior número, es decir, log2(12,92×255) ≅ 11,7. ¡El rango dinámico supera al de un espacio de color lineal de 8 bits en unas 3,7 paradas! Otra forma de verlo es la siguiente: para superar el rango dinámico que se consigue con el espacio de color sRGB con 8 bits por canal, hace falta un espacio lineal de color de 12 bits por canal.
Color de 4 bits o menos por canal
Cuando la profundidad de color es muy pequeña, la parte lineal de la función de transferencia no entra en acción. El valor no nulo más pequeño que es posible representar es Ireal = {[1+0,055×(2n−1)] ⁄ [1,055×(2n−1)]}2,4, mientras que el valor más grande que es posible representar es siempre Ireal = 1. Por lo tanto, el rango dinámico es {[1,055×(2n−1)] ⁄ [1+0,055×(2n−1)]}2,4, lo que en paradas o valores de exposición corresponde a 2,4×log2{[1,055×(2n−1)] ⁄ [1+0,055×(2n−1)]}, que es algo mayor que el valor correspondiente a un espacio de color lineal en unas 1,9 paradas cuando n = 2, unas 3,0 paradas cuando n = 3 y unas 3,6 paradas cuando n = 4. Para superar el rango dinámico que se consigue con el espacio de color sRGB con 2 bits por canal, 3 bits por canal o 4 bits por canal, hace falta un espacio lineal de color de 4 bits por canal, 6 bits por canal u 8 bits por canal.
Color de más de 4 bits por canal
En general, cuando el color es de más de 4 bits por canal, el valor no nulo más pequeño que es posible representar es Ireal = 1 ⁄ [12,92×(2n−1)], mientras que el valor más grande es siempre Ireal = 1, con lo que el rango dinámico es 12,92×(2n−1), lo que en paradas o valores de exposición es log2[12,92×(2n−1)] ≅ 3,7 + n. El rango dinámico está unas 3,7 paradas por encima del que se conseguiría con un espacio de color lineal. Para superar el rango dinámico que se consigue con el espacio de color sRGB con n bits por canal, hace falta un espacio lineal de color de n + 4 bits por canal.
Categorías: Fotografía, Informática
La función de transferencia del espacio de color sRGB (1): generalidades
2019-08-15
En el espacio de color sRGB, que es el que actualmente es más común en almacenamiento digital de imágenes, cada punto es la composición de tres colores primarios (rojo, verde y azul), pero las intensidades de estos colores no van codificadas tal cual, sino que van de acuerdo a una función de transferencia no lineal. Si la intensidad de cada color primario va de 0 (oscuridad) a 1 (máxima intensidad), con cuatro cifras significativas en los cálculos (que ya es mucho), la intensidad codificada IsRGB de cada color primario está relacionada con la intensidad real Ireal de dicho color primario mediante la siguiente relación:
IsRGB = 12,92 Ireal, 0 ≤ Ireal < 0,003131;
IsRGB = 1,055 (Ireal)1⁄2,4 − 0,055, 0,003131 ≤ Ireal ≤ 1.
La parte lineal de la curva, correspondiente a intensidades bajas, evita ciertos problemas numéricos que aparecen en el entorno del 0 cuando se usa una ley potencial.
A la inversa, la intensidad real Ireal de cada color primario está relacionada con la intensidad codificada IsRGB mediante la siguiente relación:
Ireal = IsRGB ⁄ 12,92, 0 ≤ IsRGB < 0,04045;
Ireal = [(IsRGB+0,055) ⁄ 1,055]2,4, 0,04045 ≤ IsRGB ≤ 1.

Función de transferencia del espacio de color sRGB.
Esta función de transferencia tiene un origen tecnológico histórico: se parece mucho a la respuesta de los monitores de tubo de rayos catódicos. También resulta que modela razonablemente bien la percepción visual humana típica.
Aproximación
Es posible aproximar la función de transferencia del espacio de color sRGB mediante una única función potencial. La siguiente ley da buenos resultados:
Ireal ≅ IsRGB2,2, 0 ≤ IsRGB ≤ 1.
El exponente 2,2 suele aparecer indicado con la letra griega γ en la literatura técnica al hablar de las leyes potenciales que se usan para codificar la luminancia o las intensidades de los colores primarios.
Profundidad de color de 8 bits por canal
Lo más frecuente es que los datos estén almacenados como números de 8 bits: cada valor almacenado puede ir de 0 a 255. La intensidad codificada IsRGB y el valor almacenado correspondiente I8 bits están relacionados de la siguiente manera:
IsRGB = I8 bits ⁄ 255.
Por lo tanto, la intensidad real Ireal y la intensidad almacenada en números de 8 bits I8 bits están relacionadas de la siguiente manera:
Ireal = I8 bits ⁄ (12,92×255), 0 ≤ I8 bits < 0,04045×255;
Ireal = [(I8 bits+0,055×255) ⁄ (1,055×255)]2,4, 0,04045×255 ≤ I8 bits ≤ 255.
Otras profundidades de color
Aunque el color de 8 bits por canal es muy común, no es lo único que existe. Si se usara color de 12 bits por canal, por ejemplo, la relación entre la intensidad real Ireal y la intensidad almacenada en números de 12 bits I12 bits, como los números de 12 bits llegan hasta 4095, sería la siguiente:
Ireal = I12 bits ⁄ (12,92×4095), 0 ≤ I12 bits < 0,04045×4095;
Ireal = [(I12 bits+0,055×4095) ⁄ (1,055×4095)]2,4, 0,04045×4095 ≤ I12 bits ≤ 4095.
En general, al usar n bits por canal, como con n bits es posible contar de 0 a 2n−1, la intensidad real Ireal está relacionada con la intensidad almacenada In bits mediante la siguiente relación:
Ireal = In bits ⁄ [12,92×(2n−1)], 0 ≤ In bits < 0,04045×(2n−1);
Ireal = {[In bits+0,055×(2n−1)] ⁄ [1,055×(2n−1)]}2,4, 0,04045×(2n−1) ≤ In bits ≤ 2n−1.
Categorías: Fotografía, Informática
Obturadores de plano focal de dos cortinillas y rolling shutter
2019-08-11
Muchas cámaras fotográficas modernas controlan el tiempo de exposición durante el que capturan la luz de una fotografía mediante un sistema de obturación mecánico de plano focal consistente en dos cortinillas que abren y cierran una ventana justo delante del sensor en el que se registra la imagen. En su modo de funcionamiento más sencillo, la exposición consiste en los siguientes pasos:
- De partida, el obturador está completamente cerrado mediante una primera cortinilla (la cortinilla frontal). Mientras el obturador está cerrado, el sensor no capta luz.
- Para comenzar la exposición, esta cortinilla frontal se retira y deja el sensor completamente expuesto a la luz.
- El obturador queda abierto durante cierto tiempo para que se produzca la exposición.
- Para terminar la exposición, una segunda cortinilla (la cortinilla trasera) sigue a la cortinilla frontal para ocupar su posición original y bloquear el paso de la luz.
- Finalmente, el obturador queda completamente cerrado de nuevo con la cortinilla trasera.
Las siguientes imágenes ilustran el mecanismo del obturador:

Estado inicial: el obturador está cerrado mediante la cortinilla
frontal.

Estado intermedio: el obturador está completamente abierto.

Estado final: el obturador está cerrado mediante la cortinilla
trasera.
El movimiento de las cortinillas lleva cierto tiempo. Un obturador típico no puede dejar el sensor completamente expuesto a velocidades de obturación más rápidas que 1 s ⁄ 250. Para conseguir tiempos de obturación más cortos (¡1 s ⁄ 8000, por ejemplo!), la cortinilla trasera ha de empezar a moverse antes de que la cortinilla frontal termine su recorrido. En ningún momento queda el sensor completamente expuesto, sino que hay una rendija entre las dos cortinillas que se desplaza y barre el sensor. El sensor solamente capta luz a través de la rendija, con lo que las distintas partes del sensor capturan la imagen en tiempos diferentes. Las siguientes ilustraciones explican este proceso de barrido:
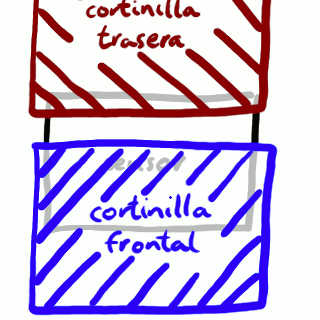
La rendija entre las cortinillas empieza a exponer la parte
superior del sensor.

La rendija entre las cortinillas ha avanzado hasta la parte
central del sensor.
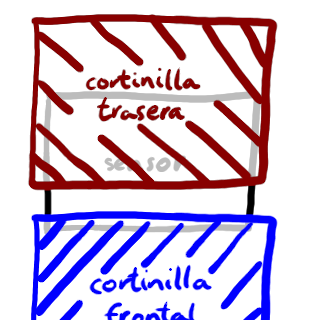
La rendija entre las cortinillas ha alcanzado la parte central del
sensor.
Reducir el tiempo de exposición sirve para que las fotografías queden menos expuestas cuando la luz es demasiado intensa, pero también sirve para congelar el movimiento: si el tiempo de exposición es demasiado largo, las imágenes salen movidas. Ahora bien, debido a la limitación práctica descrita anteriormente, a veces no es posible congelar satisfactoriamente el movimiento con iluminación continua, ya que aunque un tiempo de exposición muy corto sí elimina el emborronamiento de las imágenes movidas, el motivo fotografiado se desplaza apreciablemente conforme la rendija entre las cortinillas barre el sensor, con lo que la parte superior de la imagen muestra el motivo en una posición visiblemente distinta a la que muestra la parte inferior de la imagen. Al variar la dirección del movimiento, se producen efectos diferentes:
- Si el motivo se desplaza junto a las cortinillas, aparece alargado.
- Si el motivo se desplaza en contra de las cortinillas, aparece comprimido.
- Si el motivo se desplaza en dirección perpendicular a la del movimiento de las cortinillas, aparece distorsionado en cortadura, oblicuo.
- Si el motivo describe un movimiento más complicado (por ejemplo, circular), la distorsión puede ser bastante compleja.
A los mecanismos de obturación en los que el sensor registra la imagen no de forma simultánea, sino mediante un barrido, se les llama en inglés «rolling shutter». Las distorsiones descritas anteriormente son típicas del rolling shutter.
Para ilustrar este fenómeno, tomé unas fotografías del plato en rotación de una lijadora de disco. Marqué varios diámetros con cinta de carrocero para que se viera bien el efecto. Para empezar, veamos qué aspecto tiene el disco cuando su movimiento queda congelado. La siguiente imagen está sacada con un tiempo de obturación «lento» (el obturador permanece completamente abierto durante un tiempo), pero esto no importa, ya que la iluminación está proporcionada por un flash que destella durante un tiempo extremadamente corto:

Disco en rotación cuyo movimiento queda congelado con ayuda de
un flash. Los diámetros salen rectos.
Ahora veamos lo que pasa cuando el tiempo de obturación es «rápido» (el obturador nunca está completamente abierto, sino que deja abierta una rendija que barre el sensor):

Disco en rotación cuyo aspecto queda distorsionado como
consecuencia de las limitaciones del rolling shutter.
¡Los radios aparecen retorcidos! Esta distorsión es consecuencia del mecanismo de rolling shutter que tiene el obturador de plano focal cuando el tiempo de exposición es muy corto y no es posible exponer todo el sensor al mismo tiempo.
Categorías: Fotografía
La Electronic Frontier Foundation afirma que la persecución penal de Ola Bini se encuentra en el limbo por motivos políticos
2019-08-10
El experto en seguridad informática Ola Bini fue detenido en Ecuador hace unos meses. Actualmente se le acusa de algo así como asalto contra la integridad de sistemas informáticos, pero las autoridades no dan detalle alguno sobre el presunto delito (¡ni siquiera sobre alguna idea difusa sobre qué sistemas informáticos fueron presuntamente objeto de algún comportamiento delictivo!) y el caso se encuentra paralizado. La Electronic Frontier Foundation envió una delegación a Quito recientemente; las pesquisas indican que el caso está en el limbo por motivos políticos: las ramificaciones tanto de abandonar el caso como de continuar con él son difíciles de aceptar.
Categorías: Actualidad, Derechos
Cierra Linux Journal
2019-08-08
Linux Journal cierra por motivos económicos. Si esta noticia le resulta familiar al incauto lector, probablemente es porque ya hubo un aviso similar a finales de 2017. Esta vez, no obstante, se supone que no hay vuelta atrás. Se acaba con esto una época: la primera entrega de la veterana revista es de marzo de 1994.
Categorías: Actualidad, Informática
Permalink: https://sgcg.es/articulos/2019/08/08/cierra-linux-journal/
