La función de transferencia del espacio de color sRGB (3): resolución de color
2019-08-18
Recientemente vimos cómo el espacio de color sRGB usa una función de transferencia no lineal que agrupa los niveles de intensidad de forma variable. Vamos a ver cómo afecta esto a la resolución de color. Recordemos, para ello, cómo se relaciona la intensidad real Ireal (normalizada para que el valor más grande sea la unidad) y la intensidad codificada In bits en el espacio sRBG cuando cada canal va representado por un número entero sin signo de n bits:
Ireal = In bits ⁄ [12,92×(2n−1)], 0 ≤ In bits < 0,04045×(2n−1);
Ireal = {[In bits+0,055×(2n−1)] ⁄ [1,055×(2n−1)]}2,4, 0,04045×(2n−1) ≤ In bits ≤ 2n−1.
Color de 8 bits por canal
Vamos, en primer lugar, con el caso más popular: n = 8. El salto de intensidad relativo de un valor al siguiente va de acuerdo con la siguiente curva:
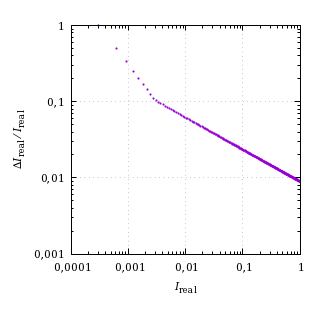
Saltos de intensidad relativos con 8 bits por canal.
La resolución es gruesa cuando las intensidades son pequeñas, especialmente en el tramo lineal, donde hay pocos valores.
Aproximación general
El salto relativo intensidad de un valor al siguiente es ∆Ireal ⁄ Ireal = [Ireal(In bits+1)−Ireal(In bits)] ⁄ Ireal(In bits). Como la función de transferencia es diferenciable en casi todo su dominio, la siguiente aproximación es bastante legítima:
∆Ireal ⁄ Ireal ≅ [dIreal(In bits) ⁄ dIn bits] ⁄ Ireal(In bits).
Unas pocas manipulaciones algebraicas llevan a las siguientes expresiones:
∆Ireal ⁄ Ireal = 1 ⁄ In bits, 0 ≤ In bits < 0,04045×(2n−1);
∆Ireal ⁄ Ireal ≅ 2,4 ⁄ [In bits+0,055×(2n−1)], 0,04045×(2n−1) ≤ In bits ≤ 2n−1.
La expresión del tramo lineal es, naturalmente, exacta.
Un poco más de álgebra lleva a las siguientes expresiones:
∆Ireal ⁄ Ireal = 1 ⁄ [12,92×(2n−1)×Ireal], 0 ≤ Ireal < 0,003131.
∆Ireal ⁄ Ireal ≅ 2,4 ⁄ [1,055×(2n−1)×(Ireal)1 ⁄ 2,4], 0,003131 ≤ Ireal ≤ 1.
Las anteriores expresiones son muy útiles a la hora de estimar los saltos relativos de intensidad. Convenientemente, se tiene la siguiente curvas universal:
(2n−1)×∆Ireal ⁄ Ireal = 1 ⁄ (12,92×Ireal), 0 ≤ Ireal < 0,003131.
(2n−1)×∆Ireal ⁄ Ireal ≅ 2,4 ⁄ (1,055×(Ireal)1 ⁄ 2,4), 0,003131 ≤ Ireal ≤ 1.

Curva universal de saltos relativos.
Categorías: Fotografía, Informática
