Ley de gravitación universal
2011-03-15
La ley de gravitación universal es un modelo muy útil para la predicción de la fuerza de atracción entre objetos con masa. No es el único modelo; por ejemplo, la relatividad general es otro modelo muy popular y de aplicación más general, pero extremadamente más sofisticado y costoso de utilizar.
Vamos a ver que podemos inventarnos la ley de gravitación universal mediante argumentos heurísticos sencillos sobre las propiedades que esperaríamos del campo gravitatorio. Tenemos la ventaja de saber de antemano que el modelo que vamos a deducir es muy bueno y permite realizar predicciones extremadamente acertadas de la realidad en casos tan interesantes como el movimiento de vehículos sobre la superficie terrestre, los satélites de comunicaciones y casi cualquier misión interplanetaria viable en estos momentos.
Este artículo surgía como uno aislado, pero ha pasado a formar parte de una serie sobre la ley de gravitación universal. Hay otros dos artículos que plantean formas alternativas de deducir el modelo:
- mediante ecuaciones de conservación o equilibrio para el potencial gravitatorio;
- mediante un principio de acción (o energía potencial total) estacionaria.
Deducción del modelo mediante argumentos heurísticos
Se comprueba experimentalmente que los objetos provistos de masa se atraen entre sí. La intensidad de esta atracción decae con la distancia y parece ser proporcional a las masas de los cuerpos tratados. De alguna manera, un cuerpo dotado de masa modifica el espacio y establece un campo de fuerza. Vamos a buscar un modelo razonablemente sencillo para el campo de fuerza generado por una masa concentrada en un punto —una masa puntual—:
- La fuerza gravitatoria F
a la que está sometida una masa puntual m atraída por otra masa puntual
M es proporcional a la propia masa
atraída:
F = m g,
donde g es la aceleración gravitatoria provocada por la masa M. Esta aceleración será el campo gravitatorio que estudiaremos en los siguientes puntos. - No tenemos motivos para postular la existencia de direcciones
privilegiadas. Supondremos que el campo gravitatorio se extiende con
simetría esférica con centro en la propia masa puntual y apuntando
hacia ésta. De esta manera, la magnitud del campo depende sólo de
la distancia a la masa puntual y no de si nos encontramos más al
norte, más al sur, más al este o más al oeste. Si el radio vector
de la masa puntual es r0,
el radio vector del punto en el que medimos el campo gravitatorio es
es r, la magnitud del campo es
g y el propio vector del campo es
g, tenemos la siguiente
relación:
g = −g ⋅ (r − r0) ⁄ |r − r0|. - Supondremos que la masa puntual está emitiendo o radiando el
campo gravitatorio en todo momento en todas direcciones.
Este campo se genera en la masa puntual y a partir de ahí se conserva.
Concretamente, el flujo total del campo a través de cualquier
esfera imaginaria centrada en la masa puntual ha de ser siempre el
mismo independientemente del radio de la esfera, ya que el flujo
es la cantidad total de campo que irradia la masa puntual en cada
momento. Como el flujo es proporcional
a la intensidad local g del campo
y a la superficie de la esfera S
por la que se extiende el campo, tenemos:
g ∝ 1 ⁄ S.
La superficie de la esfera es proporcional a su radio r, así que queda finalmente:
g ∝ 1 ⁄ r2. - La intensidad del campo es proporcional a la masa M:
g ∝ M.
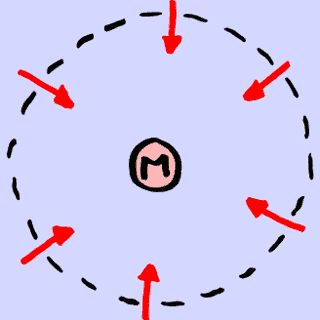
El campo gravitatorio apunta hacia la masa puntual fuente del
campo, tiene simetría esférica y su flujo a través de cualquier esfera
imaginaria que contiene la masa puntual es constante.
Si juntamos los puntos anteriores, obtenemos la
siguiente expresión para el campo gravitatorio g medido en un punto de radio vector
r y provocado por una masa
puntual M situada en un punto de radio
vector r0:
g(r) = −G M ⋅ (r − r0) ⁄ |r − r0|3.
La constante de proporcionalidad G
es universal: es la misma en todas partes. Nótese que, aunque la
distancia a la masa puntual aparece elevada al cubo en el denominador,
también figura linealmente en el numerador, de modo que la magnitud de
la aceleración gravitatoria es inversamente proporcional al cuadrado
de la distancia.

La masa puntual M atrae a la
masa puntual m. Una fuerza de
atracción igual en magnitud y opuesta en sentido actúa sobre la
masa puntual M.
Hemos postulado el campo gravitatorio producido por una masa
puntual. ¿Qué pasa si tenemos varias masas? No tenemos motivos
para suponer una interacción entre los distintos campos
gravitatorios, así que confiaremos en que se cumplirá el principio
de superposición: el campo total es igual a la suma de los campos
individuales producidos por cada una de las masas puntuales. La
aceleración provocada es, con notación evidente:
g(r) = ∑i−G Mi ⋅ (r − ri) ⁄ |r − ri|3.
De igual manera, si la masa está distribuida en el espacio con
densidad ρ(r0),
la aceleración gravitatoria es:
g(r) = ∫[−G ρ(r0) ⋅ (r − r0) ⁄ |r − r0|3] (dr0)3.
La anterior integral está extendida por todo el volumen del
cuerpo masivo que genera el campo gravitatorio.

Principio de superposición: el campo gravitatorio total es igual
a la suma de los campos gravitatorios individuales.
La fuerza gravitatoria F
sobre una masa puntual m situada en
el punto de radio vector r
es fácil de obtener mediante cualquiera de las anteriores expresiones
para la aceleración gravitatoria:
F = m g(r).
Si en vez de tener una masa puntual tenemos un cuerpo extenso
de densidad ρ(r)
entonces la fuerza gravitatoria total a la que está sometido este
cuerpo es fácil de obtener mediante una integral:
F = ∫ρ(r) g(r) (dr)3.
La anterior integral es doble cuando el campo gravitatorio está
generado por un cuerpo extenso:
F = ∫∫[−G ρ(r) ⋅ ρ(r0) ⋅ (r − r0) ⁄ |r − r0|3] (dr)3 (dr0)3.
Suponer masas puntuales es lo bastante preciso en muchos casos
prácticos, pero no siempre. En muchos casos, es posible aproximar
las integrales mediante sumas de momentos que convergen rápidamente
y permiten ahorrar mucho tiempo de cálculo; las aproximaciones de
masas puntuales no son más que estas sumas de momentos en las que
sólo retenemos los términos de orden más bajo.
El modelo que acabamos de deducir es precisamente la ley de la gravicación universal. Además de en casos diseñados por el hombre (como las misiones espaciales), se comprueba desde hace siglos que esta ley tan sencilla se ajusta con una excelente precisión a las observaciones realizadas sobre el movimiento de los planetas; esta precisión es tan buena que hace falta estudiar situaciones especialmente patológicas (como la precesión del perihelio de Mercurio) con medidas muy finas (realizadas a partir del siglo XIX) para encontrar discrepancias. ¡La formulación de leyes físicas no siempre es tan fácil!
Formas alternativas de llegar a la ley de gravitación universal
Hay muchas otras maneras de llegar a la ley de gravitación universal. Los siguientes artículos de esta serie explican varias:
- mediante ecuaciones de conservación o equilibrio para el potencial gravitatorio;
- mediante un principio de acción (o energía potencial total) estacionaria.
Categorías: Física
Permalink: https://sgcg.es/articulos/2011/03/15/ley-de-gravitacion-universal/
