Ley de gravitación universal (2)
2011-03-21
En el anterior artículo sobre la ley de gravitación universal vimos cómo deducir esta ley mediante argumentos sencillos de simetría geométrica, conservación y unas pocas suposiciones más. Hoy veremos una forma alternativa y muy elegante de deducir la ley de gravitación universal con la ayuda de un potencial y una ley de conservación.
Jugamos con la ventaja de saber que la ley que vamos a enunciar en realidad es bien conocida y se ajusta de forma excelente a muchísimos resultados experimentales. Si fuéramos a crear un modelo físico para un fenómeno poco estudiado, no tendríamos esta ventaja y probablemente tendríamos que modificar varias veces nuestro modelo hasta que éste predijera correctamente los resultados experimentales.
El presente artículo forma parte de una serie. Hay otros dos artículos que plantean formas alternativas de deducir la ley de gravitación universal:
- mediante un argumento sencillo de conservación y simetría;
- mediante un principio de acción (o energía potencial total) estacionaria.
El potencial gravitatorio
La técnica que vamos a emplear es algo más indirecta que
la del anterior artículo. En vez de trabajar sobre el campo
de aceleración gravitatoria (que es fácil de medir y de
efecto muy inmediato), lo haremos sobre el potencial
gravitatorio. Definimos el potencial gravitatorio φ(x) de modo que se
cumple la siguiente relación con la aceleración gravitatoria g(x):
g(x) ≡ −∇φ(x).
En la anterior ecuación, el operador ∇ es el gradiente. El signo menos se
utiliza bien porque los físicos son unos personajes crueles que
odian a los estudiantes, bien porque así no hay que usarlo en otros
momentos cuando toca trabajar con energías.
Trabajar con el potencial gravitatorio es muy cómodo porque se trata de un campo escalar (un campo que sólo tiene magnitud), mientras que la aceleración gravitatoria es más engorrosa porque se trata de un campo vectorial (un campo que tiene magnitud y dirección). Muchas veces, podemos resolver problemas físicos de gran interés trabajando sólo con el potencial gravitatorio; otras veces, necesitamos la aceleración gravitatoria, pero podemos realizar muchos cálculos intermedios con el potencial (con lo que ahorramos esfuerzo) y calcular la aceleración gravitatoria sólo cuando es necesiario.
La ecuación de conservación
Los experimentos indican que la fuerza de atracción gravitatoria está relacionada con la masa; por lo tanto, vamos a suponer que la masa es la fuente del campo gravitatorio. Supondremos también que el potencial gravitatorio obedece una ley de conservación: la cantidad total de campo que contiene un volumen cualquiera varía según lo que generan las fuentes encerradas en dicho volumen y el flujo que viaja a través de sus paredes, del mismo modo que la cantidad de de árboles en un bosque varía con los nuevos arbolitos que nacen de las semillas que caen de los árboles ya maduros (las fuentes) y los árboles jóvenes que introducimos desde el exterior y plantamos (el flujo a través de las paredes o la frontera del bosque).
En la mecánica newtoniana que estamos estudiando, el campo
gravitatorio se propaga instantáneamente. Esto quiere decir que
el campo puede cambiar con el tiempo si las masas que lo generan
se mueven, pero en todo momento estará en un estado de equilibrio
instantáneo. El campo generado por las fuentes (las masas) dentro
de un volumen arbitrario estará compensado, por lo tanto, por el
flujo a través de la frontera de dicho volumen. Si la intensidad
de las fuentes es s(x)
y el flujo a través de las paredes del volumen es f(x), la ecuación de conservación
o equilibrio tiene el siguiente aspecto:
∫∫∫Vs(x) dV + ∫∫Sf(x) dS = 0.
La integral triple está referida al volumen arbitrario V y la integral doble está referida
a la frontera S de dicho
volumen diferencial. El elemento diferencial de volumen es
dV y el elemento diferencial de
superficie es dS.
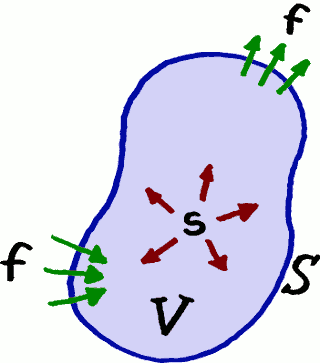
Equilibrio del campo gravitatorio en un volumen de control
arbitrario V (de color azul
claro) con frontera S (de color
azul oscuro). El campo generado por las fuentes s (las flechas de color rojo oscuro
indican cómo este campo es radiado por el interior del volumen)
es compensado por el flujo f a
través de las paredes (flechas de color verde).
La anterior ecuación es completamente inútil si no tenemos
ecuaciones constitutivas para relacionar la fuente y el flujo
con variables físicas como la distribución de masa y el campo
gravitatorio. Supondremos un modelo extremadamente
simple, tal que la fuente es proporcional a la densidad ρ(x) con la que la masa
está distribuida por el espacio:
s(x) ≡ A(x) ρ(x)
y el flujo es proporcional a la derivada del potencial gravitatorio
φ(x) en la dirección
normal n al elemento de
superficie (por fijar ideas, dirigida hacia el exterior del volumen):
f(x) ≡ B(n(x),x) n(x) ⋅ ∇φ(x).
Como no tenemos motivos para pensar que la forma en
la que se propaga la gravedad depende del lugar o de la
dirección, supondremos que el espacio es homogéneo e
isótropo, de modo que las variables de proporcionalidad
A(x) y B(n(x),x)
pasan a ser constantes independientes del punto y de la dirección. Si
reagrupamos las constantes de forma astuta, nos queda la siguiente
ecuación:
∫∫∫V4πG ρ(x) dV = ∫∫Sn(x) ⋅ ∇φ(x) dS.
La constante G es la constante de
gravitación universal; el término 4π no
está absorbido en su valor por meros motivos históricos y de comodidad
en otras expresiones (que no en ésta).
Podemos modificar la última ecuación para obtener otra un
poquito más conocida. Si aplicamos el teorema de la divergencia
para convertir la integral de superficie en una integral de volumen,
nos queda lo siguiente:
∫∫∫V4πG ρ(x) dV = ∫∫∫V∇2φ(x) dV.
En la anterior ecuación, el símbolo ∇2 es la laplaciana, es decir, la
divergencia del gradiente. Como el volumen de integración es
completamente arbitrario, obtenemos la siguiente ecuación diferencial:
∇2φ(x) = 4πG ρ(x).
Se trata de la conocidísima y estudiadísima ecuación de Poisson,
una ecuación elíptica que aparece en toda clase de problemas
de equilibrio.
Todas las anteriores ecuaciones están muy bien, pero hace falta una condición de contorno razonable para que el problema de encontrar el potencial gravitatorio dada una distribución de densidad esté bien planteado. Podemos suponer que en el infinito —mucho más lejos que el volumen de interés en el que queremos obtener el campo gravitatorio— no hay masa y la aceleración gravitatoria —la magnitud que podemos medir fácilmente— desaparece. De esta manera, el valor del potencial (no sus derivadas) no aparece ni en la ecuación de campo (cualquiera de las tres últimas) ni en la condición de contorno, así que tenemos el interesante resultado de que el potencial está definido salvo por un valor constante para todo el espacio.
El campo gravitatorio debido a una masa puntual: ley de gravitación universal
Una masa puntual M situada en el
origen de coordenadas tiene una distribución de densidad en el espacio
proporcional a una δ de Dirac:
ρ(x) = M δ(x).
La distribución δ de Dirac es tal
que:
∫∫∫Vδ(x) dV = 1
si el volumen contiene el origen x = 0;
0 si no.
Introduzcamos la anterior distribución de densidad en la ecuación
de campo:
∇2φ(x) = 4πG M δ(x).
La condición de contorno es la de aceleración gravitatoria nula en
el infinito:
límx→∞−∇φ(x) = 0.
La solución del problema tiene la siguiente forma:
φ(x) = C ⁄ |x| + D.
La constante D es, como
vimos antes, arbitraria y no tiene efecto en la aceleración
gravitatoria. Nos queda por determinar la constante C. Si usamos la primera forma de la
ecuación de campo (la de la fuente y el flujo) y elegimos un volumen
con el origen en su interior, deducimos con una simple integral que
la constante C es igual a −G M, de modo que el
potencial gravitatorio adopta el siguiente aspecto:
φ(x) = −G M ⁄ |x| + D.
La solución es singular y, en principio, no podríamos calcular su laplaciana en el origen, así que hay que entender la ecuación de Poisson de una forma generalizada que se reduce a la primera forma integral de la ecuación de campo (la de la fuente y el flujo).
La aceleración gravitatoria toma la siguiente forma, ya familiar:
g(x) = −G M x ⁄ |x|3.
La fuerza de atracción F
sobre una segunda masa puntual m situada en el punto x tiene el siguiente
aspecto:
F = −G M m x ⁄ |x|3.
Hemos obtenido la ley de gravitación universal que estábamos
buscando, de lo que se deduce que la ley de conservación y las
ecuaciones constitutivas que propusimos eran correctas.
Si la masa puntual M no está en el origen, podemos calcular la solución mediante una simple traslación. La fuerza para múltiples masas y masas distribuidas es fácil de calcular y la vimos en el anterior artículo sobre este tema. De forma alternativa, podemos calcular el potencial, derivarlo para obtener la aceleración y multiplicar por la masa de la partícula atraída para obtener la fuerza. Esta segunda forma de proceder, aunque es más indirecta, puede ser más cómoda que la primera en muchas ocasiones.
Formas alternativas de llegar a la ley de gravitación universal
El presente artículo forma parte de una serie. Hay otros dos artículos que plantean formas alternativas de deducir la ley de gravitación universal:
- mediante un argumento sencillo de conservación y simetría;
- mediante un principio de acción (o energía potencial total) estacionaria.
Categorías: Física
Permalink: https://sgcg.es/articulos/2011/03/21/ley-de-gravitacion-universal-2/
