Día del Número π
2012-03-14
El 14 de marzo es el Día del Número Pi, un día que celebra todo lo relacionado con una de las constantes matemáticas favoritas del mundo occidental: π, la razón entre la longitud de una circunferencia y su diámetro en una geometría plana euclídea. ¿Por qué el 14 de marzo? Porque este día, escrito en cifras decimales y con el mes delante del día, es 3-14, lo que es semejante a las tres primeras cifras de la expansión decimal de π: 3,14.
¿Qué se hace el Día del Número Pi? Podemos decorar la casa con las primeras cifras del número π, comer tartas (π en inglés se pronuncia igual que «pie», 'tarta'), organizar desafíos matemáticos diversos y contar historias relacionadas con el muy especial número que hoy nos ocupa.
En SGCG proponemos una actividad divertida para este día: estimar el valor del número π mediante un método empírico de Monte Carlo. La idea consiste en que, si inscribimos un círculo en un cuadrado y distribuimos puntos al azar dentro de este cuadrado, el número de puntos dentro del círculo dividido por el número total de puntos tenderá a la superficie del círculo dividida por la superficie del cuadrado, es decir, π ⁄ 4. Necesitamos dibujar una cuadrícula equiespaciada y, en cada cuadro, inscribir una circunferencia. Cada cuadro puede tener un lado de un par de centímetros, pero no mucho más ni mucho menos, ya que los cuadros han de ser pequeños para compensar el hecho de que probablemente no lograremos distribuir los puntos uniformememnte (sino que tenderemos a agruparlos en torno a un centro) y han de ser lo bastante grandes como para que los puntos no se confundan con las líneas. La siguiente figura lo ilustra:

Retícula hecha con un pulso mejorable.
Después de dibujar nuestra retícula, cerramos los ojos y pintamos muchos puntos sobre el papel. Desplazamos la mano de un lado para otro al azar para que los puntos acaben bien distribuidos. Finalmente, contamos los puntos que han caído dentro de los círculos y dividimos el resultado por el número total de puntos dentro de la cuadrícula. El cociente será una aproximación de la cuarta parte de π.
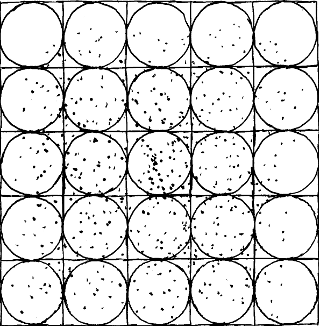
Resultado del experimento: una retícula llena de puntos.
Se aprecia que los puntos no están uniformemente distribuidos, pero
el hecho de haber usado una cuadrícula llena de círculos en vez
de un sólo cuadrado con un sólo círculo hace que tal cosa no sea
grave. Una mirada rápida indica que hay en torno a unos 435 puntos
dentro de los círculos y hay un total de en torno a 517 puntos en la
cuadrícula, así que sale un valor de 3,37,
lo que supone un error relativo de unas siete centésimas. No está
mal para lo burdo que es el experimento.
Categorías: Fechas, Matemáticas
Permalink: https://sgcg.es/articulos/2012/03/14/dia-del-numero-pi/
