La botella y la bodega de avión (3)
2013-07-20
Continuamos con los artículos sobre lo que pasaría con una botella cerrada y llena de algún líquido al transportarla en la bodega de un avión. Vimos que el principal problema es aguantar el salto de presión entre el ambiente de la bodega (inferior a la que hay en tierra porque la presurización es limitada) y la del interior de la botella (similar a la que había al cerrarla en tierra). Esta diferencia de presión puede estar en el entorno de los 25 kPa.
Hoy vamos a suponer que tenemos una botella de vidrio con un tapón de corcho. La botella aguanta sin problemas la diferencia de presión, pero podría suceder que la fricción contra la pared de vidrio no fuera suficiente para mantener en su sitio el tapón.
Aguante de un tapón de corcho
Vamos a hacer un cálculo rápido para estimar la máxima diferencia de presión que puede aguantar la fricción del tapón de corcho contra la pared interior de la botella antes de salir disparado. Este cálculo tiene unas inconsistencias internas que, afortunadamente, son pequeñas y hacen que el error cometido no sea muy grande.
En primer lugar, debemos tomar un modelo geométrico. Asumimos que la botella, que es perfrectamente rígida en comparación con el corcho, tiene una pared en forma de cilindro circular allí donde está el tapón. El propio tapón también es cilíndrico circular y es coaxial con la botella.
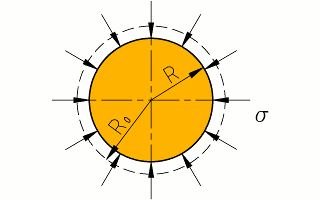
Compresión radial del tapón.
El tapón está metido a presión para que haga fuerza contra la pared
de la botella y así pueda tener buena fricción. Originalmente, el tapón
tenía un radio R0, pero
ahora está embutido con un radio R.
El corcho tiene un módulo elástico E
≈ 11 MPa; este módulo elástico relaciona la deformación
radial (el cambio relativo del tamaño del radio) y la presión σ con la que el tapón aprieta contra
la pared mediante esta expresión:
σ =
E (R0 − R) ⁄ R0.
El criterio de signos está escogido para que el valor sea positivo
cuando el tapón está apretado contra la pared, es decir, cuando
trabaja a compresión; lo habitual es asignar el signo negativo a la
compresión, no obstante. Por lo demás, el resultado sale de suponer
algunas cosillas que no son del todo descabelladas porque no queremos
afinar mucho: deformaciones infinitesimales; comportamiento elástico
lineal e isótropo; y un estado perfectamente axilsimétrico y plano.
Ya hemos aproximado la presión ejercida contra la pared,
σ. Si empujamos el tapón
a lo largo del cuello de la botella, aparece una fricción en la
superficie de contacto del corcho con el vidrio. Si hacemos poca
fuerza, el corcho se queda en su sitio. Conforme aumentamos la
fuerza, la fricción va creciendo hasta alcanzar un valor máximo;
tras alcanzar la fuerza correspondiente, la fricción deja de crecer
significativamente y el tapón desliza. La máxima tensión de
fricción τmáx
está relacionada con la presión ejercida contra la pared σ mediante un coeficiente de fricción
μ que, para la interfaz del vidrio
y el corcho, es más o menos igual a 0,5.
Con esto, la máxima tensión cortante de fricción es
τmáx =
μ σ.
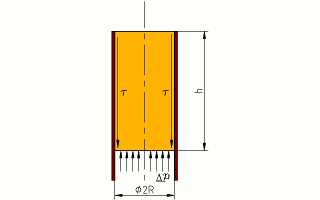
Equilibrio del tapón mediante fricción.
Ahora vamos a ver la tensión tangencial de fricción que
sería necesaria para retener el tapón en su sitio. Con una
diferencia de presión Δp
entre el exterior y el interior de la botella, la fricción
promedio τ es la que sale
de repartir por la cara en contacto con la pared (un cilindro de
altura h y circunferencia 2 π R) la resultante de aplicar
el salto de presión en el área de la base del tapón (un círculo
de área π R2):
τ
= Δp R ⁄ (2 h).
Esta tensión es positiva cuando se opone al salto de presión.
Supondremos que la presión en toda la pared es aproximadamente igual
al promedio, lo nos hace las cuentas muy fáciles.
Juntemos todo. Para que el tapón aguante en su sitio, la fricción
ha de estar por debajo del valor máximo:
τ < τmáx.
Con las expresiones derivadas anteriormente, esto queda así:
Δp R ⁄ (2 h)
<
μ E (R0 − R) ⁄ R0.
¡Un tapón de altura h = 4 cm
cuyo radio original fuera R0 = 1,05 cm
y cuyo radio embutido fuera R = 1 cm podría aguantar
un salto de presión de hasta 2,1 MPa!
Esto es mucho más grande que los 25 kPa
que podemos esperar. Un tapón real, con irregularidades y defectos,
aguantaría menos.
Otros artículos de la serie
- Introducción.
- Resistencia de la pared.
- Planteamiento general de un experimento para medir la capacidad del tapón.
- Experimento para medir la capacidad del tapón: caso de frenada instantánea.
- Experimento para medir la capacidad del tapón: caso de frenada gradual.
- Primer diseño del experimento.
- Diseño prometedor del dispositivo experimental.
Categorías: Física
Permalink: https://sgcg.es/articulos/2013/07/20/la-botella-y-la-bodega-de-avion-3/
