La botella y la bodega de avión (5)
2013-07-27
Continuamos con los artículos sobre lo que pasaría con una botella cerrada y llena de algún líquido al transportarla en la bodega de un avión. Vimos que el principal problema es aguantar el salto de presión entre el ambiente de la bodega (inferior a la que hay en tierra porque la presurización es limitada) y la del interior de la botella (similar a la que había al cerrarla en tierra). Esta diferencia de presión puede estar en el entorno de los 25 kPa.
Estamos diseñando un experimento para emular el efecto de la diferencia de presión en vuelo sobre el tapón de la botella. El experimento consiste en frenar repentinamente la botella para que su contenido se agolpe contra el tapón. Antes de plantear el experimento, tenemos que estimar la cuantía de la sobrepresión alcanzada en función de las condiciones de frenado. Empezamos estudiando el caso límite en el que detenemos la botella en un tiempo nulo.
Frenada instantánea
Asumamos en primer lugar que la botella es perfectamente rígida.
Entra en juego la acústica del contenido
líquido, que no es exactamente incompresible. Si el tapón aguanta
sin que se produzcan fugas, el líquido se frena repentinamente y esto
provoca una sobrepresión, lo que se conoce como un golpe de ariete.
La magnitud de esta sobrepresión está relacionada con la rapidez
v que tenía la botella justo
antes de frenarse y es fácil de modelar. Las perturbaciones en el
líquido se transmiten mediante ondas sonoras que viajan con velocidad
c. Digamos que todo transcurre
en un cilindro de sección S,
el cuello de la botella. En el instante de la frenada, se crea
una onda de compresión que se aleja del tapón. Un tiempo t después (tan corto que no se nota la
gravedad acelerando el fluido), la onda se ha movido una distancia
c t. Dentro del volumen
comprendido entre el tapón y el frente de onda, ha ido entrando
fluido con velocidad v y densidad
ρ (todavía sin perturbar
porque la onda no alcanza la frontera hasta el mismo instante t), de modo que tenemos una masa adicional
ρ v t.
Esta masa adicional se reparte en el volumen de longitud
c t y sección
S que ha barrido la onda,
es decir, la densidad se incrementa en una cantidad ρ v ⁄ c.
Los cambios de densidad están relacionados con los cambios de presión
mediante el módulo de compresibilidad K:
Δp =
K Δρ ⁄ ρ.
En nuestro caso, la sobrepresión es
Δp =
K v ⁄ c.
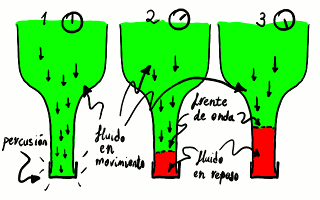
Propagación de una onda de presión en un cuello de botella
vista en tres instantes consecutivos (de izquierda a derecha).
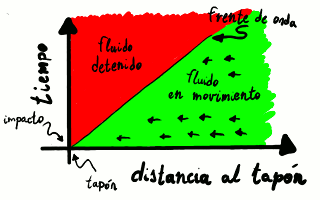
Diagrama de propagación de la onda. El eje de ordenadas es el
tiempo desde la frenada o impacto y el eje de abscisas es la distancia
al tapón que impide repentinamente el avance del fluido. Antes de ser
alcanzado por el frente de onda, el fluido no tiene noticia de la
presencia del tapón y sigue moviéndose.
Si el contenido no es muy diferente al agua, la velocidad del sonido c es próxima a 1,5 km s−1 y la compresibilidad K se parece mucho a 2,2 GPa. Haría falta una rapidez antes de la frenada muy pequeña, v = 17 mm s−1, para alcanzar el salto de presión de 25 kPa que queremos modelar. Este resultado hay que cogerlo con pinzas, por supuesto. Las hipótesis de frenada instantánea y botella perfectamente rígida son poco fieles a lo que pasa en el mundo, no obstante, así que este resultado no es más que una indicación de lo que podría alcanzarse mediante mecanismos sencillos y sin explotar la dinámica de la pared de la botella, que es flexible. Uno de los aspectos más fáciles de estudiar de la flexibilidad de la pared es una reducción de la rapidez con la que se propagan longitudinalmente las ondas debido a que la pared se estira al producirse la sobrepresión, con lo que aumenta la sección y el líquido se ajusta al nuevo espacio disponible.
La rigidez de la pared de la botella está caracterizada por el módulo elástico D del material, el diámetro D de la sección transversal y el espesor t de la pared. Sin deducirlo hoy, señalamos que la rapidez con la que se propagan las ondas largas se ve modificada de esta manera: pasa del valor c original de la velocidad del sonido en el líquido al valor modificado c ⋅ [1 + (K ⁄ E) (D ⁄ t)]−1 ⁄ 2. Una botella de vidrio (material de rigidez E = 68 GPa con un cuello cuya sección tiene un diámetro D = 25 mm y un espesor t = 5 mm ve bajada la rapidez de transmisión de ondas a unos 1,4 km s−1. En una botella de PET de pared delgada, las ondas se transmitirían más despacio, a unos pocos cientos de metros por segundo.
La formulación que usamos vale únicamente para ondas infinitesimales, con lo que modelar con esta hipótesis el efecto de la detención instantánea de la botella es como mínimo sospechoso de ser inadecuado. Esto es especialmente cierto en el caso de una botella muy flexible como una de PET de pared delgada. Incluso si se cumple la hipótesis de ondas infinitesimales, hace falta que el tiempo de frenado sea muy, muy corto. Si las ondas viajan a 1500 m s−2 y la distancia a recorrer en el seno líquido es de 25 cm (típica de una botella de dos litros), entonces las ondas van y vuelven en un tercio de milésima de segundo; la detención habría de tener lugar en un tiempo mucho más corto, de algunos microsegundos, para que fuera efectivamente instantánea.
Otros artículos de la serie
- Introducción.
- Resistencia de la pared.
- Estabilidad de un tapón de corcho.
- Planteamiento general de un experimento para medir la capacidad del tapón.
- Experimento para medir la capacidad del tapón: caso de frenada gradual.
- Primer diseño del experimento.
- Diseño prometedor del dispositivo experimental.
Categorías: Física
Permalink: https://sgcg.es/articulos/2013/07/27/la-botella-y-la-bodega-de-avion-5/
