La botella y la bodega de avión (8)
2013-07-31
Continuamos con los artículos sobre lo que pasaría con una botella cerrada y llena de algún líquido al transportarla en la bodega de un avión. Vimos que el principal problema es aguantar el salto de presión entre el ambiente de la bodega (inferior a la que hay en tierra porque la presurización es limitada) y la del interior de la botella (similar a la que había al cerrarla en tierra). Esta diferencia de presión puede estar en el entorno de los 25 kPa.
Estamos diseñando un experimento para emular el efecto de la diferencia de presión en vuelo sobre el tapón de la botella. El experimento consiste en frenar repentinamente la botella para que su contenido se agolpe contra el tapón. Ayer hicimos un primer planteamiento que no funcionaba bien por los materiales disponibles. El experimento que planteamos hoy es muy satisfactorio por ser fácil y barato y permitir un control bastante decente de la aceleración de frenada.
Segundo intento de diseño de un sistema de frenado
Volvemos a usar una cuerda de tender de polipropileno tan larga como la altura de la caída, pero esta vez no fija rígidamente al techo, sino atada a un listón de abeto rojo.
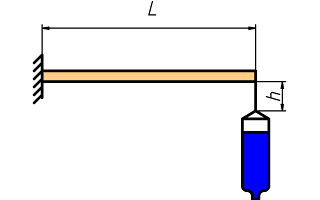
Dispositivo experimental: un listón de madera anclado a un banco
de trabajo y con la cuerda atada a un extremo.
El experimento consiste en dejar la botella a la altura del listón (es decir, con la cuerda sin extender) y dejarla caer repentinamente. La botella ha de frenar en vertical, así que hay que soltarla bien centrada bajo el punto de atadura de la cuerda al listón.
Hagamos un pequeño paréntesis para estudiar la cuerda. Como vimos en el artículo del pasado domingo, con una botella de dos litros, nuestro objetivo es alcanzar una carga de inercia (la suma de la aceleración experimentada por la botella y la aceleración gravitatoria) de unos 100 m s−2. Como la masa es de unos 2,0 kg, la fuerza que ha de aguantar la cuerda es de unos 200 N. Esta fuerza dividida por el área de la sección ha de superar la resistencia del material, que puede ser tan baja como 12 MPa. El valor mínimo del diámetro en estas condiciones está entre 4 mm y 5 mm; como las cuerdas vienen con diámetros en milímetros enteros, hay que conseguir una de al menos 5 mm. Si ancláramos rígidamente una cuerda de esta sección al techo, la aceleración conseguida no sería la de diseño, sino más del quíntuple, así que se rompería; es evidente que hace falta un anclaje apreciablemente flexible.
Vamos de vuelta al listón de madera. Este listón está anclado rígidamente en un extremo y tiene atada la botella en un punto alejado una distancia L. El listón tiene una sección rectángular de ancho b = 20 mm y altura t = 40 mm. La sección del listón tiene un segundo momento de área I = (1 ⁄ 12) b t3 ≈ 11 cm4; esta propiedad es importante en los cálculos porque guía el comportamiento a flexión. Ahora hay que saber las propiedades mecánicas. El material es abeto rojo, cuyo módulo elástico es E = 11 GPa y cuya resistencia es σu = 70 MPa.
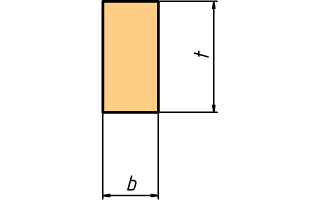
Sección transversal del listón.
Asumiremos que el listón se comporta como si no tuviera masa; es fácil comprobar que su inercia es pequeña en comparación con la de la botella.
El listón es mucho más flexible a flexión que la cuerda a tracción; como la cuerda cuelga del listón, toda la rigidez la aporta el último. La rigidez, que es la relación entre la carga que colgamos del listón y lo que esta carga desciende debido a que el listón se flexiona, es K = 3 E I ⁄ L3.
La masa es la misma que ayer y el sistema, cuando la botella llega abajo y tensa la cuerda, vibra igualmente con una frecuencia angular ω = (K ⁄ M)1 ⁄ 2. Esta vez, debido a la mayor flexibilidad (menor rigidez K), la frecuencia será mucho más baja.
Ayer vimos que la aceleración máxima de la botella cuando la rapidez de descenso justo antes de frenar es v y la aceleración gravitatoria es g0 ≈ 9,8 m s−2 es a = g0 [v ω ⁄ g0 + 1]1 ⁄ 2. La suma de esta aceleración y la gravitatoria es el valor objetivo a + g0 = 100 m s−2 necesario para que la sobrepresión en el tapón de la botella de dos litros alcance el valor deseado de unos 25 kPa. Podemos despejar el factor de carga objetivo n = v ω ⁄ g0, que en este caso ha de ser n = 8,9.
La tensión crítica σ a
la que está sometido el listón se da en las fibras más alejadas del
centro en el empotramiento. Esta tensión está relacionada con el
momento flector l P
de la carga máxima P =
M (a + g0 =
200 N mediante la expresión
σ =
L P t ⁄ (2 I).
Esta tensión ha de ser inferior a la resistencia del material σu para
que el listón no se rompa. De esto sale la siguiente restricción para
el brazo L:
L <
2 σu I ⁄ (P t).
Nos sale un brazo máximo muy largo: L
< 190 cm. Conviene que no nos aproximemos a la
resistencia del material; un brazo L
= 80 cm nos da una tensión máxima de 30 MPa, lo que es un buen margen.
La rapidez de la botella tras una caída desde una altura
h es v =
(2 g0 h)1 ⁄ 2.
Con esto y la frecuencia angular ω y el factor de carga n en función de las propiedades de las que
dependen, sale esta relación entre la altura de la caída (o longitud
de la cuerda) h y la distancia L de la cuerda al emptramiento (es decir,
el brazo):
h =
[n2 M g0 ⁄ (6 E I)] L3.
Si el brazo es L = 80 cm,
entonces sale una altura de suelta h = 11 cm. Estas dimensiones son muy
cómodas de manejar en un banco de trabajo en el que fijar el listón.
De propina: verificación de las simplificaciones de los cálculos
Entre los incautos lectores de esta página, hay algún ingeniero que aprecia estas cosas.
Dijimos que la inercia del listón es pequeña. Esto es fácil de comprobar. Si aplicamos una carga P en el extremo del listón de longitud L, la flecha allí es igual a L3 P ⁄ (3 E I) y la energía cinética máxima al oscilar a frecuencia angular ω es (1 ⁄ 2) ω2 M L6 P2 ⁄ (9 E2 I2). Si asumimos que la elástica del listón es casi la que sale a carga estática (que es la que usamos para calcular la deflexión en el extremo cargado), entonces la energía cinética máxima del listón sale de integrar la energía cinética de cada sección a lo largo de toda la longitud; el resultado es (1 ⁄ 2) ω2 11 ρ b t L7 P2 ⁄ (420 E2 I2). Lo único nuevo aquí es la densidad del material, 450 kg m−3. La energía cinética del listón dividida por la energía cinética de la botella es 33 ρ b t L ⁄ (140 M), es decir, como un 24 % de la masa del listón dividida entre la masa de la botella. La inercia del listón es un 3,4 % de la inercia de la botella y la frecuencia angular del sistema sería la correspondiente a sustituir la masa de la botella por ella misma incrementada en este 3,4 %, lo que supone reducir la frecuencia angular en un 1,7 %, algo muy pequeño, insignificante para nuestros fines.
También dijimos que la cuerda no aporta flexibilidad al sistema porque es tan inextensible que es como si la botella estuviera unida rígidamente al listón en el momento de alcanzar el punto de frenada. En efecto, para una carga P, la extensión de la cuerda es 4 h P ⁄ (Ecuerda π D2 = 4,3 μm N−1 P con Ecuerda = 1,3 GPa el módulo elástico de la cuerda. En cambio, la deflexión del extremo cargado del listón es 150 μm N−1 P, con lo que tener en cuenta la flexibilidad de la cuerda apenas supone un desplazamiento adicional del 3,0 %. Para calcular la frecuencia, sumaríamos las flexibilidades y sacaríamos el inverso de dicha suma para calcular la rigidez del sistema. Como la corrección es pequeña, el aumento del 3,0 % de la flexibilidad casi se corresponde con un descenso del 3,0 % de la rigidez y un descenso del 1,5 % de la frecuencia propia. El efecto combinado de esto y la inercia del listón supondría un descenso del 2,2 % en la frecuencia de oscilación. Ni la masa de la botella llena de líquido está determinada con tanta precisión, ni estamos valorando la inercia de la cuerda, ni estamos valorando la inercia del arnés que une la botella a la cuerda, ni estamos valorando muchos otros efectos, así que no tiene sentido refinar hasta este punto.
Otros artículos de la serie
- Introducción.
- Resistencia de la pared.
- Estabilidad de un tapón de corcho.
- Planteamiento general de un experimento para medir la capacidad del tapón.
- Experimento para medir la capacidad del tapón: caso de frenada instantánea.
- Experimento para medir la capacidad del tapón: caso de frenada gradual.
- Primer diseño del experimento.
Categorías: Física
Permalink: https://sgcg.es/articulos/2013/07/31/la-botella-y-la-bodega-de-avion-8/
