Cómo funcionan los sistemas de tramos de los impuestos progresivos
2017-04-04
Hay mucha incomprensión alrededor de los sistemas de tramos de los impuestos progresivos. Las retenciones que se establecen en los tramos son marginales, no totales. Esto significa que los impuestos pagados crecen de forma continua (sin saltos) con los ingresos. El tipo de un tramo indica la proporción de impuestos que paga cada unidad de ingresos adicional dentro de dicho tramo, no lo que pagaron las unidades de ingresos en tramos anteriores. La gráfica de impuestos pagados en términos absolutos frente a los ingresos tiene forma de línea quebrada, mientras que la del tipo efectivo (la proporción relativa de impuestos que se paga frente a los ingresos) tiene la forma de una curva convexa con quiebros. Veamos cómo funciona esto con más detalle.
Ejemplo de sistema con 2 tramos
Por ejemplo, si de 0 € a 100 € el tipo es del 10 % y a partir de los 100 % el tipo es del 20 %, esto no significa que si pasamos de cobrar 99 € brutos a cobrar 101 € brutos nos toque pasar de pagar 9,90 € de impuestos a pagar 20,20 € de impuestos; significa que los primeros 100 € pagan los 10 € que suponen el 10 % de impuestos del primer tramo y el restante (1 €) paga los 0,20 € que supone el 20 % de impuestos del segundo tramo sobre la parte que queda dentro del segundo tramo. Explícitamente, los impuestos absolutos r(i) en función de los ingresos brutos i con este hipotético sistema de tramos quedan como sigue:
r(i) = 0,1 ⋅ i si 0 ≤ i ≤ 100 €;
r(i) = 0,1 ⋅ 100 € + 0,2 ⋅ (i − 100 €) si 100 € < i.
El tipo efectivo de los impuestos, que es el impuesto absoluto dividido por los ingresos brutos, converge lentamente hacia el 20 % del último tramo: no alcanza el 19 % hasta los 1000 € de ingresos brutos, por ejemplo.
Ejemplo de sistema con 3 tramos
Ahora supongamos un sistema con 3 tramos:
- 10 % para los primeros 100 €;
- 15 % entre 100 € y 200 €;
- 20 % a partir de 200 €.
Esto significa que si se cobra como mucho 100 €, se paga un 10 % de impuestos; si se cobra entre 100 € y 200 €, los primeros 100 € salen por un 10 % de impuestos y lo que resta sale por un 15 % de impuestos; y si se cobra más de 200 €, los primeros 100 € pagan un 10 % de impuestos, los siguientes 100 € (lo que hay entre 100 € y 200 €) pagan un 15 % de impuestos y lo que resta a partir de 200 € paga un 20 % de impuestos.
Con la misma notación que antes, el impuesto absoluto queda como sigue:
r(i) = 0,1 ⋅ i si 0 ≤ i ≤ 100 €;
r(i) = 0,1 ⋅ 100 € + 0,15 ⋅ (i − 100 €) si 100 € < i ≤ 200 €;
r(i) = 0,1 ⋅ 100 € + 0,15 ⋅ (200 € − 100 €) + 0,2 ⋅ (i − 200 €) si 200 € < i.
Ahora haría falta tener unos ingresos i = 1500 € para que el tipo efectivo r(i) ⁄ i alcanzara el 19 %; el 20 % (que es el tipo marginal del último tramo) se alcanzaría con unos ingresos infinitos.
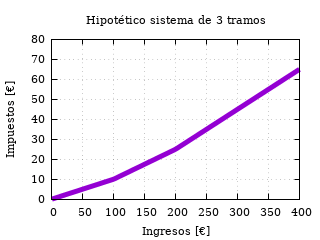
Impuestos pagados en el sistema de 3 tramos de ejemplo.
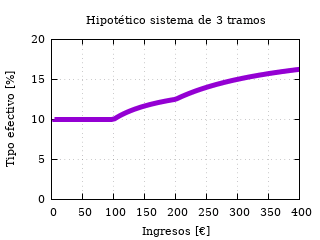
Tipo efectivo de los impuestos pagados en el sistema de 3 tramos de ejemplo.
Sistema de tramos general
En general, si se tiene un sistema con tramos determinados entre los niveles de ingresos (en orden creciente) {i0, i1, …, iN, iN+1} (i0 = 0, iN+1 = ∞) y tipos marginales {t0,1, t1,2, …, tN−1,N, tN,N+1} (defindos de manera que el tipo marginal tj,j+1 es la proporción de impuestos que paga cada unidad de ingresos entre el nivel ij y el nivel ij+1), los impuestos pagados son
r(i) = ∑n∈{0,N} tn,n+1 ⋅ [H(i−in)⋅H(in+1−i)⋅(i−in)+H(i−in+1)⋅(in+1−in)],
donde H(x) es la función escalón:
H(x) = 0 si x < 0;
H(x) = 1 si 0 ≤ x.
El tipo efectivo es
r(i) ⁄ i = ∑n∈{0,N} tn,n+1 ⋅ [H(i−in)⋅H(in+1−i)⋅(1−in ⁄ i)+H(in+1−in)⋅(in+1−in) ⁄ i].
El sistema tributario español se complica debido a la existencia de deducciones, pero el concepto del sistema de tramos es así de sencillo.
Categorías: Miscelánea
