Deformaciones mecánicas (2)
2017-08-29
En general, los cuerpos y medios materiales no permanecen perfectamente quietos, sino que se mueven y cambian de forma según transcurre el tiempo como consecuencia de sus interacciones con el entorno y de su propia dinámica interna. Esta serie de artículos trata sobre los cambios de forma o deformaciones.
Imaginemos que tenemos una pieza de longitud inicial li. La sometemos a un esfuerzo que provoca que se deforme hasta alcanzar una longitud lf. La pieza se ha deformado y nos proponemos cuantificar tal deformación. Hay varias maneras de hacerlo.
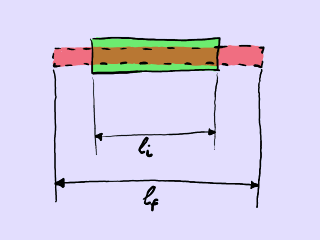
Pieza sujeta a una elongación. Pasa de tener una
longitud li (en línea
continua) a tener una
longitud lf (en línea de
trazos).
Deformación ingenieril o de Cauchy
La deformación ingenieril e es la elongación relativa a la longitud inicial:
e ≡ (lf − li) ⁄ li.
Como alternativa, podemos calcular una deformación similar a la ingenieril, pero tomando como referencia la longitud final, con la siguiente expresión:
(lf − li) ⁄ lf = e ⁄ (1 + e).
Deformación natural o logarítmica
Supongamos que dividimos el camino entre la longitud inicial li y la longitud final lf en una sucesión de incrementos infinitesimales dl de longitud. Para cada uno de estos incrementos infinitesimales alrededor de una longitud l (que vamos variando de la inicial a la final), la deformación ingenieril es
dl ⁄ l.
Si sumamos estas deformaciones a lo largo del camino, tenemos la deformación natural ε:
ε ≡ ∫dl ⁄ l = ln(lf ⁄ li) = ln(1 + e).
Deformación de Green-Lagrange
La deformación de Green-Lagrange hace referencia no a la longitud de la pieza, sino al cuadrado de dicha longitud. Hoy no veremos la justificación de esto, que tiene que ver con el concepto de distancia como forma cuadrática (como en el teorema de Pitágoras). Aceptemos por ahora que es interesante ver cómo se relacionan el cuadrado de la longitud final y el cuadrado de la longitud final. Definamos una forma cuadrática que relaciona el cuadrado de la longitud final está relacionado con el cuadrado de la longitud inicial:
Q ≡ (lf)2 ⁄ (li)2;
(lf)2 = (li) Q (li).
La deformación de Green-Lagrange εG es la mitad de lo que difiere el factor Q de la unidad:
εG ≡ (Q − 1) ⁄ 2 = [(lf)2 − (li)2] ⁄ [2 (li)2] = e (2 +e) ⁄ 2.
Deformación de Euler-Almansi
La deformación de Euler-Almansi εE es similar a la de Green-Lagrange, pero toma como referencia la longitud final:
εE ≡ (Q − 1) ⁄ 2 = [(lf)2 − (li)2] ⁄ [2 (lf)2] = e (2 + e) ⁄ [2 (1 + e)2].
Equivalencias de las diferentes definiciones de deformación
En el límite de deformaciones pequeñas, todas estas definiciones convergen al mismo valor que da la deformación ingenieril.

Diferentes definiciones de deformación.
Categorías: Física
Permalink: https://sgcg.es/articulos/2017/08/29/deformaciones-mecanicas-2/
