Deformaciones mecánicas (7)
2017-09-22
En general, los cuerpos y medios materiales no permanecen perfectamente quietos, sino que se mueven y cambian de forma según transcurre el tiempo como consecuencia de sus interacciones con el entorno y de su propia dinámica interna. Esta serie de artículos trata sobre los cambios de forma o deformaciones.
El tensor de deformación de Cauchy-Green
Vamos a usar la misma notación que en el artículo anterior. Volvemos a fijarnos en un segmento infinitesimal dx que, tras un movimiento, acaba convertido en el segmento infinitesimal dx'.
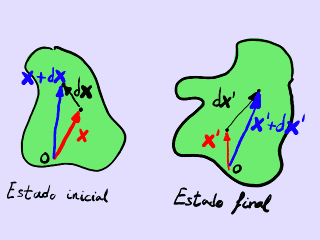
Deformación de un segmento infinitesimal.
El cuadrado de la longitud del segmento infinitesimal tras el movimiento es una forma cuadrática del cuadrado de la longitud del segmento infinitesimal antes del movimiento:
(dx')T ⋅ dx = dxT ⋅ [(∇x')T ⋅ ∇x'] ⋅ dx = dxT ⋅ C ⋅ dx.
El símbolo C denota al tensor de deformación de Cauchy-Green, cuya componente i,j-ésima en ejes cartesianos es
Cij ≡ ∑k(∂x'k ⁄ ∂xi) (∂x'k ⁄ ∂xj).
Como se aprecia, este tensor es simétrico.
El tensor de deformación de Cauchy-Green C está relacionado con el de Green-Lagrange ε. Recordemos que el tensor de deformación de Green-Lagrange sirve para construir una forma cuadrática que relaciona lo que cambia el cuadrado de la longitud del segmento infinitesimal con su valor inicial:
(dx')T ⋅ dx' − dxT ⋅ dx = dxT ⋅ (2 ε) ⋅ dx.
De esto se deduce la siguiente relación (en la que aparece el símbolo I como la matriz unidad):
ε = (1 ⁄ 2) (C − I).
Categorías: Física
Permalink: https://sgcg.es/articulos/2017/09/22/deformaciones-mecanicas-7/
