La función de transferencia del espacio de color sRGB (4): más sobre la resolución de color (con 8 bits por canal)
2019-08-24
Recientemente vimos cómo el espacio de color sRGB usa una función de transferencia no lineal que agrupa los niveles de intensidad de forma variable. Más adelante vimos cómo reflejaba esta función de transferencia en la resolución de color. Falta conectar esta información numérica con la percepción visual humana en lo que se refiere a la capacidad de discernir diferentes niveles de intensidad luminosa. Recordemos, para ello, cómo se relaciona la intensidad real Ireal (normalizada para que el valor más grande sea la unidad) y la intensidad codificada In bits en el espacio sRBG cuando cada canal va representado por un número entero sin signo de n bits:
Ireal = In bits ⁄ [12,92×(2n−1)], 0 ≤ In bits < 0,04045×(2n−1);
Ireal = {[In bits+0,055×(2n−1)] ⁄ [1,055×(2n−1)]}2,4, 0,04045×(2n−1) ≤ In bits ≤ 2n−1.
También hemos de recordar la siguiente notación para el salto relativo que da el nivel de intensidad real cuando aumenta en una unidad el nivel discreto almacenado:
∆I(real) ⁄ Ireal = [Ireal(In bits+1)−Ireal(In bits)] ⁄ Ireal(In bits).
La profundidad de color más frecuente es n = 8. Trabajaremos con ese valor.
Percepción visual humana (versión muy simplificada)
El ser humano es capaz de distinguir con cierta soltura diferencias relativas de luminosidad del 2 %. Si las condiciones son buenas, es posible notar cambios más pequeños con algo de esfuerzo e incertidumbre, pero en muchas circunstancias los cambios perceptibles más pequeños son todavía más grandes. Quedémonos, por lo tanto, con cambios relativos del 2 % como objetivo para la resolución de la función de transferencia del espacio de color sRGB con 8 bits por canal. La siguiente curva muestra los niveles de intensidad que permiten una resolución más fina que ese 2 %:
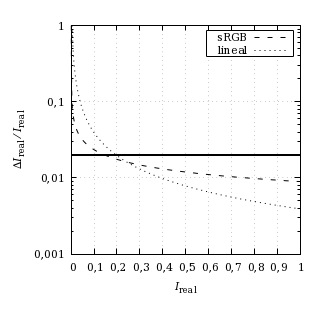
Saltos de intensidad relativos de sRGB con 8 bits por canal. La
línea gruesa horizontal marca el umbral
del 2 %. También aparecen los saltos de
intensidad relativos de un espacio de color lineal de 8 bits por canal.
Esta función de transferencia es satisfactoria cuando la intensidad real Ireal normalizada a la unidad es superior a aproximadamente 0,15: el 85 % superior de niveles de intensidad real tiene una resolución aceptable. El umbral está cerca de la mitad del rango de las intensidades codificadas y la función de transferencia de sRGB es muy similar a la perceptual, así que más o menos la mitad del rango subjetivo tiene una resolución aceptable.
Comparación con un espacio de color lineal
Un espacio de color lineal tiene la siguiente función de transferencia entre la intensidad almacenada In bits en números discretos de n bits y la intensidad real Ireal normalizada a la unidad:
Ireal = In bits ⁄ (2n−1).
Por lo tanto, los saltos relativos cuando el valor almacenado sube en una unidad son
∆Ireal ⁄ Ireal = 1 ⁄ In bits = 1 ⁄ [Ireal×(2n−1)].
Resulta que el salto relativo es más pequeño que el 2 % a partir de una intensidad real normalizada Ireal de 0,20 con una profundidad n = 8. En vez de un 85 % de niveles de intensidad con una resolución aceptable, el color lineal da un 80 %. En este sentido, la ventaja de sRGB no parece muy grande; ahora bien, la función de transferencia de sRGB da resultados mucho mejores en los niveles de intensidad más bajos.
Categorías: Fotografía, Informática
