Agosto de 2014
Calendario de artículos de de 2014
| lu | ma | mi | ju | vi | sá | do |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Ecuación del calor
2014-08-31
La ecuación del calor es una de las ecuaciones más famosas de la física matemática. Es la base para modelar la evolución de ciertos fenómenos difusivos como la transmisión de calor por conducción.
Hipótesis
Tenemos un medio:
- continuo;
- homogéneo;
- isótropo;
- estático (ni se desplaza ni cambia de forma);
- en equilibrio termodinámico local;
- en el que lo único que puede variar es la temperatura;
- en el que el único fenómeno que rige la transferencia de calor es la conducción;
- en el que el flujo de calor por conducción queda bien descrito mediante la ley de Fourier;
- en el que la energía térmica es directamente proporcional a la temperatura.
En lo que sigue, usaremos un sistema de referencia ligado al material. Como el medio se encuentra estático, la descripción lagrangiana y la descripción euleriana son idénticas.
Forma integral de la ecuación del calor
Asumimos que la densidad de energía interna u en un punto del cuerpo de densidad ρ a temperatura T es
u ≡ ρ c T.
La constante c es el calor específico del material (su capacidad calorífica por unidad de masa a volumen constante).
Cuando hay un gradiente ∇T de temperatura en un punto dado, se produce un flujo de calor q de acuerdo con la ley de Fourier:
q ≡ −k ∇T.
Si nos centramos en un volumen cualquiera V del cuerpo, vemos que su energía interna puede variar con el tiempo t:
(d⁄dt)∫∫∫Vu dV = ∫∫∫Vρ c dT ⁄ dt dV.
Esta variación se debe a algo. En virtud del primer principio de la termodinámica, esta variación con el paso del tiempo ha de deberse al flujo de calor que atraviesa perpendicular la superficie de frontera S del volumen:
(d⁄dt)∫∫∫Vu dV = ∫∫S−q ⋅ n dS = ∫∫Sk ∇T ⋅ n dS.
El símbolo n indica el vector normal a la superficie de frontera que apunta hacia el exterior. Como la normal apunta hacia el exterior, el flujo es positivo cuando sale energía del volumen, con lo que el efecto va con el signo opuesto. Si unimos las dos ecuaciones, nos queda una en función de la temperatura:
∫∫∫Vρ c ∂T ⁄ ∂t dV = ∫∫Sk ∇T ⋅ n dS.
Esta ecuación es una forma de expresar la ecuación del calor y se aplica a volúmenes cualquiera del cuerpo.
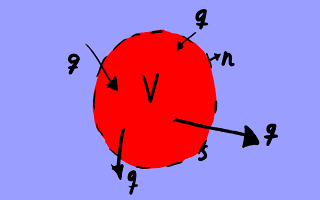
Flujo de calor a través de la
frontera S de un
volumen V. El
flujo q, que es vectorial,
solamente afecta en su componente según la dirección normal local
n.
Forma diferencial de la ecuación del calor
Partimos de la forma integral y aplicamos el teorema de la divergencia para que todas las integrales sean volumétricas:
∫∫∫Vρ c ∂T ⁄ ∂t dV = ∫∫∫Vk ∇2T dV.
El operador ∇2 es la laplaciana.
Podemos reagrupar los términos a la izquierda del signo de la igualdad:
∫∫∫V(ρ c ∂T ⁄ ∂t − k ∇2T) dV = 0.
Como esto se aplica a cualquier volumen de integración dentro del cuerpo, el integrando ha de ser exactamente nulo siempre:
ρ c dT ⁄ dt − k ∇2T = 0.
Podemos reunir todas las constantes en una a la que llamaremos α:
∂T ⁄ ∂t − α ∇2T = 0.
Esta ecuación es la forma diferencial de la ecuación del calor. Hay que complementarla con condiciones iniciales (la distribución de temperatura en un instante inicial) y condiciones de contorno (la temperatura o el flujo de calor en el contorno). Generalizar la ecuación del calor a otro número de dimensiones espaciales es elemental: solamente hay que usar la laplaciana ∇2 correspondiente.
Algunas propiedades de la ecuación del calor
La ecuación del calor es una ecuación parabólica. El calor se transmite al instante a cualquier distancia, pero los efectos solamente son grandes a distancias cortas y se aproximan a ser nulos a distancias grandes.
La ecuación del calor es muy agradecida. Tiende a alisar las irregularidades de las condiciones iniciales hasta alcanzar un estado estacionario que es independiente de la situación de partida; esto facilita el cálculo de soluciones aproximadas.
El problema de evolución hacia atrás en el tiempo está mal condicionado. En vez de suavizarse, las irregularidades se acentúan hacia atrás en el tiempo.
Categorías: Física
Permalink: https://sgcg.es/articulos/2014/08/31/ecuacion-del-calor/
Transferencia de calor por radiación (6): ley de Kirchhoff de la radiación térmica
2014-08-30
La emisividad y la absorbitividad de un material son propiedades que están fuertemente relacionadas mediante la ley de Khirchhoff de la radiación térmica. Esta ley establece la emisividad y la absorbitividad de un material cualquiera en equilibrio termodinámico son iguales. Como el seno del cuerpo emite y absorbe radiación térmica, la única manera de que el equilibrio termodinámico sea posible a una temperatura arbitraria es que cada partícula emita tanta radiación como absorbe, con lo que la emisividad tiene que igualar a la absorbitividad.
Emisividad y absorbitividad diferentes en tablas de propiedades de materiales
Hay tablas con propiedades de materiales que incluyen la emisividad y la absorbitividad. Estas tablas son muy útiles en la ingeniería. Sucede que en estas tablas figurar valores diferentes de la emisividad y la absorbitividad de un mismo material. Esto sucede como consecuencia de una simplificación. Sucede que en un material general, tanto la emisividad α como la absorbitividad ε dependen de la longitud de onda λ de la radiación. Esto queda escrito así con cierto abuso de notación:
ε ≡ ε(λ);
α ≡ α(λ).
Los valores que vienen en las tablas son promedios pesados adecuadamente con cierto espectro de emisión. Los materiales no emiten radiación térmica de cualquier manera, sino que tienen espectros de emisión en los que la cantidad de radiación emitida en cada frecuencia o longitud de onda λ y a cada temperatura T está bien definida. Tenemos un espectro de emisión E(λ,T). El valor de tabulado de la emisividad εpromedio suele estar pesado con el espectro de emisión del material Ematerial(λ,T) a una temperatura característica Tcaracterística que suele ser la temperatura ambiente:
εpromedio ≡ [∫ε(λ) Ematerial(λ,Tcaracterística) dλ] ⁄ [∫Ematerial(λ,Tcaracterística) dλ].
El valor de la absorbitividad, en cambio, suele venir pesado con el espectro de emisión de la fuente de radiación térmica más importante, que suele ser el Sol. El espectro del Sol es ESol(λ) (obviamos la dependencia con la temperatura porque el Sol no va a experimentar cambios notables en su temperatura a corto plazo) y la absorbitividad promediada es
αpromedio ≡ [∫α(λ) ESol(λ) dλ] ⁄ [∫ESol(λ) dλ].
El hecho de promediar con pesos diferentes es lo que explica esta falsa violación de la ley de Kirchhoff. El uso de valores promediados puede ser muy cómodo porque permite extender los cálculos con potencias emitidas regidas por la ley de Stefan-Boltzmann a cuerpos que no son los sencillos cuerpos negros. Cuando hay un enorme cuerpo emisor como el Sol, cuya irradiación es tan grande que la de otros cuerpos deja de ser significativa por comparación, podemos usar sin problemas una absorbitividad promedio pesada con el espectro del Sol. Si la temperatura de los cuerpos bajo estudio no varía mucho, es legítimo usar emisividades promediadas a la temperatura a la que se encontrarán aproximadamente. Estas dos aproximaciones con promedios simplifican enormemente unos cálculos que, de otra manera, se volverían tediosos al exigir el estudio de espectros detallados.
Categorías: Física
Transferencia de calor por radiacion (5): emisividad, absorbitividad y reflectividad
2014-08-29
Cuando diseñamos un equipo en el que la transferencia de calor por radiación es importante, debemos conocer algunas propiedades de sus superficies: la emisividad, la absorbitividad y la reflectividad. Hay otra propiedad, la transmitividad, que suele tener escasa importancia.
Emisividad
La emisividad ya la vimos anteriormente, pues figura en la ley de Stefan-Boltzmann. Es una medida de la radiación que emite un cuerpo en comparación con lo que emitiría un cuerpo negro. La potencia P emitida por la superficie A de un cuerpo gris a temperatura T es
P ≡ A ε σ T4.
La constante σ es universal, mientras que ε, la emisividad, es una constante adimensional que depende del tipo de cuerpo y que tiene el valor 1 en el caso de los cuerpos negros.
Absorbitividad
Los cuerpos reciben potencia calorífica que llega en forma de radiación electromagnética, pero en general no absorben toda la potencia perfectamente, sino solamente una parte. La proporción de la radiación total que un cuerpo absorbe es la absorbitividad, que suele indicarse con la letra griega α.
Reflectividad
Los cuerpos perfectamente negros absorben toda la radiación que les llega, pero son un caso especial. Generalmente, un cuerpo refleja parte de la radiación que incide sobre él. La proporción de la radiación que el cuerpo refleja es la reflectividad, que a menudo aparece indicada con la letra griega con la letra griega ρ.
Transmisividad
La transmisividad es la proporción de la radiación que incide sobre un cuerpo y que acaba transmitiéndose a través de él sin ser absorbida ni reflejada. Los cuerpos opacos tienen una transmisividad τ efectivamente nula.
Relación entre la absorbitividad, la reflectividad y la transmisividad
Como la radiación que incide sobre un cuerpo solamente puede absorberse, reflejarse o transmitirse, la suma de la absorbitividad, la reflectividad y la transmisividad, que son las proporciones de la radiación que acaban de un modo u otro ha de ser igual a la unidad:
α + ρ + τ = 1.
En los cuerpos opacos, la transmisividad es efectivamente nula y tenemos esta relación:
α + ρ = 1.
Categorías: Física
Transferencia de calor por radiación (4): deducción de la ley de Stefan-Boltzmann
2014-08-27
Vamos a deducir la ley de Stefan-Boltzmann para la transferencia de calor por radiación. Haremos uso de meras relaciones termodinámicas macroscópicas en combinación con un modelo adecuado sobre el comportamiento de un cuerpo negro. Esta prueba es esencialmente la que dio Boltzmann en su día.
Funcionamiento de un cuerpo negro
Un cuerpo negro es un objeto que absorbe perfectamente la radiación electromagnética, pero que también emite radiación por efectos térmicos. Un cuerpo negro se encuentra en equilibrio termodinámico con su propia radiación, que viaja por el interior del cuerpo en todas direcciones por igual (es decir, es isótropa). Cada partícula en el seno del cuerpo emite radiación que es absorbida por las partículas vecinas. Las partículas que están en la superficie emiten radiación que va hacia el interior del cuerpo, pero también hacia el exterior; esta última radiación escapa y lleva consigo energía procedente del cuerpo.
Deducción de la ley de Stefan-Boltzmann
Cuando un sistema termodinámico evoluciona de un estado de equilibrio a otro, puede experimentar un cambio en su energía interna U y en su entropía S. Si el sistema es un sistema simple compresible (como la radiación del interior de un cuerpo negro, que puede modificar su volumen si el cuerpo negro experimenta cambios), puede variar el volumen V. La variación de la energía interna de la radiación del interior del cuerpo negro está relacionada con la variación de la entropía y la variación del volumen mediante la siguiente ecuación:
dU = T dS − p dV.
El símbolo T está asociado a la temperatura y el símbolo p está asociado a la presión.
La energía interna de la radiación es una propiedad extensiva: es el producto de la densidad de energía u y el volumen V. Por lo tanto, si dividimos la ecuación de la energía por el volumen, tenemos una relación para la densidad de energía:
(∂⁄∂V)U = u = T (∂⁄∂V)S − p.
Por otra parte, como la radiación en el interior del cuerpo negro es isótropa, sabemos que la densidad de energía es igual al triple de la presión:
u = 3p.
La entropía S estorba. Hay unas relaciones termodinámicas, las relaciones de Maxwell, que nos permiten relacionar su derivada parcial con otra de la presión p:
(∂⁄∂VS = (∂⁄∂T)p.
Con esto, la ley de la energía queda expresada en términos de la presión y la temperatura:
3p = T (∂⁄∂T)p − p.
Esta ecuación diferencial admite la solución
p ∝ T4.
Por lo tanto, la intensidad I de la radiación, que es proporcional a la presión de la radiación, también es proporcional a la cuarta potencia de la temperatura:
I ∝ T4.
El flujo de la radiación que atraviesa una superficie cerrada es igual a la potencia neta emitida por los calientes contenidos en tal superficie. Esto significa que la intensidad de radiación emitida por un cuerpo negro y la potencia total radiada por tal cuerpo negro son proporcionales. Por lo tanto, la potencia que emite un cuerpo negro es proporcional a su temperatura elevada a cuatro: lo que dice la ley de Stefan-Boltzmann. Como la radiación solamente escapa a través de la superficie del cuerpo, la potencia radiada es proporcional a esta superficie.
Categorías: Física
Presión de la radiación isótropa
2014-08-26
Es posible deducir la ley de Stefan-Boltzmann mediante un razonamiento termodinámico macroscópico muy sencillo. Para poder realizar este razonamiento, primero necesitamos deducir la presión de la radiación isótropa. Deduciremos que la presión de la radiación es igual a la tercera parte de la densidad de energía.
Nos centramos alrededor de un determinado punto y fijamos un área infinitesimal dA. Definimos un sistema de coordenadas esféricas centrado en nuestro punto de estudio como en la figura:
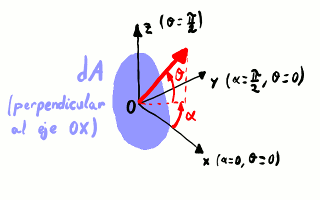
Sistema de coordenadas esféricas. Si miramos en una dirección
dada desde el punto bajo estudio, la elevación es el
ángulo θ y el acimut es el
ángulo α. La superficie
infinitesimal dA es perpendicular a
la dirección θ = 0, α =
0.
La radiación es isótropa, así que viene con la intensidad I (una potencia por unidad de superficie) de todas direcciones por igual. La energía contenida en un volumen
La radiación, isótropa, es igual a la superposición de frentes de onda de intensidad I que viajan en todas direcciones con rapidez c (la de la luz). Esta intensidad es un flujo de potencia por unidad de superficie y el flujo de potencia por unidad de superficie es lo mismo que la densidad u de energía por unidad de volumen multiplicada por la rapidez c con la que se propaga esta energía. Ya explicamos por qué era esto así en el artículo del teorema del transporte de Reynolds. La densidad de energía en un punto dado es igual a la resultante de la de todas las direcciones:
u = ∫dα∫θcos(θ) dθ I ⁄ c = 4 π I ⁄ c,
con el intervalo de integración definido de α = −π a α = π y de θ = −π ⁄ 2 a θ = π ⁄ 2.
La radiación electromagnética transporta cantidad de movimiento. La cantidad de movimiento de un fotón es igual a su energía dividida por la rapidez de la luz. Por lo tanto, la densidad p de cantidad de movimiento por unidad de volumen de un frente de onda es igual a
I ⁄ c2.
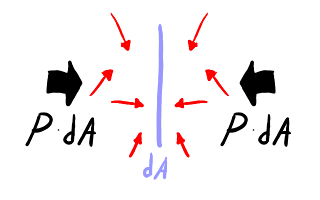
Equilibrio de fuerzas sobre la superficie elemental. La presión
ejercida por la radiación en una cara se contrarresta por la presión
ejercida por la radiación en la cara opuesta.
Hagamos como que la superficie dA es sólida. Como la radiación es isótropa, la superficie suporta una fuerza por un lado y la fuerza opuesta por el otro, de manera que la fuerza total es nula. La fuerza ejercida a un lado está relacionada con la presión P: es igual a P dA. Por otra parte, la fuerza se debe a la cantidad de movimiento que impacta y rebota por un lado de la superficie: es igual al doble de la cantidad de movimiento normal incidente. La componente tangencial no afecta a la cantidad de movimiento. La componente normal a la superficie dA de un frente de onda dirigido con acimut α y elevación θ es
(I ⁄ c2) ⋅ cos(α) ⋅ cos(θ).
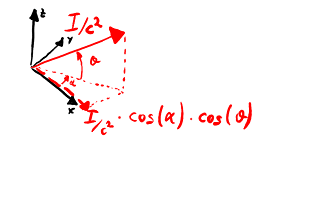
Densidad de cantidad de movimiento de un rayo y su componente
normal a la superficie (es decir, su proyección sobre el
eje OX: α =
0, θ = 0).
Esta cantidad de movimiento normal es transportada con velocidad normal
c ⋅ cos(α) ⋅ cos(θ).
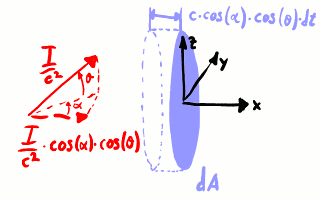
Transporte de la cantidad de movimiento normal de un rayo. Tras
un tiempo dt, ha incidido sobre la
superficie dA la cantidad de
movimiento normal contenida en el
volumen dA c cos(α) cos(θ) dt:
una cantidad de movimiento igual
a [(I ⁄ c2) cos(α) cos(θ)] [dA c cos(α) cos(θ) dt].
Esta cantidad de movimiento dividida por el intervalo de
tiempo dt es la cantidad de
movimiento normal de un rayo transportada perpendicularmente a la
superficie por unidad de tiempo.
La fuerza total en una de las caras de la superficie dA es igual al doble del resultado de la cantidad de movimiento normal transportada a la velocidad normal incidente desde esa cara de la superficie:
P dA = 2 dA ∫dα∫cos(θ) dθ [(I ⁄ c2) cos(α) cos(θ)] [c cos(α) cos(θ)] = (4 ⁄ 3) π dA I ⁄ c,
con el intervalo de integración definido de α = −π a α = π y de θ = −π ⁄ 2 a θ = π ⁄ 2. Por lo tanto, la presión es un tercio de la densidad de energía:
P = (4 ⁄ 3) π I ⁄ c = u ⁄ 3.
Este resultado es lo que buscábamos.
Categorías: Física
Transferencia de calor por radiación (2): ley de Stefan-Boltzmann
2014-08-22
Los cuerpos, pero el mero hecho de tener una cierta temperatura, tienden a emitir radiación electromagnética de una forma muy característica que está ligada a su naturaleza. La radiación se lleva energía térmica del cuerpo y sirve como vehículo para la transferencia de calor por radiación. Los detalles sobre esta radiación (su contenido espectral, por ejemplo) no están, en principio, bajo un control tan directo como la radiación emitida por una antena radiotransmisora. Esta emisión es un fenómeno térmico y tiene una forma muy particular. Los cuerpos negros emiten radiación electromagnética con una potencia P que depende de su temperatura T y de su superficie A de la siguiente forma:
P ≡ A σ T4.
Esta ley es conocida como la ley de Stefan-Boltzmann. La constante σ es universal para los cuerpos negros. La potencia emitida se distribuye superficialmente en los frentes de onda de la radiación electromagnética; la densidad superficial de potencia de la radiación emitida por cada partícula de un cuerpo acaba escalando con el inverso del cuadrado de la distancia a dicha partícula por una mera cuestión de conservación.
La ley de Stefan-Boltzmann queda generalizada fácilmente a cuerpos que no son cuerpos negros ideales con la ayuda de una constante de emisividad ε:
P ≡ A ε σ T4.
Este nivel de detalle es suficiente para cuerpos negros y grises. Cuando la dependencia con la frecuencia o la longitud de onda se complica con picos de absorción o emisión diversos, puede hacerse necesario tener en cuenta el contenido espectral con mayor o menor profundidad. Un cristal semitransparente, con sus direcciones y planos privilegiados para la propagación y para la polarización, puede requerir un estudio todavía más complicado. Afortunadamente, los casos prácticos de diseño de maquinaria suelen ser mucho menos exigentes.
Cada partícula de un cuerpo caliente emite radiación en todas direcciones y también recibe radiación de todas direcciones. La transferencia de calor por radiación a menudo es algo más costosa de modelar que la transferencia de calor por conducción debido a la propagación a distancia. El problema electromagnético exacto puede ser algo formidable de resolver porque las longitudes de onda relevantes pueden ser diminutas en comparación con el tamaño característico del sistema estudiado. Afortunadamente, en tales casos basta una aproximación de óptica geométrica en la que la radiación se propaga en forma de rayos que viajan en línea recta, con lo que basta calcular lo que se ve desde cada punto de interés mediante trazado de rayos.
La ley de Stefan-Boltzmann modela una forma de emisión de radiación electromagnética, pero no modela todas. Es posible transmitir calor por radiación con un comportamiento cualitativamente diferente con fuentes no térmicas como la del magnetrón de un horno de microondas. Aunque la radiación de estos dispositivos no tiene una distribución térmica, su efecto sobre los alimentos es uno de calentamiento. Generalmente, la radiación del magnetrón no recibe su energía en forma de calor, sino a través del trabajo macroscópico realizado en un generador eléctrico.
Categorías: Física
Permalink: https://sgcg.es/articulos/2014/08/22/transferencia-de-calor-por-radiacion-2-ley-de-stefan-boltzmann/
Transferencia de calor por radiación (1): principios básicos
2014-08-20
Mientras que los otros dos grandes modos de transferencia de calor (por conducción y por convección) exigen la presencia de un medio material para salvar distancias, la transferencia de calor por radiación puede realizarse a través del vacío debido a que el agente transmisor es la radiación electromagnética.
La radiación electromagnética no tiene masa, pero sí energía. Cuando un cuerpo emite radiación electromagnética, la energía que porta la radiación tiene que salir de alguna parte: sale del cuerpo emisor. Por lo tanto, los cuerpos se enfrían emitiendo radiación electromagnética. Por otra parte, cuando otro cuerpo absorbe esta radiación, recibe su energía, con lo que se calienta. Un cuerpo cualquiera se encuentra en todo momento emitiendo cierta cantidad de radiación y absorbiendo cierta cantidad de radiación incidente, con lo que el resultado puede ser, en función de las circunstancias, de ganancia neta de energía, de pérdida neta de energía o de equilibrio.
La radiación electromagnética tiene muchos parámetros. Es posible descomponerla en ondas con diferentes direcciones, diferentes frecuencias y diferentes polarizaciones. Los cuerpos no necesariamente absorben toda la radiación por igual, sino que en general pueden ser más absorbentes para determinadas frecuencias (lo que nos permite la visión en color), determinadas direcciones de propagación y determinados planos de polarización.
La radiación electromagnética que incide sobre un cuerpo y que el cuerpo no absorbe puede tener dos destinos: bien puede ser reflejada, bien puede atravesar el cuerpo si este cuerpo es transparente. Por su parte, la radiación absorbida calienta el cuerpo y el cuerpo, como consecuencia de ello, emite radiación electromagnética. Incluso los cuerpos completamente negros (que absorben la radiación perfectamente) emiten a su vez radiación electromagnética.
La radiación transporta energía y, como se distribuye por el espacio, esta energía también se distribuye por el espacio. Si congelamos el tiempo y nos fijamos en un determinado volumen, dentro de este volumen hay una cierta cantidad de energía. Si dejamos pasar el tiempo, la radiación abandona el volumen a través de la superficie que es su frontera: la radiación, al moverse, transporta una energía por unidad de tiempo y por unidad de superficie. Esta potencia por unidad de superficie es lo que se conoce como irradiación.
La transferencia de calor por radiación es especialmente importante en aplicaciones de satélites y sondas espaciales, ya que estos vehículos, al encontrarse en un medio que a afectos prácticos es el vacío, no tienen otra forma de disipar energía ni de recibir energía térmica del exterior. Otro caso interesante es el de la Tierra, que al fin y al cabo es un objeto de grandes dimensiones que se encuentra en el espacio. La principal fuente de calor por radiación en la Tierra es el Sol, cuya irradiación se sitúa en el entorno de 1,3 kW m−2 o 1,4 kW m−2 a la altura de la órbita terrestre. La vida en la tierra se beneficia de esta irradiación, que en conjunto da un flujo de potencia muy notable. Como la Tierra es aproximadamente una esfera de unos 6400 km de radio, la tierra recibe del Sol una potencia de entre 170 PW y 180 PW (el producto de la irradiación y la superficie frontal de la Tierra). La Tierra absorbe una parte de esta potencia, mientras que otra acaba emitiéndola al calentarse. El estado de la Tierra, a grandes rasgos, es casi estacionario, con lo que la potencia de radiación absorbida es casi igual a la potencia emitida.
Categorías: Física
Permalink: https://sgcg.es/articulos/2014/08/20/transferencia-de-calor-por-radiacion-1-principios-basicos/
Transferencia de calor por convección (3): convección natural y convección forzada
2014-08-18
La transferencia de calor por convección suele ser notablemente más efectiva que la transferencia de calor por conducción pura. Ahora bien, esta eficacia depende del movimiento del fluido que sirve para transportar calor por convección. Solemos hacer distinción entre dos tipos de convección: la convección natural y la convección forzada.
Convección natural
La convección natural sucede en el seno de un fluido que
originalmente se encuentra estático, pero que empieza a moverse como
mera consecuencia de la aparición de diferencias de temperatura. Este
movimiento se debe a cambios en las propiedades locales del fluido
como función de la temperatura, cambios que modifican las fuerzas a
las que está sometido. Puede suceder, por ejemplo, que el fluido se
vuelva menos denso al aumentar la temperatura; cuando el calentamiento
no es uniforme, la densidad tampoco lo es y se rompe el equilibrio
bajo la acción gravitatoria, con lo que el fluido empieza a circular
(se dice que el aire caliente asciende
…).
La convección natural está limitada por las diferencias de temperaturas: el movimiento se hace más enérgico conforme crecen las diferencias térmicas. Esta fuerte dependencia puede limitar notablemente la utilidad de la ley del enfriamiento de Newton como modelo predictivo, puesto que la «constante» de proporcionalidad que va multiplicada con la diferencia de temperatura para dar la potencia calorífica transferida puede depender tan fuertemente de la propia diferencia de temperatura en sí que la división en dos factores puede ser algo inútil. Podemos dejar el problema en evidencia con una notación semiformal. Asumamos que tenemos un cuerpo en el seno de un fluido. Hay una ΔT entre una temperatura característica del cuerpo y una temperatura característica del fluido. La potencia transferida del fluido al cuerpo es
P ≡ −h(ΔT) ⋅ ΔT
de acuerdo con el modelo de la ley de Newton. Hemos dejado escrita de forma explícita la dependencia funcional que tiene la «constante» de proporcionalidad h con la diferencia de temperaturas. En cuanto esta dependencia es medianamente importante relativa al factor lineal, la forma de la ley de Newton deja de tener interés práctico.
Un ejemplo de la convección natural es lo que sucede en el interior de un cazo donde se cuece algo de comida. El agua caliente de la parte inferior del cazo, mientras que el agua relativamente más fría de la superfice desciende. Este movimiento circulante permite un calentamiento más eficaz que el que habría si no se produjera y hubiera que contar solamente con la conducción.
La convección natural solamente puede darse cuando hay algún campo de fuerza cuyo efecto se ve modificado de alguna manera como consecuencia de los cambios de temperatura. El caso habitual es el del campo gravitatorio, que atrae con más intensidad las partes del fluido más densas y con menos intensidad las menos densas; como la densidad varía con la temperatura, tenemos ahí un mecanismo desencadenante de la convección natural. La convección natural deja debida a la gravedad deja de ser efectiva en las condiciones de microgravedad de un cuerpo en caída libre; tal es el caso que se da en los experimentos realizados en órbita, por ejemplo.
Convección forzada
Si en vez de partir de un fluido estacionario que se agita por el mero efecto de las diferencias de temperatura, forzamos el movimiento relativo con otros medios (con un ventilador en marcha, por ejemplo), tenemos lo que se conoce como convección forzada. Si la velocidad relativa de partida es lo bastante grande, la que sería provocada por los cambios de temperatura se hace irrelevante. La «constante» de convección del modelo del enfriamiento de Newton se hace muy insensible a la temperatura. Además de esto, como la velocidad relativa puede ser muy grande, la eficacia de la convección forzada puede ser mucho mayor que la de la convección natural. Esto es algo que se tiene en cuenta, por ejemplo, al diseñar sistemas de refrigeración para dispositivos electrónicos: cuando la refrigeración es por convección natural —refrigeración pasiva—, la superficie necesaria para disipar el calor puede ser muchísimo mayor que la necesaria con un sistema de refrigeración por convección forzada —refrigeración activa—.
La refrigeración por convección forzada puede funcionar cuando la convección natural ni siquiera es una opción, bien por cuestiones geométricas (quizá sería necesario un disipador enorme), bien por cuestiones físicas (como sucede en las cargas de pago de la Estación Espacial Internacional, donde la convección natural no es una opción por el entorno de microgravedad).
Categorías: Física
Transferencia de calor por convección (2): ley de Newton
2014-08-16
La transferencia de calor por convección puede ser muy complicada, pero a menudo es posible modelarla satisfactoriamente mediante una ley muy sencilla conocida como la ley del enfriamiento de Newton. Esta ley se aplica al enfriamiento o al calentamiento por convección de un cuerpo en contacto con un fluido. En vez de prestar atención al comportamiento detallado del sistema, la ley del enfriamiento de Newton se centra en alguna temperatura de referencia bien definida del fluido y una temperatura también bien definida del cuerpo a calentar o enfriar. La ley más sencilla que podemos imaginarnos es una en la que la potencia calorífica P que un cuerpo de temperatura característica Tc recibe mediante convección de un fluido de temperatura característica Tf es proporcional a la diferencia de ambas temperaturas:
P ≡ −h ⋅ (Tc−Tf).
Esto es la ley del enfriamiento de Newton. La potencia es positiva cuando el flujo de calor va del fluido al cuerpo y es negativa cuando va del cuerpo al fluido. La constante de proporcionalidad h depende de las características del sistema en cuestión y es positiva para que la potencia recibida sea postiva cuando el fluido está más caliente que el cuerpo. Esta ley es un análogo discreto de la la de Fourier para la conducción térmica.
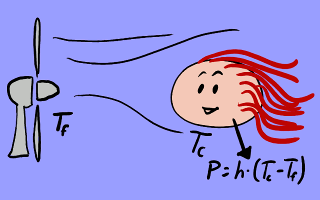
Esquema de la transferencia de calor por convección modelada
mediante la ley de Newton. Un ventilador sopla una corriente de aire
a temperatura Tf («fría»)
sobre una persona cuya temperatura
es Tc («caliente»), lo que
provoca que se transfiera una potencia
calorífica P
= h ⋅ (Tc−Tf)
del cuerpo de la persona al aire. El signo es el opuesto al usado
hace unos párrafos porque ahora estamos considerando el calor
transferido del cuerpo al fluido y no del fluido al cuerpo. El
proceso detallado de transferencia de calor sería algo complicado
simplemente por la geometría del cuerpo y la refrigeración evaporativa
que proporciona el sudor añade complejidad, pero el modelo de la ley
de Newton puede tener capacidad predictiva adecuada sobre la potencia
con la que se refrigera el cuerpo si no interesan los detalles.
La ley del enfriamiento de Newton es a menudo un buen modelo, pero en general no tiene más justificación que ser el término lineal de un desarrollo en serie de Taylor centrado alrededor de la temperatura característica del fluido o de la temperatura característica del cuerpo. A veces, no obstante, la ley de Newton es insatisfactoria y hay que buscar modelos más sofisticados.
La constante de convección térmica, h en la ecuación de unos párrafos más arriba, captura el comportamiento de un sistema. En un sistema dado, esta constante sale bien de cálculos teóricos, bien de medidas experimentales. Estas medidas experimentales, las famosas correlaciones empíricas, son de uso muy habitual; hay abundante literatura técnica con correlaciones empíricas aplicables a diversas geometrías y condiciones que son muy útiles al preparar nuevos diseños.
Categorías: Física
Permalink: https://sgcg.es/articulos/2014/08/16/transferencia-de-calor-por-conveccion-2-ley-de-newton/
Transferencia de calor por convección (1): principios básicos
2014-08-13
La convección es uno de los mecanismos de transferencia de calor más importantes. Se produce cuando la masa de un medio material se mueve y, con ella, la energía térmica.
Las partículas que conforman un medio material tienen una energía asociada. El calor en el seno de un sólido que permanece indeformable solamente puede transmitirse lentamente por conducción y, si el sólido tiene cierta transparencia, por radiación. Los fluidos son más interesantes: sus partículas se desplazan libremente y transportan consigo su energía térmica.
La convección en sí es el transporte que hacen las partículas del fluido al moverse (lo que en inglés se dice «advection»). La convección pura no sería técnicamente un mecanismo de transmisión de calor entre las partes constituyentes de un sistema material, ya que cada partícula de un fluido arrastraría su energía térmica de un lado para otro, pero sin transmitirla a las partículas vecinas. Lo que sucede es que la convección estrictamente pura no se da, sino que viene acompañada del mecanismo de transmisión de calor por contacto que es la conducción térmica. Este fenómeno mixto es lo que en inglés sí se conoce como «convection» y queda bien ilustrado con el chorro frío de un aparato de aire acondicionado: el chorro de aire viaja cierta distancia hasta entrar en contacto con un cuerpo caliente, momento en el que intercambia calor con este cuerpo rápidamente por conducción. Si el aire permaneciera quieto, habría que esperar mucho tiempo hasta que la conducción a larga distancia provocara cambios importantes en la temperatura. Vista así, la transferencia de calor por convección es una modificación de la transferencia de calor por conducción pura que permite que el flujo de calor sea mucho mayor al acercar las partículas que se encuentran a temperaturas diferentes (pues hay que recordar que el flujo de calor, de acuerdo con la ley de Fourier, se hace más grande conforme se hace más brusca la variación de temperatura a lo largo del espacio). Generalmente, la transferencia de calor por convección es notablemente más rápida que la transferencia de calor solamente por conducción.
Categorías: Física
Permalink: https://sgcg.es/articulos/2014/08/13/transferencia-de-calor-por-conveccion-1-principios-basicos/
Transferencia de calor por conducción (3): más sobre la ley de Fourier
2014-08-06
Presentamos la ley de Fourier de la conducción de calor en el último artículo. En última instancia, la ley de Fourier para la conducción de calor se deduce del comportamiento microscópico de los materiales y se verifica empíricamente. Hoy veremos, no obstante, cómo deducir la ley a partir de unas pocas hipótesis razonables.
Limitamos nuestro estudio al caso unidimensional. Este caso no es más que la abstracción de lo que sucede lejos del canto en una placa plana y delgada (de grandes dimensiones laterales en comparación con su espesor) de material homogéneo que dejamos a una cierta temperatura uniforme en una cara y a otra temperatura también uniforme en la cara opuesta. Solamente tenemos una coordenada espacial, x. Fijamos el origen x en el plano medio, tal que el material se extiende desde x = −h ⁄ 2 hasta x = h ⁄ 2, con h igual al espesor del medio material. Este medio solamente está sometido a transferencia de calor por conducción.
Dejamos el medio sometido a una diferencia de temperatura y esperamos hasta alcanzar un estado estacionario en el que la distribución de temperatura ya no varía. La temperatura en un extremo es T1 ≡ T(−h ⁄ 2) y la temperatura en el otro extremo es T2 ≡ T(h ⁄ 2). Definimos la temperatura media como Tmedia ≡ (T1+T2) ⁄ 2 y el incremento de temperatura como ΔT ≡ T2−T1. Si variamos estos parámetros, el flujo de calor q en el estado estacionario varía. Suponemos que el estado estacionario es único para un espesor dado y unas temperaturas en los extremos dadas. Con abuso de la notación, podemos expresar el flujo de calor como una función de la temperatura media y el incremento de temperatura:
q ≡ q(h,Tmedia,ΔT).
Si asumimos que el flujo de calor es una función analítica del incremento de temperatura, podemos hacer uso del siguiente desarrollo en serie de Taylor cuyos coeficientes son las funciones por ahora arbitrarias cm(h,Tmedia):
q ≡ ∑m≥0cm(h,Tmedia) ⋅ (ΔT)m.
Este desarrollo es demasiado general, pero podemos aplicarle restricciones. En primer lugar, si el incremento de temperatura es nulo, no hay flujo de calor en el estadio estacionario. Por lo tanto, el coeficiente c0(h,Tmedia) es idénticamente nulo. Además de esto, si restringimos el estudio a materiales que no tienen preferencia por el sentido de la diferencia de temperatura, el flujo de calor ha de ser una función impar de esta variable, con lo que todos los coeficientes pares se anulan:
q ≡ ∑m≥0c2m+1(Tmedia) ⋅ (ΔT)2m+1.
Los coeficientes han de tener valores tales que el flujo tenga siempre el signo opuesto al de la diferencia de temperatura. La condición más sencilla que se deduce de esto es que el coeficiente no nulo de orden más bajo ha de ser negativo. Para el caso convencional en el que el término lineal importa,
c1(h,Tmedia) < 0.
Ahora asumamos que el campo de temperaturas T(x) es una función analítica:
T(x) ≡ T(0) + ∑n≥1(dnT⁄dxn)(0) ⋅ xn ⁄ n!.
Si hacemos que el tamaño del dominio sea infinitesimal, tenemos los siguientes resultados:
límh→0Tmedia = T(0);
límh→0ΔT = (dT⁄dx)(0) ⋅ h.
Los productos de los coeficientes cm(h,Tmedia) y el incremento de temperatura han de ser finitos y, en general, no nulos. La única manera de lograr esto es hacer que se cumpla lo siguiente:
límh→0cm(h,Tmedia) = −km(Tmedia) ⁄ hm.
Los coeficientes km(Tmedia) son finitos, el de orden más bajo que no es nulo es positivo y los demás han de tener valores tales que el flujo sea siempre opuesto al gradiente de temperatura.
Con todo lo anterior, podemos expresar el flujo de calor de la siguiente manera:
q ≡ −∑m≤0k2m+1(T) ⋅ (dT⁄dx)2m+1.
Cuando los coeficientes no dependen de la temperatura, el estado estacionario es uno con una distribución lineal de temperatura (todas las derivadas son nulas salvo quizá la primera). Esto es fácil de comprobar sin más que igualar el flujo en dos puntos diferentes.
Si usáramos la ecuación del calor modificada con este flujo general, podríamos plantear condiciones adicionales. Es fácil demostrar que un flujo no lineal impide la obtención de soluciones autosemejantes de energía constante en un medio homogéneo. Este tipo de simetría, el de las soluciones autosemejantes, es una propiedad muy deseable que representa la ausencia de longitudes características en un medio homogéneo e infinito. Esto nos lleva a descartar los términos no lineales si buscamos este tipo de simetría, lo que nos permite recuperar la ley de Fourier que bien conocemos para el medio unidimensional:
q ≡ −k dT⁄dx.
Categorías: Física
