Tensiones o esfuerzos mecánicos (10)
2015-08-31
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. Vimos recientemente que las tensiones en un medio continuo quedan caracterizadas mediante un tensor simétrico de segundo orden: el tensor de tensiones. Este tensor de tensiones determina cuál es el vector tensión según la orientación con la que se mide. Ciertas orientaciones, las de los planos octaédricos, son muy notables.
Los planos octaédricos y las tensiones octaédricas
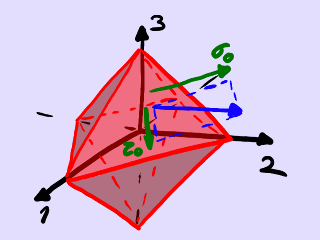
Planos octaédricos y tensiones octaédricas.
Vamos a tomar como sistema de referencia el definido por los ejes principales. En estos ejes, las componentes del tensor de tensiones adoptan la siguiente forma en representación matricial:
| σ1 | 0 | 0 |
| 0 | σ2 | 0 |
| 0 | 0 | σ3 |
Hay 4 direcciones diferentes que forman ángulos iguales con las direcciones principales o, si distinguimos entre las 2 orientaciones posibles para cada una de estas 4 direcciones, hay 8 posibilidades en total. Estas 8 orientaciones definen 8 planos como las 8 caras de un octaedro, así que son conocidas como las direcciones octaédricas. En ejes principales, las componentes de estas direcciones octaédricas son
(n1, n2, n3) = (±1 ⁄ √3, ±1 ⁄ √3, ±1 ⁄ √3).
Las componentes del vector tensión para una dirección octaédrica cualquiera son
(t1, t2, t3) = (±σ1±σ2±σ3) ⁄ √3.
El cuadrado de la magnitud del vector tensión es
|t|2 = (t1)2 + (t2)2 + (t3)2 = [(σ1)2+(σ2)2+(σ3)2] ⁄ 3.
La magnitud de la tensión octaédrica normal (la componente normal del vector tensión en la dirección perpendicular a un plano octaédrico) es
σo ≡ t1 n1 + t2 n2 + t3 n3 = (σ1+σ2+σ3) ⁄ 3 = σh = I1 ⁄ 3.
La tensión octaédrica normal es la tensión hidrostática, un tercio del primer invariante del tensor de tensiones.
La magnitud de la tensión octaédrica tangencial (la componente tangencial del vector tensión en la dirección perpendicular a un plano octaédrico) es
τo ≡ √[|t|2−(σo)2] = (1⁄3) √[(σ1−σ2)2 + (σ2−σ3)2 + (σ3−σ1)2] = √[(2⁄3) J2].
La tensión octaédrica tangencial es proporcional a la raíz cuadrada del segundo invariante del tensor desviador.
Aunque hay 8 planos octaédricos diferentes, las proyecciones normales y tangenciales del vector tensión medido en ellos son independientes del plano octaédrico elegido.
Categorías: Física
Permalink: https://sgcg.es/articulos/2015/08/31/tensiones-o-esfuerzos-mecanicos-10/
