Tensiones o esfuerzos mecánicos (18)
2016-06-28
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Hoy vamos a ver cómo cambiar de ejes de coordenadas en los estados de tensión plana.
Cambio de ejes cartesianos en tensión plana
En un estado de tensión plana, el tensor de tensiones solamente tiene tres grados de libertad en general. El vector tensión está contenido en un plano. En un sistema de ejes cartesianos x, y contenido en dicho plano, la tensión tiene solamente la siguientes componentes no nulas en general: {σxx, σyy, σxy} (la componente σyx es idéntica a la σxy debido a que el tensor de tensiones es simétrico).
Definamos ahora un segundo sistema de ejes x', y' también en el plano de tensión plana. Estos ejes forman un ángulo θ con los originales:
x' ≡ cos(θ) x + sin(θ) y;
y' ≡ −sin(θ) x + cos(θ) y.
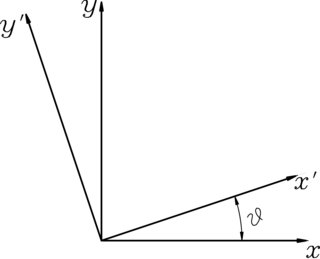
Sistemas de ejes.
Sabemos cómo pasar las componentes del tensor de tensiones de un sistema de ejes a otro. De forma explícita, el cambio entre estos ejes es así:
σ'x'x' = {[1+cos(2θ)] ⁄ 2} σxx + {[(1−cos(2θ)] ⁄ 2} σyy + sin(2θ) σxy;
σ'y'y' = {[1−cos(2θ)] ⁄ 2} σxx + {[(1+cos(2θ)] ⁄ 2} σyy − sin(2θ) σxy;
σ'x'y' = [sin(2θ) ⁄ 2] (σyy−σxx) + cos(2θ) σxy.
Se trata de unas expresiones sencillas y convenientes de tener a mano.
Categorías: Física
Permalink: https://sgcg.es/articulos/2016/06/28/tensiones-o-esfuerzos-mecanicos-18/
