Tensiones o esfuerzos mecánicos (20)
2016-08-31
La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Hace un par de meses vimos cómo cambiar de ejes de coordenadas en los estados de tensión plana. Hace algo más de tiempo, introdujimos los círculos de Mohr. Resulta que los círculos de Mohr tienen una aplicación especial en el caso de tensión plana.
La circunferencia de Mohr en tensión plana
Escojamos un punto de un medio material. En ese punto, en un sistema de referencia dado de ejes cartesianos x, y, z, el tensor de tensiones tiene componentes σxx, σyy, σzz, σxy, σxz y σyz (además de las del otro lado de la diagonal que se deducen inmediatamente debido a que el tensor de tensiones es simétrico). En este experimento mental, el estado es de tensión plana y los ejes están elegidos de manera que
σzz = σxz = σyz = 0.
Las componentes normal σ y tangencial τ del vector tensión medido en un plano orientado un ángulo θ relativo al sistema de referencia en el que se da el tensor de tensiones de referencia obedecen las siguientes expresiones:
σ − (σxx+σyy) ⁄ 2 = cos(2θ) (σxx−σyy) ⁄ 2 + sin(2θ) σxy;
τ = sin(2θ) (σyy−σxx) ⁄ 2 + cos(2θ) σxy.
Salen sin más de sustituir σx'x' con la tensión normal σ y σx'y' con la tensión tangencial τ en las ecuaciones de cambio de ejes y mover algún elemento. En el plano σ,τ, estas ecuaciones describen una circunferencia. Otra forma de verlo es si elevamos al cuadrado ambas igualdades y las sumamos, con lo que obtenemos lo siguiente:
[σ−(σxx+σyy)]2 + [τ]2 = [(σxx−σyy) ⁄ 2)]2 + [σxy]2.
Esta expresión no depende del ángulo θ y es la ecuación de una circunferencia. El centro de esta circunferencia está en el punto
(σxx+σyy) ⁄ 2, 0.
El radio es
{[(σxx−σyy) ⁄ 2]2
+
[σxy]2}1⁄2.
Si las tensiones de partida para la construcción de la
circunferencia de Mohr son las
principales σ1 y
σ2 (tales que la
primera es mayor o igual que la segunda), entonces el centro de la
circunferencia es el punto
(σ1
+ σ2) ⁄ 2, 0
y el radio es
(σ1 − σ2) ⁄ 2.
Si las dos tensiones principales son iguales, la circunferencia de
Mohr tiene radio nulo y el estado es uno de «presión hidrostática
bidimensional».
En las ecuaciones paramétricas, el ángulo que entra en las
funciones trigonométricas no
es θ,
sino 2θ. Las componentes del
vector tensión realizan dos ciclos completos al dar una vuelta, como
es de esperar, ya que las tensiones representan fuerzas por unidad de
superficie contrapuestas.
En el próximo artículo de la serie veremos cómo usar la
circunferencia de Mohr como herramienta gráfica de cálculo.
Categorías:
Física
Permalink:
https://sgcg.es/articulos/2016/08/31/tensiones-o-esfuerzos-mecanicos-20/
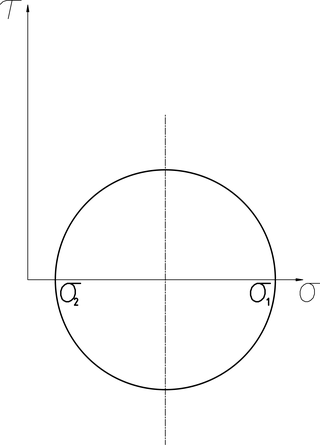
Circunferencia de Mohr.
