El modelo epidemiológico SIR (4)
2020-03-20
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia, así como el comportamiento de la proporción de infectados en esta fase inicial. Hoy veremos cómo relacionar las variables sin necesidad de integrar en el tiempo.
Recordemos que el modelo sigue a lo largo del tiempo t la evolución de la proporción de susceptibles S(t), la proporción de infectados I(t) y la proporción de recuperados (inmunes y fallecidos) R(t) mediante el siguiente sistema de ecuaciones diferenciales ordinarias:
dS ⁄ dt = −(R0 ⁄ tI) S I;
dI ⁄ dt = (R0 ⁄ tI) S I − (1 ⁄ tI) I;
dR ⁄ dt = (1 ⁄ tI) I.
El parámetro R0 es el número medio de contagios por infectado cuando toda la población es susceptible y el parámetro tI es el tiempo medio que permanece un paciente infectado.
Si los parámetros son constantes, el sistema es autónomo y muy fácil de analizar. Podemos relacionar las variables entre sí sin necesidad de conocer la evolución temporal. Del sistema de ecuaciones original se deduce el siguiente:
dI ⁄ dS = −1 + 1 ⁄ (R0 S);
dR ⁄ dS = −1 ⁄ (R0 S).
Basta integrar para obtener las relaciones entre las variables:
I(t) − I(0) = S(0) − S(t) + (1 ⁄ R0) log[S(t) ⁄ S(0)];
R(t) − R(0) = −(1 ⁄ R0) log[S(t) ⁄ S(0)].
Otra forma de escribir las anteriores ecuaciones es la siguiente:
I(t) − I(0) = S(0) {1 − e−R0 [R(t)−R(0)]} − R(t) + R(0);
S(t) = S(0) e−R0 [R(t)−R(0)].
Las relaciones están definidas siempre que S(t) ≤ S(0), I(t) ≥ 0 y R(t) ≥ R(0).
Las relaciones se simplifican especialmente en el caso de una epidemia en la que se parte de un número muy pequeño de infectados y el resto de la población inicial es susceptible: S(0) ≅ 1, I(0) ≪ 1, R(0) ≅ 0. En tal situación, las ecuaciones tienden a la siguiente forma:
I(t) ≅ 1 − e−R0 R(t) − R(t);
S(t) ≅ e−R0 R(t).
Las siguientes curvas ilustran esta solución simplificada:
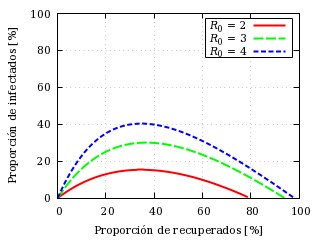
Infectados frente a recuperados.
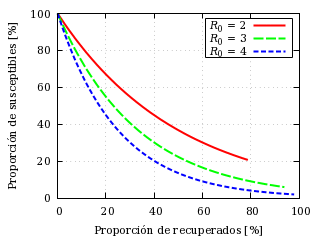
Susceptibles frente a recuperados.
Categorías: Matemáticas, Salud
Permalink: https://sgcg.es/articulos/2020/03/20/el-modelo-epidemiologico-sir-4/
