Mayo de 2010
Calendario de artículos de de 2010
| lu | ma | mi | ju | vi | sá | do |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 |
Día Mundial sin Tabaco
2010-05-31
El Día Mundial sin Tabaco se celebra anualmente el día 31 de mayo. El objetivo es llamar la atención sobre los peligros del tabaco, ese veneno extrañamente popular que los jardineros usan para matar insectos, los anguleros usan para matar angulas y la industria tabacalera usa para matar a sus clientes. Recordemos que, según la Organización Mundial de la Salud, el consumo de tabaco es la segunda causa principal de mortalidad en el mundo. El Día Mundial sin Tabaco tiene un tema nuevo cada año. El tema elegido esta vez es «el sexo y el tabaco con énfasis en la mercadotecnia orientada a las mujeres». En muchos lugares del mundo, las mujeres constituyen un jugoso mercado infraexplotado para una industria tabacalera que vende sus productos a compradoras desprevenidas como una envenenada forma de liberación. Según indica la OMS, alrededor de uno de cada cinco fumadores es mujer. Ahora bien, el consumo de tabaco se reduce lentamente entre los hombres de algunos países, mientras que aumenta en las mujeres. Como una nube de humo arrastrada por el viento, el tabaquismo cambia de posición. Las mujeres embarazadas son especialmente vulnerables, ya que el tabaco no sólo las envenena a ellas, sino que también lo hace con sus futuros hijos en gestación.
Permalink: https://sgcg.es/articulos/2010/05/31/dia-mundial-sin-tabaco/
Día de la Toalla
2010-05-25

Hoy es 25 de mayo, Día de la Toalla.
La toalla es lo más masivamente útil que puede uno llevar encima. Este día 25 de mayo, incauto lector, no olvides llevar una toalla contigo allá donde vayas.
El día de la Toalla es un homenaje a la obra del notablemente notable Douglas Adams.
¡QUE NO CUNDA EL PÁNICO!
Categorías: Fechas
Permalink: https://sgcg.es/articulos/2010/05/25/dia-de-la-toalla/
Principio de Arquímedes
2010-05-20
El principio de Arquímedes es una ley que rige la flotación en un fluido estático. El nombre viene del sabio Arquímedes de Siracusa. El principio es muy fácil de explicar en palabras:
Un cuerpo sumergido experimenta una fuerza de flotación igual al peso del fluido desplazado.
Un cuerpo queda suspendido en un fluido estático cuando su peso es igual al peso del fluido desplazado por su volumen sumergido. Este resultado tan sencillo explica por qué los barcos flotan en el agua y por qué los globos aerostáticos flotan en el aire.
El principio de Arquímedes se aplica a cuerpos sumergidos en fluidos estáticos. Un fluido estático sometido a su propio peso sólo puede mantenerse estático mediante esfuerzos de presión (la presión hidrostática). La presión hidrostática aplicada en el contorno de cualquier volumen del fluido compensa exactamente el peso de dicho volumen de fluido. Si sumergimos un cuerpo en el fluido y logramos que se mantenga quieto de alguna manera, la presión hidrostática será la misma y ejercerá sobre el cuerpo una fuerza de flotación que compensará exactamente el peso que tenía el volumen de fluido que ahora ocupa la parte sumergida del cuerpo.
Podemos hacer una demostración formal del principio de Arquímedes. Para ello, sólo tenemos que aplicar un resultado sencillo del cálculo vectorial y recordar que el gradiente de presión hidrostática ∇p es igual a la fuerza gravitatoria por unidad de volumen ρ g, donde ρ es la densidad del fluido y g es el vector de aceleración gravitatoria. La fuerza F de flotación es el resultado de la aplicación de la presión por toda la superficie sumergida del fluido:
F = ∫∫−p n dS
En la anterior expresión, n es la normal a la superficie sumergida orientada hacia el fluido y dS es un elemento diferencial de superficie sumergida. En virtud del teorema de la divergencia, podemos convertir la anterior integral de superficie por toda la superficie sumergida en una integral de volumen por todo el volumen sumergido. Si el elemento diferencial de volumen es dV, la fuerza de flotación es:
F = ∫∫∫−∇p dV
Hemos visto que el gradiente de la presión es igual al peso del fluido por unidad de volumen. En este caso, este fluido es ficticio, el que ocuparía el volumen sumergido si el cuerpo estuviera ausente. Si aplicamos la igualdad del gradiente de presión y el peso del fluido, la expresión de la fuerza de flotación adopta su forma final:
F = −∫∫∫ρ g dV
Es decir, la fuerza de flotación compensa exactamente el peso del fluido que ocuparía el volumen sumergido del cuerpo si éste no estuviera presente.
Cuando el cuerpo sumergido se desplaza dentro del fluido, el principio de Arquímedes deja de ser aplicable en general. Los esfuerzos en la superficie de contacto del fluido y el cuerpo pueden ser muy distintos de los del caso estático. A pesar de esto, hay muchas situaciones de interés práctico (por ejemplo, si estamos diseñando un dirigible) en las que es posible estimar la fuerza de flotación mediante el principio de Arquímedes y las demás fuerzas fluidodinámicas suponiendo un fluido sin peso, todo ello con un nivel de precisión más que aceptable.
Categorías: Física
Permalink: https://sgcg.es/articulos/2010/05/20/principio-de-arquimedes/
Día de Hablar como un Piloto
2010-05-19
¡Tally-ho! Hoy es el cuarto Día Internacional de Hablar como un Piloto. Recuerda el alfabeto fonético y vigila tus seis.
Categorías: Aeroespacio, Fechas
Permalink: https://sgcg.es/articulos/2010/05/19/dia-de-hablar-como-un-piloto/
Pececito de labios gruesos
2010-05-17

Imagen PNG en 256 tonos de gris, 800 píxeles de ancho y 482
píxeles de alto, 32,3 kB.
Hoy leí un articulito sobre una población de pececillos de labios gruesos que podría encontrarse en el comienzo de un proceso de especiación (enlace a un artículo divulgativo en inglés). La fotografía que acompañaba al texto mostraba un pez de aspecto tan notablemente notable que se hizo poco menos que obligatorio hacer un dibujo del animalito. Los incautos lectores interesados pueden echarle un vistazo al artículo original (en inglés y open access).
Categorías: Dibujos
Permalink: https://sgcg.es/articulos/2010/05/17/pececito-de-labios-gruesos/
Otro gatito
2010-05-15
Hoy parece un día excelente para dibujar gatitos. Aquí tenéis uno:

Imagen PNG en 256 tonos de gris, 800 píxeles de ancho y 1306
píxeles de alto, 63,9 kB.
Categorías: Dibujos
Permalink: https://sgcg.es/articulos/2010/05/15/otro-gatito/
Robot con un regalo
2010-05-14

Imagen PNG en 256 tonos de gris, 800 píxeles de ancho y 1123 píxeles de
alto, 48,5 kB.
Un robotito con un regalo. También hay una versión en color:

Imagen PNG en color, 800 píxeles de ancho y 914 píxeles de
alto, 41,8 kB.
Categorías: Dibujos
Permalink: https://sgcg.es/articulos/2010/05/14/robot-con-un-regalo/
Uso y abuso de las unidades de medida (o por qué un kilómetro y un kilómetro por hora son dos cosas distintas)
2010-05-13
A menudo, es necesario acompañar un nombre de complementos para dar precisión y eliminar la ambigüedad en el lenguaje. Por ejemplo, si queremos indicar cuál es nuestro coche, el único de color rojo que hay dentro de un garaje, podemos referirnos a él como «el coche rojo». Más adelante, cuando nuestro interlocutor ya dispone de un contexto suficiente, podemos omitir la información del color: «voy a echarle un vistazo al coche». Sin embargo, hay casos en los que lo que parece a simple vista un complemento prescindible es en realidad una parte fundamental de lo que efectivamente es un nombre compuesto. Por ejemplo, el martín pescador, un ave que vive en lagos y ríos, no es un tipo especial de «martín». De igual manera, la carabela portuguesa, un organismo colonial marino, no es un tipo especial de «carabela», un tipo de embarcación.
Las unidades de medida sirven para identificar magnitudes físicas. Si dos cantidades tienen unidades diferentes, entonces son cualitativamente diferentes. Está claro que no es lo mismo una longitud que una presión; la siguiente oración es evidentemente absurda: «la distancia de mi casa al trabajo es de cincuenta pascales". Algunas unidades de medida están expresadas mediante varias palabras; por ejemplo, es frecuente usar el metro cuadrado para referirse a la superficie en planta de una casa. Podemos decir: «esta casa tiene una superficie en planta de cincuenta metros cuadrados». También podemos ser un poquito más económicos y hablar de «una casa de cincuenta metros cuadrados» si está claro que nos referimos a la superficie en planta. Lo que es una barbaridad es decir: «esta casa tiene cincuenta metros». ¿Acaso nos referimos al perímetro o a la longitud del pasillo? ¡Evidentemente, no hablamos de la superficie! Un metro cuadrado no es una clase especial de metro, sino una cosa completamente diferente. Si hablamos de lo rápido que se desplazaba un automóvil, podemos decir que «iba a cincuenta kilómetros por hora», pero es una tremenda incorrección decir que «iba a cincuenta kilómetros». Un kilómetro por hora no es una clase especial de kilómetro, sino una cosa completamente distinta. Si usamos las unidades de medida de forma incorrecta, bien podemos ser más atrevidos y económicos: «el coche iba a cincuenta metros» (tan incorrecto como decir que «iba a cincuenta kilómetros», pero más corto), «el coche iba a cincuenta gramos» (el gramo y el kilómetro por hora son igual de diferentes del kilómetro por hora) o incluso «el coche iba a cincuenta» (¿kilómetros por hora, millas por hora…?).
Categorías: Física, Lingüística
Pulseritas mágicas
2010-05-12
Se han puesto de moda unas pulseras que se supone que tienen unos fenomenales efectos sobre la salud y el rendimiento deportivo de quien las lleva. El mecanismo por el que se supone que actúan es una hilarante confusión en la que entran hologramas mágicos y frecuencias misteriosas. Tal mecanismo no tiene fundamento real. Sin embargo, no puedo decir que las pulseritas mágicas son completamente ineficaces. En efecto, el poder de autosugestión es tan grande que, por mera fuerza de creer en saludables frecuencias encerradas en hologramas, una persona puede sentirse mejor y tener mejor rendimiento. Sin embargo, esta persona ingenua podría extraer más utilidad de sus recursos económicos y evitar mantener la industria de los vendedores de aceite de serpiente si reconociera que esas buenas sensaciones y ese buen rendimiento siempre estuvieron dentro de sus capacidades.
La proliferación de productos engañosos y el éxito de la cháchara pseudocientífica que sirve para venderlos pueden ser indicativos de graves deficiencias en la cultura científica y el escepticismo o de una fuerte apatía hacia estos asuntos (quizá los falsos poderes de las pulseritas no entran en consideración y su popularidad sólo se alimenta de sí misma).
Categorías: Miscelánea
Permalink: https://sgcg.es/articulos/2010/05/12/pulseritas-magicas/
Radioaltímetro
2010-05-11
Ayer tuvimos un pequeño contacto con el altímetro barométrico. Hoy vamos a ver otro tipo de altímetro: el radioaltímetro, un ingenioso instrumento que sirve para medir la altura, no la altitud.
El principio básico de funcionamiento del radioaltímetro es muy sencillo: un sistema radar emite una señal radioeléctrica al suelo y determina de alguna manera cuánto tiempo tarda en volver la señal rebotada; este tiempo multiplicado por la rapidez de propagación de la señal da una buena aproximación del doble de la distancia al suelo. En efecto, si suponemos que la señal se propaga en línea recta vertical desde el radar hasta el suelo y desde el suelo hasta el radar, el camino recorrido será el doble de la altura. Si c es la rapidez de propagación de la señal y h es la distancia al suelo, la señal tarda un tiempo Δt ⁄ 2 = h ⁄ c en llegar al suelo y otro tanto tiempo en volver, lo que da un tiempo total Δt = 2 h ⁄ c, de lo que se deduce que la altura es h = c Δt ⁄ 2.
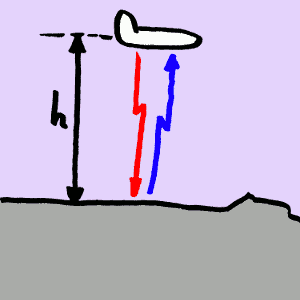
El avión de la figura emite una señal de radar (flecha roja) que
recorre una distancia h hasta el
suelo, rebota y vuelve hacia el avión (flecha azul) recorriendo una
distancia h. La distancia total
recorrida es 2 h.
Hay dos tipos principales de radioaltímetro: el de pulsos y el de frecuencia modulada.
Radioaltímetro de pulsos
Es el tipo de radioaltímetro más sencillo. La señal emitida es un pulso aislado. Es muy fácil emitir este pulso y contar el tiempo que tarda en llegar rebotado.
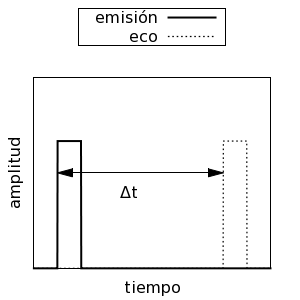
El radioaltímetro de pulsos mide el tiempo transcurrido entre la
emisión de un pulso y la recepción del eco correspondiente.
Radioaltímetro de frecuencia modulada
El radioaltímetro de frecuencia modulada es más preciso que el de pulsos y es más común. La señal va en forma de onda continua modulada en frecuencia. En el planteamiento básico, la señal moduladora es triangular. Si la altura del triángulo de la señal moduladora es Δf y la base (el periodo) es T, la señal rebotada, tras el tiempo Δt que tarda la señal en llegar a tierra y volver, tendra una frecuencia moduladora diferente de la de la señal emitida en ese momento igual a Δf = 2 ΔF Δt ⁄ T. La distancia al suelo será, por lo tanto, h = c T Δf ⁄ (4 ΔF).
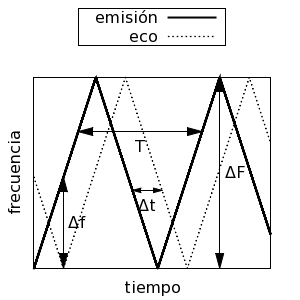
El radioaltímetro de frecuencia modulada funciona midiendo la
diferencia de la frecuencia de la señal original y la frecuencia de la
señal rebotada.
Categorías: Aeroespacio
Permalink: https://sgcg.es/articulos/2010/05/11/radioaltimetro/
Altímetro barométrico
2010-05-10
El espacio aéreo es muy grande y carece de referencias visuales evidentes. Para no perderse en tan vasto espacio, las aeronaves cuentan con instrumentos de navegación de todo tipo. Uno de estos instrumentos es el altímetro, un aparato que determina la altitud de vuelo.
Los altímetros más comunes son los altímetros barométricos. Su principio de funcionamiento es muy sencillo: la medida de presión de la toma de estática entra en un modelo de atmósfera (la Atmósfera Estándar Internacional) que relaciona la presión con la altitud; de ahí se extrae la altitud de vuelo. Este sistema tiene cierta imprecisión porque la atmósfera nunca se comporta como el modelo, pero es a todos los efectos lo bastante bueno y robusto.
Los altímetros barométricos incorporan mecanismos de ajuste que permiten copar en cierta medida con las condiciones meteorológicas específicas. Es posible fijar el reglaje para la presión de referencia. Hay varios reglajes distintos, varios de ellos basados en medidas tomadas en estaciones de referencia que suelen estar en los mismos aeródromos. Estos reglajes toman los nombres de los códigos de comunicaciones por radio que llevan asociados:
- QNH
- Es la presión al nivel del mar que se deduce con el modelo de Atmósfera Estándar Internacional a partir de la medida de presión en la estación de referencia. El reglaje QNH supone que la temperatura a nivel del mar es de 288,15 K, así que pierde precisión cuando la temperatura es distinta.
- QFE
- Es la presión medida en un punto de referencia. La altitud se mide relativa a este punto. Por ejemplo, si se toma la referencia QFE de un aeródromo, un avión tendrá altitud nula (aproximadamente) cuando se encuentre en tierra en ese mismo aeródromo.
- QNE
- Es la presión estándar al nivel del mar del modelo de Atmósfera Estándar Internacional. Cuando los aviones vuelan alto y lejos de los aeródromos de origen y destino, no hay ganancia significativa en usar el reglaje QNH, así que se usa el QNE, de modo que todos los aviones en ruta tienen la misma referencia.
- QFF
- Es la presión al nivel del mar deducida a partir de la presión y la temperatura medidas en la estación de referencia. Los demás parámetros (incluyendo el gradiente térmico) son los de la Atmósfera Estándar Internacional.
Varias de las anteriores referencias de presión se basan en reducir al nivel del mar la presión tomada en una estación de medida. Esta reducción se hace mediante el modelo de Atmósfera Estándar Internacional dejando como variable a calcular la presión al nivel del mar (y la temperatura al nivel del mar en el reglaje QFF). Como la altitud de la estación de medida se conoce con buena precisión, estas reducciones son de buena calidad, o por lo menos son tan buenas como el modelo de comportamiento de la atmósfera.
Categorías: Aeroespacio
Permalink: https://sgcg.es/articulos/2010/05/10/altimetro-barometrico/
Atmósfera Estándar Internacional
2010-05-09
La Atmósfera Estándar Internacional (conocida por sus siglas en inglés, ISA, de International Standard Atmosphere) es un modelo matemático sencillo que sirve para estimar las propiedades atmosféricas en función de la altitud.
El modelo ISA viene a representar la atmósfera típica de las latitudes medias. La atmósfera real nunca se comporta exactamente como la Atmósfera Estándar Internacional, pero sí se parece lo bastante como para que el modelo sea útil en muchas ocasiones, tales como el diseño de vehículos aéreos y la altimetría barométrica. En estos casos, el uso de un modelo atmosférico estandarizado es evidentemente ventajoso, pues en todo caso hace falta un modelo matemático del comportamiento de la atmósfera para cometer tales labores y, si no hay un modelo de referencia reconocido por toda la comunidad aeronáutica, no es posible comparar los méritos de diferentes diseños de forma fiable y la altimetría barométrica se vuelve inútil.
El estándar ISO 2533:1975 recoge la Atmósfera Estándar Internacional y OACI tiene un modelo atmosférico casi idéntico, la Atmósfera Estándar de OACI (ICAO Standard Atmosphere). ¡Estos estándares son costosos de adquirir para el individuo!
El modelo supone que la atmósfera es un gas ideal que se encuentra en equilibrio hidrostático en presencia de un campo gravitatorio uniforme de valor absoluto g. La referencia de altitud h = 0 es el nivel del mar. Las tres propiedades más significativas de la atmósfera (la presión p, la densidad &rho y temperatura T) están ligadas con la altitud h por un sistema de tres ecuaciones. La primera de estas ecuaciones es la de estado del gas ideal:
p = ρ R T
La segunda ecuación es la ecuación diferencial del equilibrio hidrostático:
dp ⁄ dh + g ρ = 0
La tercera ecuación liga la temperatura con la altitud. La atmósfera está dividida en varias capas. En cada capa, la temperatura puede ser constante o puede variar linealmente con la altitud. En aras de la simplicidad, sólo vamos a ver lo que pasa en la troposfera (hasta la tropopausa ht = 11 km) y la región inferior de la estratosfera (encima de la tropopausa). La temperatura desciende linealmente con la altitud en la troposfera y se mantiene constante en la región inferior de la estratosfera:
T(h ≤ ht) = T(0) + (dT ⁄ dh) h
T(h > ht) = T(ht)
Podemos despejar la presión:
p(h ≤ ht) = p(0) (1 + (dT ⁄ dh) (h ⁄ T(0)))−g ⁄ (R dT ⁄ dh)
p(h > ht) = p(ht) e−g (h − ht) ⁄ (R T(ht))
También podemos despejar la densidad:
ρ(h ≤ ht) = ρ(0) (1 + (dT ⁄ dh) (h ⁄ T(0)))−g ⁄ (R dT ⁄ dh) − 1
ρ(h > ht) = ρ(ht) e−g (h − ht) ⁄ (R T(ht))
Para darle sentido al modelo, hace falta que las constantes tengan valores. Estos valores son:
- R = 287,05 J kg−1 K−1
- g = 9,80665 m s−1
- dT ⁄ dh = −6,5 K km−1
- ht = 11 km
- T(0) = 288,15 K
- p(0) = 101,325 kPa
- ρ(0) = 1,2250 kg m−3
La siguiente gráfica muestra las propiedades del aire en función de la altitud según la Atmósfera Estándar Internacional:
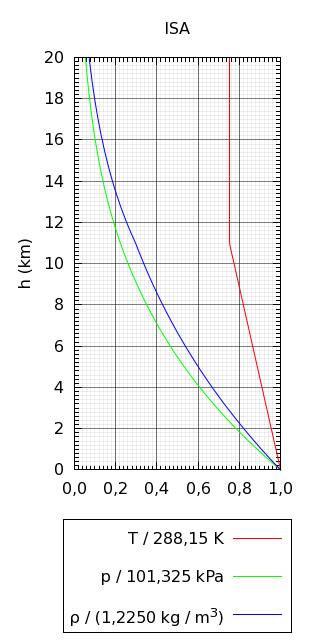
Temperatura, presión y densidad del aire para las capas bajas de la
Atmósfera Estándar Internacional.
La temperatura de referencia básica es T(0) = 288,15 K. El modelo se adapta fácilmente a días cálidos y fríos simplemente con variar esta temperatura básica dejando constante el valor de la presión de referencia p(0) = 101,325 kPa y calculando el nuevo valor de la densidad de referencia ρ(0) mediante la ecuación de estado del gas ideal. La presión a nivel del mar p(0). Como el gradiente térmico dT ⁄ dh no varía, la temperatura T(ht) en la tropopausa cambia tanto como la temperatura T(0) al nivel del mar.
En la Wikipedia en inglés hay un interesante artículo (editado el 7 de abril de 2010 a las 23:46) con enlaces de gran utilidad.
Categorías: Aeroespacio
Permalink: https://sgcg.es/articulos/2010/05/09/atmosfera-estandar-internacional/
Día de Cuidar el Jardín Desnudo
2010-05-08
Hoy es el Día Mundial de Cuidar el Jardín Desnudo o Día Mundial de la Jardinería al Desnudo. Se anima a la gente de todo el mundo a practicar la jardinería sin ropa. Es una forma excelente de reencontrarse con la naturaleza y con uno mismo.
El Día de la Jardinería al Desnudo se celebra el primer sábado de mayo. No hay problema si el jardín es modesto: plantar un geranio au naturel vale.
Categorías: Fechas
Permalink: https://sgcg.es/articulos/2010/05/08/dia-de-cuidar-el-jardin-desnudo/
Día sin Pantalones
2010-05-07
El primer viernes de mayo es el Día sin Pantalones. Para participar en las celebraciones de tan notabilísimo día, sólo hay que quitarse (o no ponerse) los pantalones y dejar al aire las piernas y la ropa interior.

Unos pantalones de deporte en pleno vuelo parabólico.
¡No vale hacer trampas! Las faldas, los vestidos y otros sustitutos de los pantalones están «prohibidos».

Los pantalones se alejan, se alejan…
Dicen que el Día sin Pantalones podría remontarse a 1985. Ha pasado suficiente tiempo desde entonces como para que la fiesta haya sido transmitida de padres a hijos. Existe una cierta probabilidad de que nos encontremos ante una tradición en toda regla.
Categorías: Fechas
Permalink: https://sgcg.es/articulos/2010/05/07/dia-sin-pantalones/
Altura frente a altitud
2010-05-05
En el uso cotidiano, las palabras «altura» y «altitud» vienen a designar lo mismo: una dimensión vertical, bien frente a un nivel de referencia, bien la propia dimensión vertical de un cuerpo. El uso aeronáutico, por otra parte, mantiene una sutil diferencia entre las dos palabras cuando se hace referencia a la posición vertical de un cuerpo:
- Altura
- Posición vertical referida al suelo situado justo bajo el cuerpo.
- Altitud
- Posición vertical referida a un nivel de referencia fijo (el nivel del mar, típicamente).
La altura depende de las características orográficas locales. Un avión puede volar a una altitud fija sobre el nivel del mar pero con altura muy variable al pasar por encima de valles y montañas.
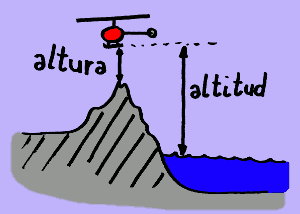
El helicóptero del dibujo se encuentra a gran altitud (sobre el nivel del
mar) pero a baja altura (sobre las montañas).
En otras jergas técnicas, la altitud está definida de forma semejante. Es muy recomendable hacer la distinción entre «altitud» y «altura» para evitar ambigüedades.
Categorías: Aeroespacio, Lingüística
Permalink: https://sgcg.es/articulos/2010/05/05/altura-frente-a-altitud/
Día contra el DRM
2010-05-04
Hoy es el Día contra el DRM. Pronto revisaré el Calendario Festivo Extraoficial para incluir este día y otros que también son muy importantes.
Los sistemas DRM son anticaracterísticas que sirven para impedir que tú, incauto lector, seas dueño de lo que compras. El significado oficial de las siglas «DRM» es Digital Rights Management (gestión digital de derechos), pero esto no es más que una insidiosa maniobra para engañar a la gente, ya que los sistemas DRM no sirven para gestionar los derechos de nadie, sino para restringir y anular los legítimos derechos del usuario; es por ello que muchos preferimos una interpretación alternativa de las siglas más acorde con la realidad: Digital Restrictions Management (gestión digital de restricciones).
El coste del desarrollo y la implantación de un sistema DRM no aumenta la calidad del producto al que se aplica, sino que la reduce y perjudica gravemente al usuario. Es importante que añada algo de énfasis a este hecho escandaloso: los sistemas DRM hacen que haya que pagar más por productos de calidad inferior que perjudican a los usuarios.
Voy a contar una pequeña historia de horror personal sobre un sistema DRM. Hace pocos años, alguien me regaló, en su inocencia, una película en deuvedé. Se trataba de material de importación que parecía no interesar lo suficiente a los distribuidores españoles. Lamentablemente, estas películas vienen con un sistema DRM de «control regional» que sirve para impedir el libre comercio internacional y así imponer una diferenciación artificial de precios. Los reproductores de películas en deuvedé vendidos en España no podían, en principio, mostrar la película que me regalaron, ya que era de una región «extranjera». Tuve que perder mi tiempo para saltarme esta restricción técnica. Una vez superado el primer DRM, me encontré con un segundo sistema que hacía ilegibles grandes partes del contenido para todos los lectores en los que lo probé. Superar esto fue costoso, desagradable e innecesario: la persona que me hizo el regalo fue capaz de conseguir una copia sin DRM por medios alternativos menos queridos por la empresa que le vendió un producto claramente defectuoso.
Quejarse por el DRM de una película puede ser algo frívolo. Quizá pueda parecer menos frívolo si hablamos de libros de texto. Quizá pueda parecer menos frívolo si hablamos de cómo se obliga al público a aceptar que ya no tiene propiedad mientras que una corporación sí la tiene.
Permalink: https://sgcg.es/articulos/2010/05/04/dia-contra-el-drm/
Presión hidrostática
2010-05-04
Hay varias formas de interactuar con un medio. De forma ideal, podemos clasificarlas según su ámbito de actuación. Podemos interactuar con un medio a través de esfuerzos en su superficie y a distancia por todo su volumen. Si aplicamos un esfuerzo sobre una superficie, podemos expresar este esfuerzo como la suma de dos componentes: una componente tangencial a la superficie y una componente normal a la superficie. Los fluidos son sustancias que pueden suportar esfuerzos normales, pero no esfuerzos tangenciales. Si un fluido está quieto, entonces puede que esté soportando esfuerzos normales (presión) distribuidos por su superficie, pero no esfuerzos tangenciales. Para que el fluido se mantenga estático, los esfuerzos normales han de estar en oposición exacta a las fuerzas de largo alcance aplicadas por todo el volumen.
La presión hidrostática es la presión que experimenta un fluido cuando está en condiciones estáticas y sometido a su propio peso. El peso, por supuesto, está orientado según la vertical hacia abajo. Podemos pensar en el fluido como en una torre humana: al igual que el casteller sostiene sobre sus hombros el peso de los compañeros que tiene encima y con sus pies transmite el peso que tiene en los hombros más su propio peso al compañero que tiene debajo, cada partícula fluida soporta en su cara superior la presión que le transmite la partícula fluida que tiene inmediatamente encima de ella y a través de su cara inferior transmite esta presión y su propio peso a la partícula fluida que tiene inmediatamente debajo.
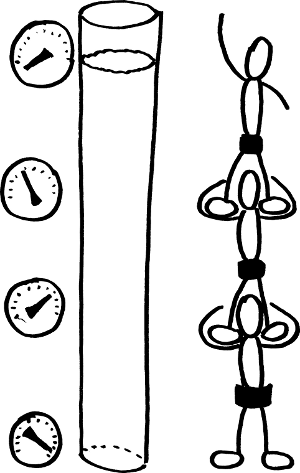
Estos simpáticos castellers dibujados con palitos están
haciendo una demostración de cómo se transmite la presión hidrostática.
Supongamos una minúscula partícula fluida de densidad ρ y forma cúbica de arista l. El volumen de la partícula es l3 y la superficie de cada una de sus caras es l2. La masa de la partícula fluida es, por lo tanto, igual a la densidad multiplicada por el volumen: ρ l3. Si g es la aceleración del campo gravitatorio (positiva hacia abajo), entonces el peso de la partícula fluida, igual a la aceleración gravitatoria multiplicada por la masa, es ρ g l3 (positivo hacia abajo). La presión en la cara inferior es pi (positiva hacia arriba), así que la fuerza que soporta la cara inferior, igual a la presión multiplicada por la superficie, es pi l2 (positiva hacia arriba). De igual manera si la presión en la cara superior es ps (positiva hacia abajo), la fuerza en la cara superior, igual a la presión multiplicada por la superficie, es ps l2 (positiva hacia abajo). Para que la partícula fluida esté quieta, la suma de fuerzas ha de ser nula. Por lo tanto, la hidrostática establece la siguiente relación:
(ps − pi) ⁄ l + ρ g = 0
En el límite de una partícula fluida infinitesimal, la anterior expresión se convierte en una ecuación diferencial:
dp ⁄ dz + ρ g = 0
El símbolo dp ⁄ dz denota la derivada con respecto a la vertical (positiva hacia arriba).
Si podemos suponer que la densidad es constante y el campo gravitatorio es constante (una excelente suposición para muchos casos prácticos con agua), la presión hidrostática es muy fácil de obtener en función de la coordenada vertical z (positiva hacia arriba):
p(z) = −ρ g z + p(0)
En el caso del agua en un gran depósito (¡que puede ser el lecho marino!) con su parte superior destapada y en contacto con la atmósfera, es muy cómodo tomar como referencia vertical el nivel de la superficie libre del agua. La presión p(0) es la presión atmosférica en contacto con la superficie del agua. La densidad del mar es tal que, con muy buena aproximación, un descenso de diez metros supone un incremento de presión de cien kilopascales (un bar). Un reloj sumergible con la leyenda de resistir una presión de 20 bar puede resistir, por lo tanto, estar sumergido 200 m bajo el mar… ¡más o menos (enlace a un artículo de la Wikipedia en inglés con fecha de edición de 16 de abril de 2010 a las 12:25)!

Este reloj podría sobrevivir durante un breve intervalo de tiempo a
200 m de profundidad.
Categorías: Física
Permalink: https://sgcg.es/articulos/2010/05/04/presion-hidrostatica/
Primer aniversario
2010-05-03
SGCG comenzó su andadura el 3 de mayo de 2009. Ha pasado un año como un suspiro desde entonces, un año durante el que he tenido el placer de compartir muchas cosas con los incautos lectores.
Estoy especialmente contento por el proyecto del Calendario Festivo Extraoficial. Gracias a las valiosas contribuciones de personas como tú, incauto lector, el Calendario ha tomado forma y se ha convertido en una parte fundamental de este sitio.
El proyecto de cortometraje Suplente avanza lentamente, pero avanza. Ya está rodado casi por completo. ¡Hay material promocional y todo!
Uno de los artículos más divertidos de preparar del año fue el de la entrega de los Globos de Oro. Escribí este artículo en directo. ¡Poco importó que todos los incautos lectores cinéfilos estaban ocupados viendo las retransmisiones de la ceremonia o durmiendo! Lo bueno que tiene llevar un medio de comunicación sin compromisos económicos es que uno puede permitirse caprichos como éste.
Varios incautos lectores se han convertido en incautos colaboradores… ¡y no se les escapa tema alguno! Han tratado cuestiones tan dispares como la lingüística, las supersticiones y las sutilezas técnicas del patinaje artístico.
Un artículo reciente sobre sobre cómo superar cierta restricción técnica absurda ha resultado ser de gran ayuda para mucha gente. Están llegándome muchos mensajes de correo electrónico de personas agradecidas, personas con dudas y personas con nuevos problemas (¡estoy trabajando en ello, amigos!). Estoy muy contento con el interés generado.
He pasado ratos muy agradables preparando mis dibujitos de chicas guapas y otras monadas. Uno de estos dibujos ha resultado ser la pieza más popular de SGCG: el gatito del 15 de mayo de 2009. Aquí está:

Este gatito tiene
mucho éxito.
¡Buen año, buena cosecha de artículos! Incauto lector, a ti te los dedico. ¡Así sigamos divirtiéndonos e inspirándonos!
Categorías: Miscelánea
Permalink: https://sgcg.es/articulos/2010/05/03/primer-aniversario/
