SGCG

Volver arriba

Tensiones o esfuerzos mecánicos (16)

2016-06-23

La mecánica de los medios continuos se ocupa del estudio del comportamiento macroscópico de los sólidos y los fluidos no como sistemas de partículas sueltas, sino como medios infinitamente divisibles. Se trata de una disciplina que, además de poder ser interesante por sus propios méritos, es la base de buena parte de nuestro actual desarrollo tecnológico. Uno de los conceptos más importantes de la mecánica de los medios continuos es el del tensor de tensiones o esfuerzos, que es una descripción matemática del estado de fuerzas por unidad de superficie en el seno de un medio continuo. Vimos hace unos meses que las tensiones en un medio continuo quedan caracterizadas mediante un tensor simétrico de segundo orden: el tensor de tensiones. Hay varias maneras de resumir las características de este tensor; recientemente echamos un vistazo a la cuádrica directriz de tensiones, que es una representación geométrica del tensor de tensiones que permite conocer algunas propiedades cuando se sabe la dirección del vector tensión. La cuádrica directriz de tensiones es muy similar a la cuádrica indicatriz de tensiones y, como ella, también relaciona relaciona el vector tensión y la dirección normal al plano de medida, pero esta vez en el sentido inverso al permitido por la cuádrica indicatriz de tensiones.

La cuádrica indicatriz de tensiones como herramienta gráfica de cálculo del vector normal

Con la notación del artículo previo, la cuádrica directriz de tensiones es la superficie cuyos puntos (de coordenadas {y₁, y₂, y₃} en en ejes principales) obedecen la ecuación implícita siguiente:

σ ⁄ |σ| = signo(σ) = (x₁)² ⁄ σ₁ + (y₂)² ⁄ σ₂ + (y₃)² ⁄ σ₃.

En un punto cualquiera de la cuádrica directriz de tensiones, el plano tangente es perpendicular a la dirección M (de componentes {M₁, M₂, M₃}) marcada por el gradiente de la ecuación implícita:

M₁ = 2 y₁ ⁄ σ₁ = 2 t₁ ⁄ (σ₁ √|σ|);

M₂ = 2 y₂ ⁄ σ₁ = 2 t₂ ⁄ (σ₂ √|σ|);

M₃ = 2 y₃ ⁄ σ₃ = 2 t₃ ⁄ (σ₃ √|σ|).

Por otra parte, el vector tensión t tiene componentes

t₁ = n₁ σ₁;

t₂ = n₁ σ₂;

t₃ = n₁ σ₃.

Esto es lo mismo que decir que el vector normal al plano de medida tiene componentes

n₁ = t₁ ⁄ σ₁;

n₂ = t₂ ⁄ σ₂;

n₃ = t₁ ⁄ σ₃.

El vector normal al plano de medida y el vector perpendicular a la cuádrica directriz de tensiones son colineales.

Conocida la cuádrica directriz de tensiones, es fácil calcular gráficamente el vector normal para vector tensión dado:

1. se traza desde el origen una línea orientada según el vector tensión que intersecta la cuádrica directriz de tensiones;
2. en este punto de intersección, se traza el plano tangente a la cuádrica;
3. se traza la perpendicular al plano tangente que pasa por el origen;
4. esta perpendicular es colineal con el vector normal al plano de medida;
5. la orientación del vector normal queda determinada con el signo de la tensión normal: si es de tracción, el vector normal tensión apunta hacia el vector tensión; si es de compresión, apunta en sentido opuesto.

La siguiente figura (bidimensional para facilitar la visualización) sirve de ejemplo:

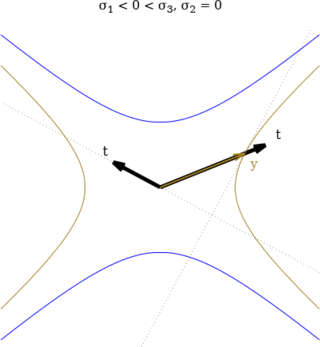
Cálculo gráfico mediante la cuádrica indicatriz de tensiones. Dado un vector tensión t, se calcula el punto correspondiente y en la cuádrica indicatriz sin más que prolongar hasta la intersección. Seguidamente, se traza el plano tangente a la cuádrica (línea de puntos tangente a la rama de hipérbola en el punto y. El vector normal está en la recta que pasa por el origen y es perpendicular a la tangente (la otra línea de puntos). La orientación queda determinada en este caso porque se espera que la tensión normal sea compresiva, es decir, que apunte en sentido opuesto a la dirección normal de medida n.

Categorías: Física

Artículos publicados el mismo mes

Permalink: https://sgcg.es/articulos/2016/06/23/tensiones-o-esfuerzos-mecanicos-16/

Volver arriba