Abril de 2010
Calendario de artículos de de 2010
| lu | ma | mi | ju | vi | sá | do |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | ||
Sistema Pitot-estática
2010-04-30
Si uno mira de cerca un avión, descubre que está lleno de tubitos y otras protuberancias. Cada uno de estos bultos es un dispositivo que cumple una función. Hoy vamos a ver uno de ellos: el sistema de Pitot-estática (que forma parte del sistema de datos de aire). Este sistema sirve para medir la rapidez relativa al viento con la que se mueve un cuerpo (o la rapidez con la que incide el viento sobre un cuerpo). Veamos cómo funciona.
El sistema de Pitot-estática es una combinación de dos sondas distintas. Cada una de estas sondas mide la presión en unas condiciones características; de estas medidas de presión, gracias al Principio de Bernoulli, puede deducirse la rapidez. Una sonda es un tubo de Pitot, mientras que la otra es una sonda de presión estática.

Un humilde tubo de Pitot en el techo de un túnel de viento.
Tubo de Pitot
El tubo de Pitot es un aparato que se usa para medir la presión de remanso de una corriente fluida. La presión de remanso es la presión que alcanza una partícula fluida cuando es frenada suavemente (sin disipación), es decir, al remansar la corriente. El principio de Bernoulli establece cuál es esta presión de remanso. En efecto, si la corriente sin perturbar tiene una densidad ρ∞, una celeridad v∞ y está a una presión p∞ y, además, podemos considerar que el fluido es incompresible, tenemos el siguiente resultado para la presión de remanso pt:
pt = p∞ + ρ∞ (v∞)2 ⁄ 2
El tubo de Pitot no es más que un tubo alineado con la corriente con una embocadura en su extremo de barlovento pero cerrado en el otro extremo. En el interior del tubo hay un sensor de presión. La corriente pasa de estar en movimiento fuera del tubo hasta detenerse en el interior del tubo (se comprueba que la corriente está remansada en el interior del tubo porque si no lo estuviera, entraría más y más fluido hasta hacer que las paredes reventaran). El tubo de Pitot se usa normalmente en fluidos como el aire y el agua en unas condiciones para las que puede remansar la corriente sin disipación, así que la presión que mide el sensor es la de remanso. Si hubiera disipación, la ecuación de Bernoulli no se aplicaría y la presión sería menor que la de remanso.
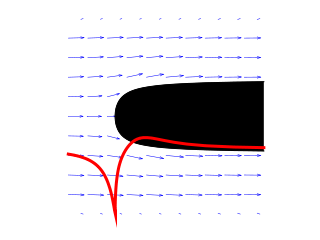
La figura negra es un tubo de Pitot visto de perfil. La
corriente viene desde la izquierda de la imagen. Las flechas
representan el campo de velocidades del viento. La línea roja
representa representa la rapidez de la corriente en el eje del tubo
aguas arriba de la embocadura y en la superficie del tubo aguas
abajo de la embocadura; toca la parte inferior de la imagen en el
punto de remanso y asciende conforme lo hace la rapidez. ¡El incauto
lector avispado notará que este tubo en concreto no está muy bien
diseñado!
Toma de presión estática
La expresión «presión estática» puede resultar engañosa: no se refiere a la presión de la corriente al detenerla (ésa es la presión de remanso), sino a la propia presión que hay en cada punto. La toma de presión estática (o «toma de estática») mide la presión p∞ de la corriente sin perturbar. Esta toma se manifiesta como un agujerito practicado en una pared y comunicado con un sensor de presión. La toma de estática está diseñada de modo que ve la corriente sin perturbar; para lograr esto ha de estar en una pared alejada de la influencia de obstáculos y alineada con la corriente sin perturbar.
Todo junto: cómo se calcula la rapidez aerodinámica
El tubo de Pitot mide la presión de remanso pt y la toma de estática mide la presión estática p∞ de la corriente sin perturbar. Si la corriente puede considerarse incompresible, el principio de Bernoulli nos da una expresión muy sencilla para la rapidez relativa v∞ del viento sobre el tubo o del tubo sobre el viento:
v∞ = √(2 (pt − p∞) ⁄ ρ∞)
Además de la celeridad y su razón frente a la rapidez del sonido (es decir, el número de Mach), el sistema de Pitot-estática tiene más usos. La medida de presión estática permite estimar la altitud (indicada en el altímetro barométrico) y su variación temporal (indicada en el variómetro).
Tubo de Prandtl
El tubo de Prandtl es una sonda que integra en un tubo de Pitot la toma de estática. El tubo ha de ser bastante esbelto y la toma de estática debe estar situada en la parte posterior, donde la corriente ha «olvidado» la presencia de obstáculos.
Categorías: Aeroespacio
Permalink: https://sgcg.es/articulos/2010/04/30/sistema-pitot-estatica/
Día de la Danza
2010-04-29
Hoy, 29 de abril, es el Día de la Danza (en inglés). Este día tiene como objetivo atraer la atención del público, hacer que más gente se interese por el arte de la danza. Hay actos de celebración por todo el mundo que incluyen clases magistrales, actuaciones, artículos y charlas.

El ser humano lleva bailando desde la más nebulosa antigüedad. La danza es una liberación, el más delicioso atrevimiento: el cuerpo se convierte en viento y todos sus recursos son explotados de forma simultánea para crear una belleza continua y fluida que se extiende en el tiempo y el espacio. La danza es emoción e intelecto, es control sobre el caos y descontrol sobre el orden, es la sublimación del movimiento y, ante todo, la danza es divertida.
Permalink: https://sgcg.es/articulos/2010/04/29/dia-de-la-danza/
Rodando unas escenas de exteriores de Suplente
2010-04-27
¡Zombis por todas partes! Este domingo rodamos buena parte de las escenas de exteriores de Suplente.

Una alegre foto de grupo: los zombis posan junto a Harold.
Imagen JPEG en color, 640 píxeles de alto y 480 píxeles de ancho, 106,9 kB.

Una zombi se tambalea detrás de Harold.
Imagen JPEG en color, 640 píxeles de alto y 360 píxeles de ancho,
35,9 kB.

Harold pedalea. ¿Qué le espera más adelante?
Imagen JPEG en color, 640 píxeles de alto y 360 píxeles de ancho,
44,2 kB.

Con la primavera salen las flores y los zombis.
Imagen JPEG en color, 640 píxeles de alto y 360 píxeles de ancho,
67,1 kB.

Dos zombis en el límite de la civilización.
Imagen JPEG en color, 640 píxeles de alto y 360 píxeles de ancho,
61,7 kB.
Categorías: Cine
Permalink: https://sgcg.es/articulos/2010/04/27/rodando-unas-escenas-de-exteriores-de-suplente/
Día de Chernóbil
2010-04-26
Hoy es el Día de Chernóbil, una fecha para recordar el accidente de Chernóbil (enlace a un artículo de la Wikipedia en español con fecha de edición de 18 de abril de 2010 a las 2:14) y reflexionar sobre las terribles consecuencias de un accidente nuclear.
El 26 de abril de 1986, un ensayo de seguridad en el reactor número 4 de la planta de generación de energía de Chernóbil salió catastróficamente mal. Se produjo una gran explosión (en realidad, más de una) que abrió la estructura del edificio. La explosión y el incendio posterior exparcieron por la atmósfera de peligrosísimas cantidades de materia radiactiva. La contaminación afectó, afecta y afectará negativamente a la salud de seres humanos y todos los seres vivos de unos generosos alrededores del lugar del accidente. La heroica actuación de los liquidadores (enlace a un artículo de la Wikipedia en español con fecha de edición de 24 de abril de 2010 a las 17:29), quienes trabajaron poniendo su salud en juego para luchar contra las consecuencias del desastre, permitió minimizar unos daños que, de todos modos, fueron tremendos.
Como suele suceder con toda la actividad industrial humana, los sistemas de generación de energía eléctrica van acompañados de problemas de impacto ecológico. Las centrales nucleares son ahora mucho más seguras que en el pasado, pero el fantasma de Chernóbil sigue presente. Por otro lado, las alternativas prácticas actuales no están libres de efectos perniciosos. El debate sobre la energía nuclear está muy vivo.
Permalink: https://sgcg.es/articulos/2010/04/26/dia-de-chernobil/
Día del ADN
2010-04-25
El 25 de abril de 1953 fue publicado el artículo de Watson y Crick en el que aparecía explicada la estructura de doble hélice del ácido desoxirribonucleico (enlace a un artículo de la Wikipedia en español con fecha de edición de 25 de abril de 2010 a las 8:53), el material del que está hecha nuestra herencia. En recuerdo de tal hito, en muchos lugares del mundo se celebra el Día del ADN. También se celebra la compleción (más o menos) del Proyecto Genoma Humano el mes de abril de 2003. Las celebraciones incluyen numerosas actividades educativas.
Aunque la fecha habitual de celebración es el 25 de abril, este año cayó el 23 de abril, dos días antes de lo normal, en Estados Unidos. En Europa, la celebración es hoy, 25 de abril.
Categorías: Fechas
Permalink: https://sgcg.es/articulos/2010/04/25/dia-del-adn/
Velocidad frente a rapidez
2010-04-24
En español no técnico, las palabras «velocidad», «rapidez» y «celeridad» son efectivamente sinónimas entre sí: en relación con la cinemática de un móvil, significan la magnitud que expresa el espacio recorrido por unidad de tiempo. Las cosas son algo diferentes en la jerga técnica: la velocidad es la magnitud vectorial del desplazamiento (con su dirección) por unidad de tiempo, mientras que la celeridad o rapidez es la magnitud escalar de la distancia recorrida (sin considerar la dirección) por unidad de tiempo. Mantener con rigor esta distinción ayuda a evitar la confusión en discusiones técnicas.
Categorías: Física, Lingüística
Permalink: https://sgcg.es/articulos/2010/04/24/velocidad-frente-a-rapidez/
Actividades libreras del 23 de abril
2010-04-23
La Comunidad de Madrid se viste de bibliófila por una noche. Por quinto año consecutivo, organiza la Noche de los Libros: una noche salpicada de tertulias, conferencias y descuentos en librerías.
Mucho más modesta pero no menos interesante es la Noche de los Libros Mutantes, la respuesta del mundillo independiente al programa oficial. La extensión geográfica es reducida pero bastante apropiada: la actividad se concentra en el rinconcito alternativo de la ciudad de Madrid que es Malasaña.
Actualización:
¡Las actividades no se acaban! Quienes pasen por Lavapiés, pueden
echarle un vistazo a la Plaza Agustín Lara a partir de las 19:00.
Allí podrán participar en el Día del libro y la Cultura
Libre.
Categorías: Madrid
Permalink: https://sgcg.es/articulos/2010/04/23/actividades-libreras-del-23-de-abril/
Principio de Bernoulli
2010-04-18
El principio de Bernoulli es una sencilla relación matemática que relaciona los cambios en la energía cinética, la energía potencial y la presión en un fluido en el que no hay disipación. El principio de Bernoulli para un fluido incompresible (el agua e incluso el aire a baja velocidad se asemejan mucho al modelo de fluido incompresible) y en ausencia de campos de fuerzas (sin gravedad) y en condiciones estacionarias (la distribución de velocidades del fluido por todo el espacio no cambia con el paso del tiempo) tiene el siguiente aspecto:
p + ρ v2 ⁄ 2 = constante
- p ≡ presión;
- ρ ≡ densidad;
- v ≡ rapidez.

Variación de la presión en función de la rapidez para un fluido
incompresible en ausencia de campos de fuerzas.
Esta ecuacioncita algebraica y diminuta tiene un tremendo poder simplificador. En aerodinámica de aviones a baja velocidad, por ejemplo, uno puede obtener casi toda la información que puede desear simplemente resolviendo el sencillo problema cinemático de encontrar cierto campo de velocidades que cumple ciertos criterios sencillos y luego aplicar la anterior ecuación para deducir el campo de presiones del aire.
Si el fluido sigue siendo incompresible y estando en condiciones estacionarias pero ahora hay un campo de fuerzas potenciales, el principio de Bernoulli sigue adoptando una forma muy sencilla:
p + ρ v2 ⁄ 2 + ρ U = constante
U es la energía potencial por unidad de masa. Si no nos movemos mucho, el campo gravitatorio tiene una aceleración de magnitud casi constante g y apunta hacia abajo; su energía potencial por unidad de volumen es U = g z, donde z es la coordenada según la dirección vertical positiva hacia arriba.
Bernoulli dedujo el principio que lleva su nombre sólo para líquidos incompresibles, pero es posible generalizarlo para fluidos compresibles. La forma de la ecuación resultante depende del modelo de comportamiento del fluido. Para un gas ideal, tiene el siguiente aspecto:
v2 ⁄ 2 + a ⁄ (γ − 1) + U = constante
Hay una variable nueva: a, la velocidad del sonido, que suele valer unos 340 m ⁄ s al nivel del mar y es variable como v y U. La constante γ es la relación de calores específicos, una propiedad termodinámica del gas. Para el aire fresquito que hay en capas bajas de la atmósfera terrestre, su valor es aproximadamente igual a 1,4.
Deducción del principio de Bernoulli
Veamos cómo podemos deducir el principio de Bernoulli a partir del primer principio de la termodinámica, el que dice que las variaciones de la energía cinética se deben al trabajo de las fuerzas aplicadas. En aras de una explicación sencilla, sólo vamos a deducir el principio de Bernoulli para un fluido incompresible de densidad uniforme en régimen estacionario en presencia de fuerzas directamente aplicadas que derivan de un potencial. No hay fuerzas disipativas: aparte de las fuerzas que derivan del potencial, sólo actúa la presión.
Vamos a estudiar lo que le pasa a un elemento de fluido, una minúscula cajita fluida de densidad ρ y volumen V. La cara del elemento fluido tiene superficie A y la arista tiene longitud l. El elemento de fluido es infinitesimalmente pequeño. Este elemento de fluido parte de un estado 1 y acaba en un estado 2. Usaremos subíndices numéricos para identificar los estados.
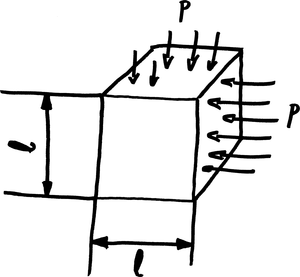
Elemento de fluido sometido a presión constante sobre sus paredes.
Variación de la energía cinética
El incremento de energía cinética es muy fácil de calcular. La energía cinética es la mitad de la masa multiplicada por el cuadrado de la rapidez. El incremento de energía cinética ΔE es:
ΔE = (ρ V ⁄ 2) ((v2)2 − (v1)2)
Trabajo de las fuerzas que derivan de un potencial
Las fuerzas directamente aplicadas son de dos tipos: unas derivan de un potencial (se dice que son conservativas) y las otras se deben a la presión. En primer lugar, calculamos el trabajo de las que derivan de un potencial. Es muy fácil: el trabajo de las fuerzas que derivan de un potencial es igual a la variación de la energía potencial con el signo cambiado. Por lo tanto, el trabajo ΔWc de las fuerzas conservativas es:
ΔWc = ρ V (U1 − U2)
Recordemos que habíamos definido U como la energía potencial por unidad de masa; por eso hemos multiplicado por la masa ρ V del elemento de fluido.
Trabajo de la presión
Esta parte require un poquito de astucia, pero sólo un poquito. El elemento fluido es tan pequeño que la presión inmediatamente alrededor de él puede considerarse constante. Se mueve describiendo una curva, pero supondremos que esta curva es un segmento recto y perpendicular a las caras anterior y posterior del elemento fluido. Esto simplifica las cuentas y los dibujos; el incauto lector puede comprobar fácilmente que el principio sigue siendo válido en el caso general.
Cuando el elemento fluido avanza, la cara anterior barre un camino con la presión dirigida en un sentido. Al avanzar un poco más, la cara posterior va barriendo el mismo camino, pero con la presión dirigida en sentido contrario. El trabajo es la fuerza sobre el camino recorrido, así que lo que la presión en una cara da, la presión en la otra cara lo deshace. Al comienzo del viaje hay un pedacito de camino que sólo barre la cara posterior, mientras que al final del viaje hay un pedacito de camino que sólo barre la cara anterior. Como la distancia recorrida en cada uno de estos pedacitos de camino es muy corta, la presión no varía y su trabajo es igual a la fuerza (el producto de la presión p y la superficie A de la cara del elemento de fluido) multiplicada por la distancia recorrida (igual a la longitud l de la arista del elemento de fluido); el signo de la constribución es positivo para la cara posterior y negativo para la cara anterior porque, si la presión es negativa, su efecto es el de empujar las caras del elemento de fluido. El trabajo ΔWp de la presión se debe a los pedacitos de camino de los extremos 1 (en el que contribuye la cara posterior) y 2 (en el que contribuye la cara anterior) y es:
ΔWp = A l (p1 − p2)

El elemento de fluido se mueve desde la posición 1 hasta la posición 2.
En el volumen rayado, el trabajo que realiza la presión de la cara
posterior anula el trabajo que realiza la presión de la cara anterior.
La presión sólo trabaja en las regiones sin rayar de la posición
1 y la posición 2.
Todo junto
El primer principio de la termodinámica dice que el incremento de la energía cinética es igual al trabajo de las fuerzas exteriores:
ΔE = ΔWc + ΔWp
Si juntamos las expresiones anteriormente deducidas para ΔE, ΔWc y ΔWp, dividimos por la masa ρ V = ρ A l y reorganizamos términos, queda la ecuación de Bernoulli para el fluido incompresible en régimen estacionario en presencian de un campo de fuerzas conservativas:
(v1)2 ⁄ 2 + p1 ⁄ ρ + U1 = (v2)2 ⁄ 2 + p2 ⁄ ρ + U2
Aplicaciones
El principio de Bernoulli tiene una aplicación muy útil: medir la rapidez con la que se mueve un avión en relación al viento. Esto se hace con un tubo de Prandtl que mide la presión estática (la presión del aire sin frenar) y la presión de remanso (es decir, la presión del aire tras frenarlo suavemente hasta que acompaña al avión). La variación de la energía potencial es despreciable. Conocidas las presiones y la celeridad de remanso (que es nula), descubrir la rapidez aerodinámica del avión es sólo cuestión de despejar.
El principio de Bernoulli sirve para explicar cómo funciona un ala a partir de la cinemática del viento alrededor de ella. La forma del ala es tal que la corriente se mueve más deprisa por encima de ella y más despacio por debajo. Por el principio de Bernoulli, la presión es más baja en la cara superior del ala y más alta en la cara inferior; esto da lugar a una fuerza resultante positiva hacia arriba: la fuerza de sustentación.
Categorías: Física
Permalink: https://sgcg.es/articulos/2010/04/19/principio-de-bernoulli/
Primera posición de ballet
2010-04-17

Imagen PNG en 256 tonos de gris, 800 píxeles de ancho y 1631 píxeles de
alto, 53,8 kB.
Existen varias posiciones básicas para los pies y para los brazos en ballet. Aparte de la posición de reposo, hay cinco posiciones básicas para los brazos y otras cinco para los pies. La bailarina del dibujo tiene tanto los pies como los brazos en primera posición.
Hay varios métodos o escuelas de ballet y las posiciones presentan variaciones sutiles y no tan sutiles según el método. Las posiciones descritas en este artículo pueden ser de la escuela francesa o de la escuela rusa.
Primera posición de brazos
Los brazos están curvados con los dedos de ambas manos casi tocándose. Las manos quedan a la altura del ombligo. Los brazos no están ni completamente estirados ni completamente flexionados, sino que forman una figura muy semejante a una circunferencia. Las manos han de continuar con suavidad la curva de los brazos.

Vista en primera persona de un brazo izquierdo en primera posición.
Primera posición de pies
Los pies están completamente apoyados en el suelo, los talones en contacto y las puntas hacia fuera, de modo que los ejes de los pies forman una línea recta. Las piernas están estiradas y en contacto; como están abiertas, se tocan por su parte posterior. Esta posición parte de la cadera: no hay que rotar el pie desde el tobillo, sino la pierna entera desde la articulación de la cadera.
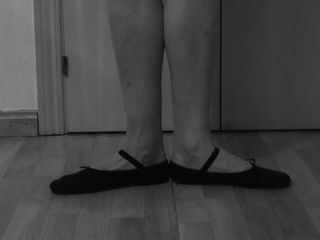
Pies en primera posición.
¡Nadie dijo que el ballet fuera fácil! No es raro encontrar dificultades incluso en la primera posición. Es muy importante mantener en tensión piernas, glúteos, abdomen y espalda. Los pies han de estar abiertos dentro de límites realistas: de nada sirve abrir completamente para caerse un segundo después. El peso ha de estar más concentrado sobre las puntas de los pies que sobre los talones.
Permalink: https://sgcg.es/articulos/2010/04/17/primera-posicion-de-ballet/
Cenizas volcánicas y aviones en tierra
2010-04-15
El glaciar Eyjafjallajökull, situado en Islandia, oculta bajo su helada superficie un volcán activo que entró en erupción recientemente (enlace a un artículo de Wikinews en inglés con fecha de revisión de 15 de abril de 2010 a las 17:33). La nube de ceniza resultante ha provocado fuertes restricciones al tráfico aéreo en el norte de Europa. La página de EUROCONTROL contiene información actualizada sobre la situación.
¿Cómo pueden unas particulitas de ceniza causar tanto alboroto?
Cuando un avión se encuentra con una nube de ceniza volcánica, se producen numerosos fenómenos. Algunos de ellos pueden ser bellos; tal es el caso del fuego de San Telmo y otros fenómenos eléctricos luminosos. Sin embargo, la mayor parte de los fenómenos tiene una naturaleza destructiva y de escaso interés estético.
Una de las consecuencias más significativas del vuelo en una nube de ceniza volcánica es el apagado de los motores. Las partículas de atacan por muchos frentes simultáneamente al motor turbofán de un avión del típico avión de transporte comercial:
- se pegan a los álabes guía del compresor y con ello obstaculizan la entrada de aire;
- bloquean los orificios de refrigeración, lo que provoca un sobrecalentamiento;
- se funden en la cámara de combustión para posteriormente sedimentarse en los álabes de la turbina.
Todo esto forma un mecanismo inestable en el que el motor se aleje del régimen adecuado de operación hasta que se detiene. Una vez se han apagado los motores, el avión desciende en un largo planeo y, si no es posible el reencendido de la planta propulsora, acaba siendo necesario un aterrizaje de emergencia.
La ceniza parece no conformarse con inutilizar los motores y daña el resto del avión. Provoca erosión de superficies, avería de sensores y contaminación de filtros, circuitos neumáticos y de la propia cabina.
La ceniza volcánica no sólo perjudica la seguridad aérea, sino que además lo hace de forma sigilosa. El radar meteorológico de a bordo no puede detectar las pequeñas partículas de ceniza. Los mensajes de información meteorológica contienen avisos y las autoridades aeronáuticas pueden tomar medidas restrictivas como en el presente caso.
Categorías: Actualidad, Aeroespacio
Permalink: https://sgcg.es/articulos/2010/04/15/cenizas-volcanicas-y-aviones-en-tierra/
Noche de Yuri
2010-04-12
El 12 de abril es la Noche de Yuri (Yuri's Night en inglés). Hay fiestas repartidas por todo el globo para celebrar la exploración espacial.
Poco después de las 6:00 UTC del 12 de abril de 1961, un potente lanzador Soyuz salía desde el suelo de Baikonur hacia el firmamento oriental; llevaba consigo la compacta nave Vostok 3KA en cuyo interior se encontraba recogido el cosmonauta soviético Yuri Gagarin. Se trataba de la misión Vostok 1 (Восток-1), el primer vuelo tripulado en llegar al espacio. La astronave alcanzó un apogeo de 315 km de altitud y, tras menos de dos horas de vuelo y una vuelta al mundo a sus espaldas, tocó tierra cerca de las 8:00 UTC. Yuri Gagarin recibió el título de Héroe de la Unión Soviética, la más alta condecoración que se concedía en la URSS. La historia de la misión Vostok 1 está muy bien explicada (¡en inglés!) en un artículo de Encyclopedia Astronautica.
Categorías: Aeroespacio, Fechas, Historia
Permalink: https://sgcg.es/articulos/2010/04/12/noche-de-yuri/
Cambios en el sistema de distribución de vídeos de RTVE
2010-04-10
Actualización:
El sistema de distribución de vídeo de la página de RTVE
ha cambiado varias veces desde la escritura de este artículo y
el método aquí descrito está obsoleto. El método que funciona
en el momento de escribir esta actualización (septiembre de 2012) está
en un artículo más reciente. También hay una versión
al día del programita rtve-mediateca-dl que
implementa esté método.
Hace unas semanas, vimos un método para descargar vídeos de la mediateca de RTVE. Anoche recibí un mensaje en el que un buen ciudadano (un saludo y muchas gracias, A) me avisaba de que el método dejó de funcionar debido a cambios realizados en el sistema de distribución de vídeo. Aun suponiendo que los cambios han sido realizados de forma bienintencionada, la situación es censurable: debemos recordar que los vídeos de RTVE han de ser patrimonio de todos los españoles.
Nuevo programa
Tenemos una nueva versión del programa para descargar vídeos de la
mediateca que es compatible con el nuevo sistema. Los
requisitos son los de siempre: una máquina *NIX con conexión a Internet
y GNU Wget instalado.
He aquí la dirección de descarga del tarball con el código:
rtve-mediateca-dl-2.0.tar.gz.
Para instalar el programa, hay que extraer el contenido del
tarball, echarle un vistazo al Makefile y editarlo
si es necesario y, finalmente, instalar:
make install
El funcionamiento del programa está documentado en una página de
manual:
man rtve-mediateca-dl
También es posible acceder a la ayuda del programa con la opción
--help:
rtve-mediateca-dl --help
Cómo funciona el nuevo método para descargar los ficheros de vídeo
Una pequeña investigación ha permitido descubrir el funcionamiento del nuevo sistema. Algunas cosas siguen como antes; en concreto, el identificador del vídeo que extraíamos del código JavaScript de la página con el reproductor de vídeo incrustado sigue siendo el mismo. Vamos a ver, paso por paso, cómo podemos usar esta información para recuperar la dirección del fichero de vídeo.
- Supongamos que el número identificador es
A1A2A3A4A5A6, donde cada letra con subíndice representa un dígito. Este número aparece en varios lugares como las variable flashcontentId y assetID. - Vigilamos las comunicaciones de nuestro navegador y descubrimos la
descarga del fichero
http://www.rtve.es/swf/data/es/videos/video/A6/A5/A4/A3/A1A2A3A4A5A6.xml. La dirección se construye con los 4 últimos dígitos del número en orden inverso y con separadores de directorio entre dígitos y, finalmente, con el número completo. - Descargamos el fichero XML. Tiene varios elementos, pero el último
es el más interesante. Indica la carga de un complemento llamado
multicdn (cdn como en content delivery
network, red de entrega de contenidos). Tiene un parámetro que
se llama assetDataID cuyo valor es un número de varias
cifras:
B1B2B3B4B5B6. - A partir de aquí, el análisis de la actividad de nuestro
navegador revela poca información la comunicación empieza a estar
ofuscada, pero si nos quedamos un rato mirando fijamente el
complemento de la red de entrega de contenidos, descubrimos muchas
cosas. Resulta que podemos construir la dirección de otro recurso XML
de un modo semejante al anterior, pero esta vez usando el nuevo número
de assetDataID. Esta dirección tiene el siguiente aspecto:
http://www.rtve.es/scd/CONTENTS/ASSET_DATA_VIDEO/B6/B5/B4/B3/ASSET_DATA_VIDEO-B1B2B3B4B5B6.xml. Igual que antes, usamos los cuatro últimos dígitos del número en orden inverso y con separadores de directorio entre ellos y, finalmente, el número completo. - Descargamos el nuevo recurso XML. ¡Está lleno de
información sobre el vídeo que queremos bajar! Rápidamente,
identificamos la presencia de una dirección relativa:
/…/ZZZZZZZZZZZZZ.flv. Aparece dos veces: en un parámetro llamado defaultLocation y en un campo llamado ASD_FILE. - Nos inventamos una dirección que probablemente será la correcta:
añadimos el prefijo
http://www.rtve.esa la dirección que descubrimos en el anterior paso. - Descargamos el contenido de la dirección que acabamos de construir. ¡Tenemos éxito! Queda ver cuánto tiempo pasará hasta que este método deje de funcionar, por supuesto.
Actualización:
El sistema de distribución de vídeo de la página de RTVE
ha cambiado varias veces desde la escritura de este artículo y
el método aquí descrito está obsoleto. El método que funciona
en el momento de escribir esta actualización (septiembre de 2012) está
en un artículo más reciente. También hay una versión
al día del programita rtve-mediateca-dl que
implementa esté método.
Categorías: Informática
Permalink: https://sgcg.es/articulos/2010/04/10/cambios-en-el-sistema-de-distribucion-de-videos-de-rtve/
Ley de los gases ideales
2010-04-08
La ley de los gases ideales es un modelo matemático extremadamente sencillo y útil que sirve para predecir el comportamiento de gases en equilibrio a presiones no muy elevadas. Relaciona la presión, la temperatura y la cantidad de gas presente por unidad de volumen. Las aplicaciones de la ley de los gases ideales son muy amplias y tan dispares como la meteorología, la aerodinámica y la anestesiología. Si la ley de los gases ideales se queda corta, hay modelos más complicados con rangos de validez más amplios.
Podemos deducir la ley de los gases ideales mediante un sencillo experimento mental. Supongamos que tenemos un gas metido en una cajita aislada del mundo exterior. Modelaremos las partículas del gas como pequeñas bolitas elásticas que están colisionando en todo momento contra las paredes de la caja. Miremos de cerca una de las paredes. Las partículas se acercan a la pared, chocan contra ella, rebotan y se alejan de la pared, de modo que cambian la dirección de su cantidad de movimiento.
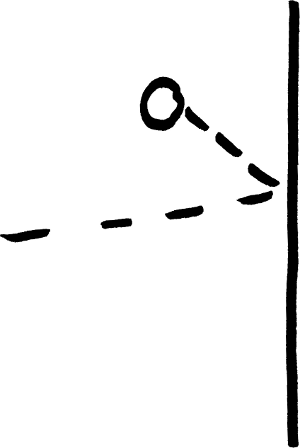
Las partículas rebotan contra las paredes.
Como la cantidad de movimiento del sistema completo ha de mantenerse constante, la pared recibe una cantidad de movimiento que compensa la variación del ímpetu de la partícula que rebota y que en media es proporcional a la celeridad media de las partículas. Dejemos pasar un poco de tiempo. Contra la pared habrán chocado un número de partículas que es evidentemente proporcional al número total de partículas que hay dentro de la caja.
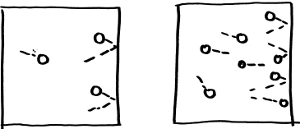
Las colisiones son más frecuentes conforme aumenta el número
de partículas.
El número de colisiones también es proporcional a la rapidez media de las partículas y al tiempo transcurrido.
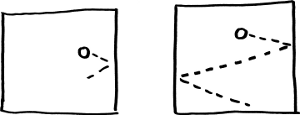
Las partículas tienen más tiempo para chocar contra las paredes
cuando se mueven deprisa y cuando el tiempo transcurrido es largo.
Por último, el número de colisiones es inversamente proporcional a la distancia de pared a pared.
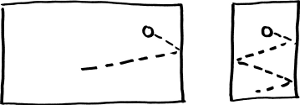
Las partículas tienen más tiempo para chocar contra las paredes
cuando el camino a recorrer es corto.
Cada uno de estos choques aporta un ímpetu a la pared que es en media proporcional a la rapidez media de las partículas, de modo que el ímpetu total que absorbe la pared en un tiempo dado es proporcional al cuadrado de la celeridad media de las partículas, al número de partículas que hay en la caja y al tiempo transcurrido y es inversamente proporcional al tamaño de la caja. La fuerza es la variación de la cantidad de movimiento con el tiempo, así que el ímpetu recibdo por la pared dividido entre el tiempo transcurrido da como resultado la fuerza a la que está sometida la pared. La presión es la fuerza aplicada por unidad de superficie, así que la fuerza a la que está sometida la pared dividida por la superficie de la pared da como resultado la presión a la que está sometida la pared. Esta presión es, por lo tanto, proporcional al cuadrado de la rapidez de las partículas e inversamente proporcional a la distancia de pared a pared y la superficie de la pared. El volumen de la caja crece con el producto de la superficie de la pared y la distancia entre paredes. La energía cinética de las partículas va con el cuadrado de su rapidez, pero lo habitual no es medir la energía cinética, sino una cantidad proporcional a ésta, la temperatura.
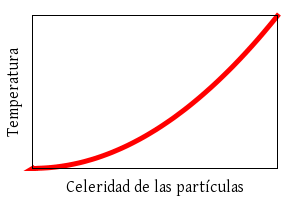
La temperatura y la energía cinética son proporcionales. La
energía cinética es proporcional al cuadrado de la rapidez media de las
partículas.
Si juntamos todo, vemos que la presión es directamente proporcional a
la temperatura y al número de partículas e inversamente proporcional
al volumen de la caja. La forma habitual de escribir esta relación
es la siguiente:
p V = n R T
donde:
- p ≡ presión;
- V ≡ volumen;
- n ≡ cantidad de materia del gas;
- R ≅ 8,314 J mol−1 K−1;
- T ≡ temperatura.
La anterior relación es la ley de los gases ideales.
La ley de los gases ideales combina las leyes empíricas de
Boyle-Mariotte:
p ∝ V−1
(a temperatura constante),
Charles:
V ∝ T
(a presión constante)
y Gay-Lussac:
p ∝ T
(a volumen constante).
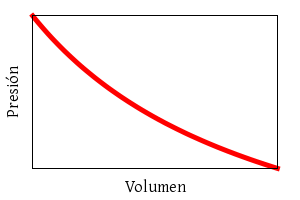
Ley de Boyle-Mariotte.
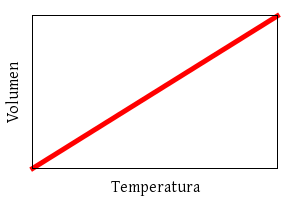
Ley de Charles.
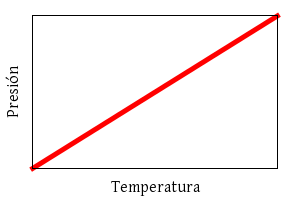
Ley de Gay-Lussac.
Permalink: https://sgcg.es/articulos/2010/04/08/ley-de-los-gases-ideales/
Centenaria Gran Vía
2010-04-05
La Gran Vía tiene un siglo… más o menos. El proyecto fue aprobado a principios del siglo XX y las obras, que comenzaron el mes de abril de 1910, no terminarían hasta décadas después. El nombre de Gran Vía quedó fijado hace unas tres décadas; hasta entonces, los nombres se sucedieron con los intereses políticos de cada momento.

Tráfico rodado en la Gran Vía. A la derecha, el Palacio de la
Música.
La Gran Vía siempre ha estado llena de vida y movimiento. En su momento, era difícil atravesar una puerta y no encontrarse de pronto dentro de un cine o un teatro. Los edificios emblemáticos se suceden para asombrar a los turistas. ¿Qué será de nuestra Gran Vía dentro de cien años?
En la Wikipedia en español hay un bonito artículo general sobre la Gran Vía (enlace a la versión editada el 5 de abril de 2010 a las 11:40) y otro sobre su historia (enlace a la versión editada el 5 de abril de 2010 a las 9:58).
Categorías: Madrid
Permalink: https://sgcg.es/articulos/2010/04/05/centenaria-gran-via/
Sobre cómo la piratería puede impactar negativamente a la producción artística
2010-04-04
La piratería impacta negativamente en la producción artística de nuestro país. La delicada maquinaria del genio artístico se bloquea fácilmente ante la incertidumbre y el fantasma del secuestro durante los largos viajes marítimos. Afortunadamente, la libre participación en la vida cultural debe de estar compensando con creces este efecto, ya que la producción artística nunca había sido tan vibrante como hoy.
Categorías: Miscelánea
Recordemos qué es la piratería
2010-04-03
Sólo quería recordar el significado de la palabra «piratería»:
- Ejercicio de pirata.
- Robo o presa que hace el pirata.
- Robo o destrucción de los bienes de alguien.
Para que queden las cosas bien claritas, recuerdo también el significado del sustantivo «pirata»:
- Persona que, junto con otras de igual condición, se dedica al abordaje de barcos en el mar para robar.
- Persona cruel y despiadada.
Sólo quería recordarlo.
Categorías: Lingüística
Permalink: https://sgcg.es/articulos/2010/04/03/recordemos-que-es-la-pirateria/
Lo sobrenatural en la sociedad tecnológica
2010-04-02
Este artículo surge de una propuesta del incauto lector htg.
Las ideas olvidaron el anticuado concepto de frontera y la ciencia, árida y cargada de fuertes requisitos para ser comprendida, compite contra toda la fantasía del mundo. El sistema de creencias y modelos mentales de una persona elegida al azar puede ser una pintoresca mezcla de sofisticada mecánica y caprichosos espíritus.
La creencia en lo ultraterreno ha acompañado a la humanidad desde siempre. El hombre primitivo, falto de buenos modelos y sobrado de necesidades acuciantes, aceptaba explicaciones inverosímiles e infalsables sobre el funcionamiento del mundo que lo rodeaba. No se distingue mucho el hombre occidental contemporáneo de sus antepasados en este aspecto a pesar de que tiene acceso a grandes avances científicos. No hay que extrañarse por ello. El hombre común puede tener problemas diferentes a los del hombre primitivo, pero sigue teniendo demasiados problemas de los que preocuparse y pocas ganas y tiempo para buscar el auténtico mecanismo del mundo. Dado un fenómeno extraño, la explicación más fácil de asimilar sin necesidad de análisis profundo se impone sin encontrar barrera.
Ante el escrutinio del no iniciado, no hay diferencia entre lo que llamamos «superstición» y lo que llamamos «ciencia»: sólo hay mecanismos cuyo sutil funcionamiento interno nunca es del todo conocido. ¿Existe realmente una diferencia? Al final, uno construye modelos mentales para predecir el funcionamiento del mundo. Estos modelos pueden estar basados en la evidencia empírica y líneas de razonamiento probadas con anterioridad, en cuyo caso los llamamos «ciencia», o pueden estar basados en ideas no meditadas, fantasías agradables y el carismático sermón de terceros, en cuyo caso los llamamos «superstición». Hay que aceptar que no faltará quien simplemente crea explicaciones científicas exactamente igual que como si fueran creencias supersticiosas, sin reflexión ni curiosidad; de igual modo, hay que aceptar que no faltará quien, por falta de conocimientos más profundos, tendrá sin duda un sofisticado modelo mental del mundo basado en conceptos mágicos que se sujetan a falsas o engañosas evidencias empíricas. Para muchos, los ingenios tecnológicos funcionan gracias a misteriosos mecanismos desconocidos y que es mejor no conocer; muchos otros dirigen sus vidas mediante numerosos rituales mágicos de rígidas reglas y basados en una cierta base empírica. Los individuos del último grupo tienen una ciencia que puede ser muy imperfecta por haber sido creada a partir de información muy imperfecta, pero que al fin y al cabo es falsable.
Vemos que la extensión de la superstición en la sociedad occidental contemporánea es algo difícil de evitar y, en cierta medida, un fracaso de la formación científica de la población general. Aparte del factor educativo, si hay otra fuerza motriz detrás de la superstición, ésta es la del dolor que acompaña al ser humano: cuando la ciencia no ofrece consuelo en situaciones injustas e inaceptables (la muerte de un ser querido, por ejemplo), la fantasía acude a ayudar a las mentes abatidas. La fácil circulación de toda clase de información hace más fácil si cabe que las supersticiones se extiendan.
Categorías: Miscelánea
Permalink: https://sgcg.es/articulos/2010/04/02/lo-sobrenatural-en-la-sociedad-tecnologica/
