Junio de 2013
Calendario de artículos de de 2013
| lu | ma | mi | ju | vi | sá | do |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
El polémico patrocinio de la estación de Sol y la línea 2 de Metro de Madrid
2013-06-30
Una empresa dedicada a las telecomunicaciones patrocina la estación de Sol y la línea 2 de Metro de Madrid. El acuerdo incluye cambios de nombre en la estación y la línea para mencionar a la compañía patrocinadora. Estas condiciones no han gustado a unos cuantos madrileños.
- Ecologistas en Acción denuncia la campaña como una de publicidad engañosa por ser encubierta. Ciertamente, los madrileños de hoy tienen pocos motivos para ser engañados, pues la naturaleza publicitaria de los cambios de nombre es muy evidente. Por otra parte, que el público no sea tonto no hace menos fraudulenta la maniobra publicitaria, pues recurre a un cambio de nombre para poder incluir el anuncio de una marca comercial en un espacio supuestamente libre de publicidad comercial como es el cartel que identifica a la estación.
- Ecomovilidad indica que es muy poco dinero el obtenido por el patrocinio. Según indican muchos medios, la campaña le reportará a Metro de Madrid tras tres años unos tres millones de euros. Esto es algo insignificante frente a los 900 millones de euros anuales de déficit de explotación que aparecen en el artículo (identificados como deuda en el propio texto y como déficit de explotación en un comentario) y, además, es notablemente más barato que las tarifas aplicadas por la concesionaria que lleva los carteles publicitarios en las instalaciones de Metro de Madrid.
- Como añadido a lo anterior, la campaña supone un incremento de una décima parte en los ingresos por publicidad de diez millones de euros anuales que tiene Metro de Madrid según señala Business Insider. Esto quizá supone poca actividad en los espacios espacios publicitarios (algo que por otra parte es muy aparente por el número de carteles vacantes que a menudo hay).
- Ha surgido alguna campaña de recogida de firmas contra los cambios de nombre. Aquí hay una sobre Sol.
- Un problema importante que tiene el cambio de nombre de la estación de Sol está en que la marca del patrocinador aparece justo al principio, lo que modifica radicalmente la posición de la estación en el orden alfabético.
La polémica está servida. Metro de Madrid anda mal de dinero, pero el modo de rascar debajo de las piedras para conseguirlo genera cierto disgusto.
Categorías: Actualidad, Madrid
Estimar el tamaño de la Luna a partir de una fotografía
2013-06-29
He aquí un bonito ejercicio educativo: estimar el tamaño de la Luna a partir de una fotografía. Podría estar bien como ejercicio de campo para un escolar: practicaría con una cámara fotográfica y aplicaría unos pocos conocimientos elementales de astronomía, mecánica orbital, óptica y geometría euclídea.
El ejercicio propuesto en este artículo continúa sobre los cálculos hechos en el artículo ¿Está muy lejos la Luna? en el que hacíamos una estimación de la distancia entre la Tierra y la Luna. Hecho el cálculo o admitida la distancia como dato, lo siguiente que hay que hacer es salir de noche a fotografiar la Luna. Para que el ejercicio salga bien, es importante conocer la distancia focal y el tamaño de la película o del sensor con el que se hace la fotografía. Después, hay que medir la Luna en la imagen y hacer unas pocas cuentas. Como ejemplo de aplicación, trabajamos con una fotografía tomada hace un par de años con una cámara réflex digital.

Fotografía de la Luna. Es un recorte reducido de una imagen de
mayor tamaño.
Sabemos lo siguiente:
- La Luna aparece en la fotografía con un diámetro de unos 444 píxeles.
- La distancia focal con la que se tomó la fotografía es de 270 mm.
- El sensor de la cámara tiene 4288 píxeles de ancho.
- El sensor de la cámara mide 23,6 mm de ancho.
- La distancia a la Luna es de unos 0,38 Gm.
- La Tierra tiene un radio de unos 6,4 Mm.
Podemos resolver el problema de determinación del tamaño de la Luna con ayuda del siguiente gráfico ilustrativo:
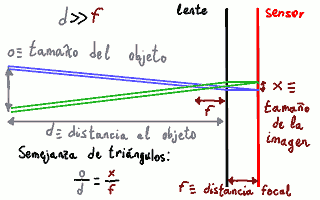
Esquema de la estimación del tamaño de la Luna mediante
trazado de rayos.
El problema queda resuelto sin más que aplicar la razón de semejanza de triángulos del dibujo. También podemos ir paso a paso y dar una interpretación geométrica a cada resultado intermedio. El diámetro x de la Luna ocupa en el plano de la imagen unos 23,6 mm ⋅ 444 ⁄ 4288 ≈ 2,44 mm. Por otra parte, como la Luna está muy lejos (a más de mil millones de veces la distancia focal), podemos asumir que la lente enfoca al infinito. Cuando esto sucede, los ángulos son muy, muy pequeños y podemos aproximar el ángulo cubierto como la razón del tamaño de la imagen x y la distancia focal f: x ⁄ f. En este caso, el ángulo es aproximadamente igual a 2,44 mm ⁄ 270 ≈ 9,04 mrad. La distancia de la superficie terrestre al centro de la Luna es la que separa el centro de la Tierra con el centro de la Luna (los 0,38 Gm) menos el radio terrestre (unos 6,4 Mm), lo que da unos 0,37 Gm, pero como el cálculo que hicimos de la distancia a la Luna no tiene más precisión que dos cifras, realmente no tiene mucho sentido distinguir entre 0,38 Gm y 0,37 Gm. La distancia d = 0,38 Gm multiplicada por el diámetro angular x ⁄ f = 9,04 mrad que tiene la Luna dan un diámetro o de unos 3,4 Mm; el radio es de unos 1,7 Mm. Esto es precisamente el tamaño conocido de la Luna hasta dos cifras significativas, lo que está muy bien.
Categorías: Física
Permalink: https://sgcg.es/articulos/2013/06/29/estimar-el-tamano-de-la-luna-a-partir-de-una-fotografia/
Simpáticas pintadas en la acera bici en Aluche
2013-06-26
Recientemente, aparecieron unas simpáticas pintadas en la acera bici del parque de Aluche que conecta la plaza de la estación con la Casa de Campo.

La primera pintada anuncia el comienzo del nivel 1. La tipografía
recuerda a la que podía encontrarse en un videojuego de los años
ochenta.

Avanzamos y encontramos frutas pixeladas.

Hay frutas de diferentes tipos.

Conforme avanzamos, el juego parece complicarse con la aparición
de graciosas bombitas redondas. Podemos suponer que hay que
esquivarlas y hay que pasar por encima de las frutas.
En efecto, las pintadas parecen un videojuego. Las pintadas muestran indicadores de comienzo de nivel, frutas y bombitas redondas. Conforme avanzan los niveles, la complejidad aumenta. No hay reglas escritas en el suelo, pero podemos inventarnos unas en las que hay que pasar por encima de las frutas y esquivar las bombas. De esta manera, la disposición de las pintadas anima a dar bandazos, lo que es algo peligroso.
Categorías: Madrid
Permalink: https://sgcg.es/articulos/2013/06/26/simpaticas-pintadas-en-la-acera-bici-en-aluche/
Solsticio de junio
2013-06-21
El solsticio de junio de este año cae en día 21. El momento ha ocurrido a las 05:04 UTC (07:04 CEST). En las zonas templadas del hemisferio norte, el veranito llega con algo de timidez. El Sol empieza a acostarse más tarde en el sur, mientras que en el norte se volverá más perezoso.
Categorías: Fechas
Permalink: https://sgcg.es/articulos/2013/06/21/solsticio-de-junio/
Stratasys compra MakerBot
2013-06-20
Hoy ha salido el anuncio de que MakerBot va a ser adquirida por Stratasys. Esto tiene su cosilla. Stratasys es un fabricante bien asentado de máquinas de fabricación aditiva («impresión 3D»… ¡pero esta expresión es algo horrible!). MakerBot es una compañía más joven que creció a partir del proyecto de hardware libre para fabricación aditiva RepRap y, una vez consiguió cierta fuerza de mercado, dio un giro (quizá no muy grande) y abandonó el hardware libre. Stratasys tiene su peso en la industria, mientras que MakerBot se hizo un hueco en el mercado doméstico. Lo anunciado hoy es esto: MakerBot pasa a ser una filiar de Stratasys. Stratsys, por cierto, ya se había fusionado anteriormente con otra empresa de la competencia, Objet, el año pasado. El año anterior, 2011, Stratasys adquirió Solidscape. La cosa funciona así.
Los consumidores domésticos pueden recibir la noticia de hoy con dos enfoques diferentes:
- por una parte, es de esperar una mejora en la calidad de los productos de MakerBot, quizá hasta volverlos auténticamente útiles;
- por otra parte, la oferta se concentra en menos manos, lo que reduce los incentivos por presentar buenos productos a buenos precios.
Una fabricadora aditiva con control numérico no es lo que se dice un bien de primera necesidad, así que la pérdida de competencia no es tan grave como la que se produciría en el mercado de los alimentos, por ejemplo, pero no deja de ser molesta. Esto no es el fin del mercado para «manitas» que MakerBot abandonó hace tiempo, pero la cosa comercial está quedándose en manos muy grandes y eso nunca es bueno para los jugadores pequeños.
Categorías: Actualidad
Permalink: https://sgcg.es/articulos/2013/06/20/stratasys-compra-makerbot/
Vocabulario aeroespacial (6): «CAVOK»
2013-06-19
Hoy tenemos otro artículo de nuestra serie que introduce vocabulario aeroespacial. La sigla de hoy es «CAVOK», una forma muy corta de decir algo así como «buen tiempo». Viene de la expresión inglesa Cover And Visibility OK. Se usa en informes meteorológicos relacionados con un aeródromo y significa que se cumplen estos criterios:
- la cubierta de nubes se encuentra por encima de los 1500 m sobre el aeródromo o por encima de la mayor altitud mínima del sector, lo que sea más elevado;
- la visibilidad supera los 10 km.
Encontrar «CAVOK» en un informe meteorológico es a menudo una buena noticia, lo que explica la existencia de varias compañías relacionadas con la aeronáutica que contienen «CAVOK» en el nombre.
Categorías: Aeroespacio, Lingüística
Permalink: https://sgcg.es/articulos/2013/06/19/vocabulario-aeroespacial-6-cavok/
Un gracioso bulo sobre Marte
2013-06-17
Hoy recibí una presentación con un bulo muy gracioso sobre el planeta Marte. Decía que Marte y la Tierra iban a encontrarse este verano en una oposición extraordinaria, tan extraordinaria que iban a cumplirse los siguientes hechos notabilísimos:
- la distancia entre la Tierra y Marte iba a ser de 34649589 millones de kilómetros;
- Marte iba a ocupar una longitud de arco de 25,11 segundos;
- Marte iba a ser aparentemente más grande que la Luna.
Esto es una tontería muy divertida. Es una variación de un bulo que se repite en verano desde hace unos años. Analicemos esta versión punto por punto.
La Tierra y Marte van a estar a 34649589 millones de kilómetros
Esta distancia, unos 35 Pm, no es mucho menor que la que nos separa de Próxima Centauri. Probablemente, el «millones» es redundante; ignorémoslo.
La Tierra y Marte van a estar a 34649589 kilómetros
Esta distancia es mucho más razonable, pero quizá es algo próxima. Asumamos que las unidades son incorrectas. Una distancia de 34649589 millas o unos 55,76 Gm viene a ser la distancia entre la Tierra y Marte cuando están en oposición. Esto ya tiene buen aspecto.
Marte va a ocupar una longitud de arco de 25,11 segundos
Los ángulos son muy pequeños, así que podemos hacer una aproximación lineal y sustituir tangentes y arcotangentes por sus propios argumentos. Un cuerpo a una distancia d que ocupa una longitud de arco s en nuestro campo visual tiene un radio r que se estima mediante esta expresión:
r ≈ d s ⁄ 2.
En unidades civilizadas, la longitud de arco es s = 121,7 μrad. La distancia es d = 55,76 Gm, así que el radio es r ≈ 3,39 Mm. Esto es con muy buena aproximación el radio ecuatorial de Marte. Las cuentas empiezan a salir y no tienen nada de extraordinario.
Marte va a tener un tamaño aparente superior al de la Luna
Aquí llegamos a lo gracioso. La Luna tiene una órbita un poquito excéntrica; en el entorno del apogeo, la distancia d entre puntos de la superficie terrestre y el centro de la Luna es próxima a los 380 Mm. Esta distancia es fácil de estimar con un modelo muy simplificado. El radio r de la Luna es próximo a 1,74 Mm, así que el diámetro angular s, con la aproximación r ≈ d s ⁄ 2 de antes, queda en s ≈ 9,16 mrad. Vimos antes que el diámetro angular de Marte en la oposición es de unos 122 μrad, así que Marte tendría que tener 75 veces su radio para que tuviera el mismo tamaño aparente que la Luna: unos 255 Gm, lo que es algo más de tres veces y media el radio ecuatorial de Júpiter. No está nada mal.
Si la distancia hubiera sido de 34649589 millones de kilómetros, el radio de Marte habría tenido que ser de casi 160 Tm. Esto es unas ocho veces y media la distancia que separa la Tierra de la sonda Voyager 1.
Categorías: Miscelánea
Permalink: https://sgcg.es/articulos/2013/06/17/un-gracioso-bulo-sobre-marte/
La dificultad de mover una báscula
2013-06-15
Hay varias maneras de medir la masa de un objeto. Las más sencillas y conocidas funcionan gracias a que el peso de un cuerpo es proporcional a su masa: lo que hacen es pesar, pero del peso se deduce la masa. Hay de diferentes tipos, pero las que nos interesan hoy son las básculas que miden la fuerza del peso mediante muelles (las mecánicas) o células de carga (las electrónicas).
Relación entre el peso y la masa
Al pesar, medimos el peso, P, una fuerza que está relacionada con la masa M y la aceleración gravitatoria g de la siguiente manera:
P = M g.
Si se conoce la aceleración gravitatoria, el cálculo de la masa es inmediato. En la superficie terrestre, la aceleración gravitatoria es esencialmente igual a 9,8 m s−2. Si la báscula está horizontal, el peso queda bien medido.
Dificultades en las medidas precisas

Báscula de cocina. Funciona mediante un muelle dinamométrico.
La graduación de la escala es tal que tiene poca importancia la
variación del campo gravitatorio a lo largo y ancho de la superficie
terrestre. Si quisiéramos cambiar la calibración, tendríamos que
pintar una escala nueva.
Digamos que nos desplazamos a la otra punta del mundo y llevamos con nosotros nuestra báscula de cocina. Esta báscula no es muy precisa y las recetas de cocina son en general muy tolerantes a pequeñas variaciones en las proporciones de los ingredientes. En una situación así, no tenemos especial interés por hacer medidas con una precisión más fina que una centésima (pasar de 100 g a 101 g de harina probablemente no arruinará nuestro pastel), así que podemos usar la báscula de cocina sin preocuparnos. Si necesitamos hacer medidas más precisas que un punto porcentual, entonces estamos obligados a recalibrar nuestra báscula o a corregir lo que leemos de ella.

Báscula electrónica. Es posible calibrarla con masas de
referencia.
La Tierra no es una esfera perfecta y no está completamente inmóvil y aislada del resto del universo. Asumir esto es válido si solamente vamos a preparar un bizcocho, pero no si tenemos que medir la masa de un reactivo con una precisión de una milésima parte. Un mismo cuerpo no pesa lo mismo si está en Río de Janeiro que si está en Estocolmo. Las diferencias son próximas a cinco milésimas (la aceleración difiere en unos 5 cm s−2) entre las zonas de la superficie terrestre en las que el peso es mayor y en las que el peso es menor; son pequeñas para algunos fines, pero grandes para otros.
El origen de los diferentes pesos
Si usamos un modelo de gravitación de Newton, podemos achacar el grueso de las diferencias a la forma no completamente esférica de la Tierra y al efecto centrífugo debido a la rotación: la fuerza aparente proporcional a la masa de un cuerpo es la de gravedad más una de inercia que emerge al pasar de un sistema de referencia inercial a uno acelerado. El efecto centrífugo es máximo cerca del ecuador (donde la distancia al eje de rotación es máxima) y mínimo cerca de los polos (donde la distancia al eje de rotación es mínima). Su magnitud máxima Δgcentrífuga es fácil de estimar como el producto del cuadrado de la velocidad angular de rotación de la Tierra y su radio ecuatorial (ambos datos supuestos fijos, pues sus pequeñas variaciones suponen correcciones minúsculas que aplicar a un término correctivo que ya es pequeño):
Δgcentrífuga ≈ (2π ⁄ 86400 s)2 6378 km ≈ 34 mm s−2.
Esta magnitud es responsable de unas 3,5 milésimas de variación. La forma de la Tierra, es decir, su distribución de masa en el espacio y la localización de su superficie, aporta desviaciones por gravedad que son del mismo orden de magnitud que las centrífugas.
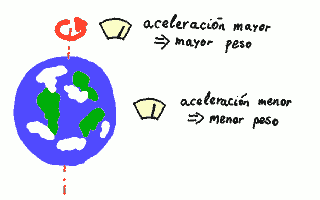
Diferentes pesos en diferentes puntos de la superficie terrestre.
La solución
Si necesitamos realizar medidas precisas, nos vemos obligados a corregir las lecturas de las básculas o a calibrarlas para la aceleración gravitatoria local. De forma alternativa, es posible usar aparatos de medida que anulan el efecto de las variaciones geográficas del campo de aceleraciones. Las balanzas y las básculas de contrapeso, si están realizadas de forma exquisita, son una buena opción.
Categorías: Física
Permalink: https://sgcg.es/articulos/2013/06/15/la-dificultad-de-mover-una-bascula/
Qué es eso del análisis dimensional (2): ejemplo de aplicación
2013-06-13
Presentamos anteriormente el concepto del análisis dimensional, un conjunto de herramientas de gran utilidad que se basa en el mero análisis de las dimensiones (es decir, de los tipos de magnitudes o, algo incorrectamente, de sus unidades de medida) de las variables físicas. Hoy vamos a ver una pequeña aplicación práctica.
El problema
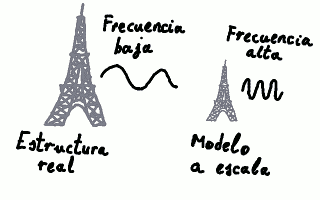
Necesitamos conocer una frecuencia de resonancia f de cierta estructura. En vez de hacer un ensayo de la estructura real, trabajamos con un modelo a escala y, quizá, realizado en otro material. Digamos que la estructura original es de acero y vamos a trabajar con un modelo a escala realizado en aluminio. La frecuencia de resonancia que buscamos depende de:
- la geometría, que es esencialmente la misma en el modelo a escala y en la estructura real;
- el tamaño de la estructura, que es Lreal en la estructura a tamaño real y Lescala en el modelo a escala;
- la densidad del material, que es ρreal en la estructura real y ρescala en el modelo a escala;
- las propiedades elásticas del material, que son el módulo elástico (Ereal en la estructura real y Eescala en el modelo a escala) y el coeficiente de Poisson (νreal en la estructura real y νescala en el modelo a escala), un número adimensional que es aproximadamente el mismo en el acero de la estructura a tamaño real y en el aluminio del modelo a escala.
Reducción de la complejidad del problema
Con la geometría fija, la frecuencia de resonancia todavía depende de cuatro parámetros. Ahora bien, ya vimos que el análisis dimensional nos da herrmientas para reducir el tamaño del problema. En efecto, vimos que podemos simplificar si tomamos algunas magnitudes como unidades de medida, con lo que efectivamente formamos grupos adimensionales tras escalar. En nuestro problema, tenemos tres dimensiones físicas: el tiempo [T], la longitud [L] y la masa [M]. Las distintas magnitudes tienen dimensiones que se obtienen a partir de ellas:
- la frecuencia de resonancia f tiene dimensiones del inverso de un tiempo, [T]−1;
- el tamaño L tiene dimensiones de longitud, [L];
- la densidad ρ tiene dimensiones de masa por unidad de volumen, [M] [L]−3;
- el módulo elástico E tiene dimensiones de presión, es decir, de masa dividida por longitud y por el cuadrado del tiempo, [M] [L]−1 [T]−2;
- el coeficiente de Poisson ν es adimensional, es decir, tiene la dimensión de la unidad, 1.
Usar algunas variables del problema como nuevas unidades de medida es equivalente a formar grupos adimensionales. El objetivo es, por lo tanto, multiplicar potencias de las variables hasta que todo tenga las dimensiones de la unidad. Sin mucho esfuerzo, vemos que podemos formar un grupo combinando la frecuencia, el tamaño, la densidad y el módulo elástico. El grupo es el siguiente:
f2 L2 ρ E−1.
Tenemos tres dimensiones físicas y hemos usado tres variables independientes (el tamaño L, la densidad ρ y el módulo elástico E) para definir las nuevas unidades de medida; por lo tanto, ya no nos quedan variables que eliminar. El grupo adimensional que nos ha salido, la frecuencia adimensional, depende de la única variable (ya adimensional) que queda: el coeficiente de Poisson ν.
Cómo escalar los resultados del experimento
La estructura real y el modelo a escala tienen casi
el mismo coeficiente de Poisson:
νreal
≈ νescala;
como este parámetro era el único que quedaba, podemos presumir
que la frecuencia adimensional es aproximadamente la misma si realmente
varía poco con el coeficiente de Poisson, lo que se cumple a menudo.
Queda la siguiente relación:
(freal)2 (Lreal)2 ρreal (Ereal)−1 ≈ (fescala)2 (Lescala)2 ρescala (Eescala)−1.
Con este minúsculo esfuerzo, hemos deducido cómo escala la frecuencia
de resonancia:
freal ≈ fescala (Lescala ⁄ Lreal) (ρescala ⁄ ρreal)1⁄2 (Ereal ⁄ Eescala)1⁄2.
El modelo a escala está hecho en aluminio y la estructura real está hecha de acero. Las proporciones de las densidades y las rigideces de estos materiales son tales que los términos correspondientes en la ecuación anterior dan un resultado que es casi 1, con lo que la frecuencia de resonancia de la estructura real de acero es muy aproximadamente la del modelo de aluminio multiplicada por el factor de escala.
Categorías: Física
Permalink: https://sgcg.es/articulos/2013/06/13/que-es-eso-del-analisis-dimensional-2-ejemplo-de-aplicacion/
Qué es eso del análisis dimensional
2013-06-10
El análisis dimensional es una herramienta muy útil en la física y otros campos científicos. Consiste, como indica su nombre, en analizar las dimensiones de las magnitudes físicas con fines diversos como verificar la corrección de un cálculo o reducir el número de variables de un modelo.
¿Cómo que las dimensiones de las magnitudes físicas?
La dimensión de una magnitud física es la naturaleza de dicha magnitud: si se trata de una longitud, de un tiempo, de una masa…
Al describir un sistema, podemos identificar algunas dimensiones como fundamentales y otras como derivadas. Por ejemplo, podemos tomar la longitud y el tiempo como fundamentales y considerar la velocidad como derivada al ser una longitud dividida por un tiempo; pero también podemos tomar la velocidad y el tiempo como fundamentales, lo que deja la longitud con dimensiones de velocidad multiplicada por tiempo.
El análisis dimensional como herramienta de verificación
Una propiedad muy útil que suelen tener los modelos físicos es que suelen estar expresados matemáticamente de forma tal que si hay dos términos sumados, ambos tienen las mismas dimensiones (el viejo cuento de sumar peras con peras y manzanas con manzanas); y en las ecuaciones, lo que aparece a un lado de una igualdad, tiene las mismas dimensiones que al otro lado de la igualdad (las superficies no son lo mismo que las longitudes, por ejemplo, así que no se igualan). Aquí el análisis dimensional es útil para descartar modelos infactibles e identificar ciertos errores de cálculo en los que las dimensiones quedan inconsistentes.
El análisis dimensional como herramienta simplificadora
Las magnitudes físicas están expresadas en función de unas unidades de medida que sirven de elementos de diferencia para las distintas dimensiones; por ejemplo, podemos expresar lo que tardamos en beber un vaso de agua como cierta cantidad de segundos, donde el segundo es la unidad de medida de tiempo. Ahora bien, contamos con que los sistemas físicos son independientes del conjunto de unidades de medida que usamos: a una pelota que rebota en el suelo le importa muy poco si usamos el Sistema Internacional o nos da por expresar las distancias en codos. Esto es algo notabilísimo, ya que permite reducir la complejidad de los modelos físicos. En efecto, como la física es independiente del sistema de unidades, podemos elegir como unidades algunas de las magnitudes del propio modelo físico con el que estamos trabajando. Por ejemplo, digamos que estamos diseñando una bicicleta y queremos determinar la rapidez de avance en función del régimen de pedaleo; tenemos las siguientes variables:
- la frecuencia de pedaleo, f, que es el inverso de un tiempo;
- el radio del plato, rplato, que es una longitud;
- el radio del piñón, rpiñón, que es una longitud;
- el radio de la rueda, rrueda, que es una longitud;
- la rapidez de avance, v, que es una longitud dividida por un tiempo.
Simbólicamente, estableceríamos la siguiente relación funcional en la que el símbolo F1(…) indica una cierta función:
V = F1(f, rplato, rpiñón, rrueda).
Parece que tenemos muchas variables, pero en realidad podemos reducir el tamaño del problema. En efecto, la física no depende del sistema de unidades de medida, así que nada nos impide usar las unidades que nos resulten más convenientes. Podemos tomar como unidad de tiempo el inverso de la frecuencia de pedaleo y como unidad de longitud el radio del plato; de esta manera, eliminamos de un plumazo dos de las cuatro variables independientes. De igual modo que si queremos pasar de usar segundos a usar minutos, lo que hacemos es dividir los tiempos por los segundos que hacen un minuto, aquí dividiremos los tiempos por nuestra nueva unidad de tiempo y las longitudes por nuestra nueva unidad de longitud. Como la rapidez es una longitud dividida por un tiempo, la multiplicamos por nuestra nueva unidad de tiempo y la dividimos por nuestra nueva unidad de longitud. Nos sale lo siguiente:
V ⁄ (f rplato) = F2(f ⁄ f, rplato ⁄ rplato, rpiñón ⁄ rplato, rrueda ⁄ rplato) = F2(1, 1, rpiñón ⁄ rplato, rrueda ⁄ rplato) = F3(rpiñón ⁄ rplato, rrueda ⁄ rplato).
Nuestro problema de diseño es realmente mucho más pequeño con estas nuevas variables. Estas variables, de las que realmente hemos eliminado las dimensiones al dividir por las unidades, son variables adimensionales.
El análisis dimensional como herramienta de reducción de resultados experimentales
Volvamos al caso anterior. Podemos hacer experimentos en los que tendremos valores diferentes de la rapidez, la frecuencia del pedaleo, el radio del plato, el radio del piñón y el radio de la rueda; ahora bien, si construimos variables adimensionales como hicimos arriba, podemos no solamente reducir el número de experimentos que necesitamos, sino que además podemos deducir rápidamente obtendríamos con otras combinaciones de los cuatro parámetros originales que dieran los mismos parámetros adimensionales; lo único que necesitamos es deshacer el cambio.
El análisis dimensional como herramienta predictiva y mnemotécnica
A veces, gracias al análisis dimensional, podemos saber qué forma va a tener la solución de un problema sin llegar a resolverlo. Digamos que tenemos un amplificador de audio al que añadimos un filtro creado con una resistencia y una capacidad. La frecuencia de corte f de nuestro filtro depende de alguna manera de estos dos parámetros. La resistencia es una tensión dividida por una intensidad de corriente, es decir, el producto de una tensión y un tiempo dividido por una carga. La capacidad es una carga dividida por una tensión. Con estos dos datos, sabemos que el producto de la resistencia y la capacidad es un tiempo. Como una frecuencia es el inverso de un tiempo, la frecuencia de corte tiene que ser inversamente proporcional al producto de la resistencia y la capacidad. Si conocemos la frecuencia de corte con una combinación de parámetros, ya sabemos cómo escalaría con una combinación de parámetros diferente.
Categorías: Física
Permalink: https://sgcg.es/articulos/2013/06/10/que-es-eso-del-analisis-dimensional/
Sencillo altavoz amplificado para emergencias
2013-06-06

Necesitaba urgentemente un pequeño altavoz con amplificador incorporado para unos ensayos con música. Este altavoz tenía que:
- ser pequeño, más pequeño que un puño, para poder llevarlo sin problemas en una mochila ya repleta de trastos;
- funcionar a pilas;
- ser capaz de producir un sonido bien distinguible a varios metros de distancia en un entorno ruidoso con tráfico rodado a alguna decena de metros de distancia;
- tener un diseño muy sencillo que permitiera una fabricación casera rápida.
La solución consistió en usar un cicruito integrado amplificador LM386 para mover un pequeño altavoz de 8 Ω y 57 mm de diámetro. La alimentación la da una pila de 9 V (6LR61) ayudada por un condensador de 100 μF que se come los transitorios y evita problemas cuando el volumen es alto. La ganancia máxima elegida es de 46 dB: la más grande que puede dar el circuito integrado amplificador y de sobra para hacer sonar bien altas señales muy, muy tenues. El volumen se ajusta a la entrada mediante un potenciómetro de 10 kΩ que, junto con los 50 kΩ de entrada que tiene el circuito integrado amplificador, da una impedancia de entrada de 8,3 kΩ, sin duda mucho más alta que la de los típicos auriculares para reproductor de música portátil. En principio, no es de esperar que la señal de una salida de auriculares tenga componente de continua, así que no hay condensador a la entrada. El circuito es muy sencillo y viene a ser como el que figura en la hoja de datos del fabricante para máxima ganancia.
Esquema del circuito

Aquí está el esquema en dos formatos de imagen:
El original está disponible en el formato editable de gEDA/gschem:
amplified-speaker.sch
Listado de componentes
Aquí están los componentes con los nombres que tienen en el esquema del circuito.
- R1
- Potenciómetro de panel de 10 kΩ. Sirve como control de volumen.
- R2
- Resistor de 10 Ω.
- C1
- Condensador electrolítico de 100 μF.
- C2
- Condensador electrolítico de 100 μF.
- C3
- Condensador electrolítico de 47 nF.
- C4
- Condensador electrolítico de 470 μF.
- U1
- Circuito integrado amplificador LM386.
- S1
- Interruptor de panel.
- B1
- Pila recargable de 9 V (con su portapilas).
- SPK1
- Altavoz miniatura de 57 mm y 8 Ω.
- T1
- Clavija jack de 3,5 mm con su cable correspondiente.
La clavija es estereofónica, pero el altavoz es monofónico. Los dos canales se juntan a la entrada. Podría haber comprado un par de clavija y cable monofónicos como alternativa.
Algunos componentes son comprados con el propósito de hacer el altavoz amplificado y otros estaban en inventario, lo que justifica su elección. El condensador C2 podría haber sido más pequeño, por ejemplo.
El interruptor S1 es uno de palanquita metálica.
Añadí al potenciómetro R1 un bonito mando.
Carcasa
La carcasa está hecha con cartón de una caja de galletas. Esto le da cierto carácter simpático y sorprendente.

Elaboración de la carcasa. La forma final es más delgada, de unos
3 cm de espesor.
Esta carcasa está realizada en dos piezas. La primera alberga los componentes y sirve de apoyo para el altavoz. La segunda es una tapa con una rejilla recortada que evita que el altavoz se mueva a la vez que lo protege. La tapa tiene cierto apriete que permite que se fije por fricción.

Las dos piezas de la carcasa.
El interruptor de encendido y el control de volumen atraviesan la carcasa y están fijos mediante tuercas. El cable de audio también atraviesa la carcasa y tiene un nudo que impide que los tirones se transmitan a las soldaduras.
La carcasa forma aproximadamente un prisma de algo menos de 8 cm de lado y alto y un poquito más de 3 cm de fondo.
Calidad del sonido
Como es de esperar, la calidad del audio es algo mejorable. El altavoz es pequeño y no hay compensación para los tonos extremos. Se escucha cierta estática. Es evidente que el aparato no satisfaría a un audiófilo con altas exigencias, pero está pensado para salir de un apuro con un diseño simple, pocos componentes discretos y un proceso de fabricación muy rápido.
Categorías: DIY, Electricidad
Permalink: https://sgcg.es/articulos/2013/06/06/sencillo-altavoz-amplificado-para-emergencias/
