El modelo epidemiológico SIR (10)
2020-04-18
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:
- cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia;
- el comportamiento de la proporción de infectados en esta fase inicial;
- cómo relacionar las variables sin necesidad de integrar en el tiempo;
- cómo calcular el máximo número de infectados simultáneos;
- cómo calcular el resultado final de la epidemia;
- cómo se comporta la epidemia en el entorno del máximo de infectados simultáneos;
- cómo varían los infectados cerca del final de la epidemia;
- cómo se relacionan la fase de crecimiento exponencial inicial de la epidemia y la fase de decrecimiento exponencial final de la epidemia.
Hoy veremos qué condición es necesaria para la inmunidad de grupo en este modelo.
Recordemos que el modelo sigue a lo largo del tiempo t la evolución de la proporción de susceptibles S(t), la proporción de infectados I(t) y la proporción de recuperados (inmunes y fallecidos) R(t) mediante el siguiente sistema de ecuaciones diferenciales ordinarias:
dS ⁄ dt = −(R0 ⁄ tI) S I;
dI ⁄ dt = (R0 ⁄ tI) S I − (1 ⁄ tI) I;
dR ⁄ dt = (1 ⁄ tI) I.
El parámetro R0 es el ritmo reproductivo básico: el número medio de contagios por infectado cuando toda la población es susceptible. El parámetro tI es el tiempo medio que permanece un paciente infectado.
La inmunidad de grupo se alcanza cuando la proporción de inmunes (R en este modelo) que la proporción de susceptibles es insuficiente para que, partiendo de una cantidad no nula de infectados, el número de infectados crezca. Es decir, ha de cumplirse lo siguiente:
dI ⁄ dt < 0.
De acuerdo con el modelo, la anterior condición implica esto:
(R0 ⁄ tI) S I − (1 ⁄ tI) I < 0.
Ahora bien, como el número de infectados de partida y la vida media de la infección son superiores a 0, la condición puede simplificarse un poco:
R0 S − 1 < 0.
Ahora bien, la población es constante en este modelo, así que se cumple que
S + I + R = 1,
con lo que tenemos la siguiente condición:
R0 (1−I−R) − 1 < 0.
Es inmediato dejar una condición explícita para los inmunes:
R > 1 − I − 1 ⁄ R0.
A partir del momento en el que se cumple esta condición, la infección empieza a disiparse. Una condición más exigente, que es válida independientemente de la proporción de infectados, es la siguiente:
R > 1 − 1 ⁄ R0.
Esta condición es la condición de inmunidad de grupo que implica que la epidemia no puede darse. El número acumulado de infecciones puede crecer a partir de un instante inicial, pero no de forma descontrolada, sino a un ritmo decreciente desde el primer momento.
La siguiente figura muestra, en función del ritmo reproductivo básico, el valor límite de la proporción de inmunes que hace falta de acuerdo con este modelo para alcanzar la inmunidad de grupo:
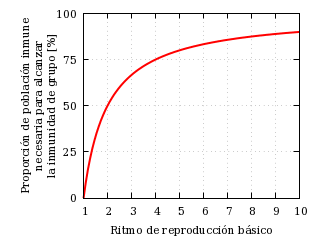
Inmunizados necesarios para alcanzar la inmunidad de grupo frente
al ritmo reproductivo básico.
Categorías: Matemáticas, Salud
Permalink: https://sgcg.es/articulos/2020/04/18/el-modelo-epidemiologico-sir-10/
