El modelo epidemiológico SIR (14)
2020-05-09
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:
- cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia;
- el comportamiento de la proporción de infectados en esta fase inicial;
- cómo relacionar las variables sin necesidad de integrar en el tiempo;
- cómo calcular el máximo número de infectados simultáneos;
- cómo calcular el resultado final de la epidemia;
- cómo se comporta la epidemia en el entorno del máximo de infectados simultáneos;
- cómo varían los infectados cerca del final de la epidemia;
- cómo se relacionan la fase de crecimiento exponencial inicial de la epidemia y la fase de decrecimiento exponencial final de la epidemia;
- qué condición es necesaria para la inmunidad de grupo;
- cómo queda modificado el modelo si en vez de trabajar con proporciones sobre la población total, trabajamos con números absolutos de individuos;
- cómo plantear el modelo cuando hay nacimientos y defunciones, pero la población total se mantiene estable;
- cómo extraer el ritmo reproductivo básico del modelo con natalidad y mortalidad en equilibrio.
Hoy identificaremos los puntos fijos o puntos de equilibrio del sistema referido a los susceptibles y los infectados.
Recordemos que el modelo sigue a lo largo del tiempo t la evolución de la población susceptible S(t), la población infectada I(t) y la población recuperada (inmune) R(t) mediante el siguiente sistema dinámico:
dS ⁄ dt = μ N − β S I ⁄ N − μ S;
dI ⁄ dt = β S I ⁄ N − γ I − μ I;
dR ⁄ dt = γ I − μ R.
Aparecen varios símbolos cuyo significado es el siguiente:
- El símbolo N denota la población total, S + I + R, que se mantiene constante. Como anteriormente, como la población es constante, es muy cómodo tomar N = 1 y trabajar con proporciones de la población total.
- El símbolo μ denota tanto la natalidad como la mortalidad, que son iguales.
- El símbolo β denota la tasa de infección. Vimos que está relacionado con el ritmo reproductivo básico R0 (los nuevos contagios que provoca el caso inicial) mediante la relación R0 = (γ+μ) β.
- El símbolo γ denota la tasa de recuperación de los infectados. En anteriores artículos era el inverso del tiempo infeccioso promedio, pero ahora las defunciones complican un poco la interpretación.
Para estudiar cualitativamente cómo se comporta el modelo en función de los parámetros, podemos tomar N como unidad de población (de manera N = 1 en las ecuaciones y trabajamos con proporciones sobre la población total como en los primeros artículos) y γ−1 como unidad de tiempo (de manera que γ = 1 en las ecuaciones). Este escalado de los parámetros es razonable en todas las situaciones físicamente posibles salvo en el caso degenerado de una enfermedad sin posible recuperación (γ = 0, que sería el modelo SI, sin estado R). Las ecuaciones quedan un poco más sencillas:
dS ⁄ dt = μ − (1+μ) R0 S I − μ S;
dI ⁄ dt = (1+μ) R0 S I − (1+μ) I.
Como S + I + R = 1, el modelo es realmente bidimensional y no tridimensional, así que hemos obviado la variable R por ser redundante.
Las ecuaciones tienen dos puntos fijos en los que ni S ni I varían:
S = 1, I = 0;
S = 1 ⁄ R0, I = [μ ⁄ (1+μ)] [(R0−1) ⁄ R0].
El primer punto fijo es el equilibrio libre de enfermedad: toda la población permanece infectada. El segundo punto fijo es el equilibrio endémico: los nuevos susceptibles que tras nacer se infectan equilibran las muertes y recuperaciones. En los próximos artículos exploraremos la naturaleza de estos puntos fijos; hoy es suficiente localizarlos.
El equilibrio libre de enfermedad no se mueve con los parámetros. El equilibrio endémico sí se mueve, pero es evidente que lo hace en la siguiente recta:
I = [μ ⁄ (1+μ)] (1−S).
El equilibrio endémico solamente tiene sentido físico cuando el ritmo reproductivo es igual o mayor que la unidad. Los susceptibles parten de ser toda la población a anularse cuando el ritmo reproductivo básico tiende a infinito. Los infectados parten de ser nulos a ser [μ ⁄ (1+μ)] cuando el ritmo reproductivo básico tiende a infinito.
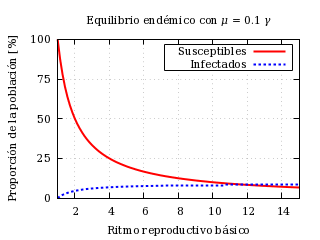
Equilibrio endémico frente al ritmo reproductivo básico para
cierto valor de la tasa de natalidad y mortalidad.
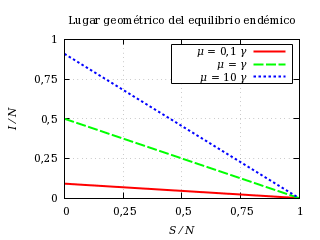
Lugar geométrico del equilibrio endémico para distintos valores de
la tasa de natalidad y mortalidad.
Categorías: Matemáticas, Salud
Permalink: https://sgcg.es/articulos/2020/05/09/el-modelo-epidemiologico-sir-14/
