El modelo epidemiológico SIR (16)
2020-05-20
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:
- cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia;
- el comportamiento de la proporción de infectados en esta fase inicial;
- cómo relacionar las variables sin necesidad de integrar en el tiempo;
- cómo calcular el máximo número de infectados simultáneos;
- cómo calcular el resultado final de la epidemia;
- cómo se comporta la epidemia en el entorno del máximo de infectados simultáneos;
- cómo varían los infectados cerca del final de la epidemia;
- cómo se relacionan la fase de crecimiento exponencial inicial de la epidemia y la fase de decrecimiento exponencial final de la epidemia;
- qué condición es necesaria para la inmunidad de grupo;
- cómo queda modificado el modelo si en vez de trabajar con proporciones sobre la población total, trabajamos con números absolutos de individuos;
- cómo plantear el modelo cuando hay nacimientos y defunciones, pero la población total se mantiene estable;
- cómo extraer el ritmo reproductivo básico del modelo con natalidad y mortalidad en equilibrio;
- los puntos fijos o puntos de equilibrio del sistema referido a los susceptibles y los infectados;
- la naturaleza del punto de equilibrio libre de enfermedad.
Hoy investigaremos la naturaleza del equilibrio endémico.
Recordemos que estamos estudiando los puntos fijos del siguiente sistema:
dS ⁄ dt = μ − (1+μ) R0 S I − μ S;
dI ⁄ dt = (1+μ) R0 S I − (1+μ) I.
Aparecen varios símbolos cuyo significado es el siguiente:
- La variable dependiente S es la proporción susceptible de la población total.
- La variable dependiente I es la proporción de la población infectada.
- La variable independiente t es el tiempo hecho adimensional de forma que la población infectada pasa a ser población recuperada a un ritmo por unidad de tiempo adimensional igual a la propia población infectada. El primer artículo sobre los puntos fijos explica esto.
- El símbolo μ denota tanto la natalidad como la mortalidad, que son iguales.
- El símbolo R0 es el ritmo reproductivo básico (los nuevos contagios que provoca el caso inicial).
El equilibrio endémico es el siguiente punto:
S = 1 ⁄ R0, I = [μ ⁄ (1+μ)] [(R0−1) ⁄ R0].
Como tanto R0 como μ solamente tienen sentido físico cuando tienen valores no negativos, para que haya equilibrio endémico con una cantidad de infectados positiva es necesario que R0 ≥ 1. que μ > 0.
Las derivadas temporales se anulan en el punto de equilibrio endémico. La matriz jacobiana tiene los autovalores:
- −(R0 μ ⁄ 2)+√[(R0 μ ⁄ 2)2−(μ+μ2) (R0−1)];
- −(R0 μ ⁄ 2)−√[(R0 μ ⁄ 2)2−(μ+μ2) (R0−1)].
Como partimos de R0 > 1 y μ > 0, la parte real de los autovalores siempre es negativa y, por lo tanto, el equilibrio endémico es estable. La naturaleza precisa del punto de equilibrio endémico depende de si los autovalores son reales o tienen parte imaginaria no nula, que a su vez depende de la relación de R0 y μ:
- Si 1 < R0 < (2 ⁄ μ) [1+μ−√(1+μ)], el equilibrio endémico es un nodo estable, con dos direcciones principales diferentes. En función del tiempo, los susceptibles y los infectados acaban convergiendo exponencialmente al punto de equilibrio endémico.
- Si R0 = (2 ⁄ μ) [1+μ−√(1+μ)], el equilibrio endémico es un nodo degenerado estable, con solamente una dirección principal. En función del tiempo, los susceptibles y los infectados acaban convergiendo exponencialmente al punto de equilibrio endémico según una dirección que converge a ∆I = {[1 ⁄ √(1+μ)]−1} ∆S, donde ∆S y ∆S son la diferencia que tienen los susceptibles y los infectados, respectivamente, con sus valores endémicos.
- Si (2 ⁄ μ) [1+μ−√(1+μ)] < R0 < (2 ⁄ μ) [1+μ+√(1+μ)], el equilibrio es una espiral atractora. Las trayectorias próximas al equilibrio endémico se acercan a este punto según una espiral. En función del tiempo, tanto los susceptibles como los infectados oscilan con amplitud exponencialmente decreciente para converger a sus respectivos valores en el equilibrio endémico.
- Si R0 = (2 ⁄ μ) [1+μ+√(1+μ)], el equilibrio endémico es un nodo degenerado estable, con solamente una dirección principal. En función del tiempo, los susceptibles y los infectados acaban convergiendo exponencialmente al punto de equilibrio endémico según una dirección que converge a ∆I = {−[1 ⁄ √(1+μ)]−1} ∆S, donde ∆S y ∆S son la diferencia que tienen los susceptibles y los infectados, respectivamente, con sus valores endémicos.
- Si R0 > (2 ⁄ μ) [1+μ+√(1+μ)], el equilibrio endémico es nodo estable, con dos direcciones principales distintas. En función del tiempo, los susceptibles y los infectados acaban convergiendo exponencialmente al punto de equilibrio endémico.
La siguiente figura muestra un ejemplo del lugar geométrico de los autovalores del jacobiano en el equilibrio endémico cuando se varía R0 con un valor de μ fijo:
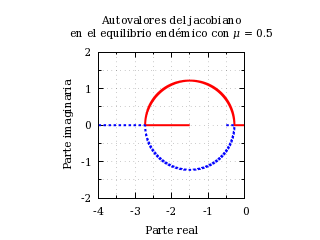
Lugar geométrico de los autovalores del jacobiano en el equilibrio
endémico.
Echemos un vistazo a este lugar geométrico de los autovalores:
- En el límite R0 → 1, uno de los autovalores (el representado por la línea continua) se hace 0 y el otro (el representado por la línea de trazos) se hace −μ. Es el caso límite en el que no hay epidemia (el equilibrio endémico es el equilibrio libre de enfermedad).
- Conforme crece el valor de R0 por debajo de (2 ⁄ μ) [1+μ−√(1+μ)], ambos autovalores se acercan por el eje real a 1+μ−√(1+μ). El equilibrio endémico es un nodo atractor.
- Con R0 = (2 ⁄ μ) [1+μ−√(1+μ)], ambos autovalores coinciden en −[1+μ−√(1+μ)]. El equilibrio endémico en este punto es un nodo atractor degenerado.
- Con (2 ⁄ μ) [1+μ−√(1+μ)] < R0 < (2 ⁄ μ) [1+μ+√(1+μ)], los autovalores se mueven en el plano complejo por una circunferencia con centro en −(1+μ) y radio √(1+μ). El autovalor que partía de 0 (el de la línea continua en la figura) tiene parte imaginaria positiva y el autovalor que partía de −μ (el de la línea de trazos en la figura) tiene parte imaginaria negativa. La parte imaginaria tiene una magnitud máxima (igual al radio) cuando R0 = 2 [(1+μ) ⁄ μ]. El equilibrio endémico es una espiral que converge más rápido conforme crece R0 y que oscila a máxima frecuencia cuando R0 = 2 [(1+μ) ⁄ μ.
- Con R0 = (2 ⁄ μ) [1+μ+√(1+μ)], ambos autovalores coinciden en −[1+μ−√(1+μ)]. El equilibrio endémico en este punto es un nodo atractor degenerado.
- Con R0 > (2 ⁄ μ) [1+μ+√(1+μ)], ambos autovalores vuelven a separarse por el eje real. El equilibrio endémico es un nodo atractor.
- En el límite R0 → ∞, el autovalor que partía de 0 (el de la línea continua en la figura) tiende a −(1+μ) y el que partía de −μ (el de la línea de trazos en la figura) tiende a −∞. El equilibrio endémico es un nodo atractor con una dirección infinitamente rápida.
Categorías: Matemáticas, Salud
Permalink: https://sgcg.es/articulos/2020/05/20/el-modelo-epidemiologico-sir-16/
