El modelo epidemiológico SIR (17)
2020-05-24
El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:
- cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia;
- el comportamiento de la proporción de infectados en esta fase inicial;
- cómo relacionar las variables sin necesidad de integrar en el tiempo;
- cómo calcular el máximo número de infectados simultáneos;
- cómo calcular el resultado final de la epidemia;
- cómo se comporta la epidemia en el entorno del máximo de infectados simultáneos;
- cómo varían los infectados cerca del final de la epidemia;
- cómo se relacionan la fase de crecimiento exponencial inicial de la epidemia y la fase de decrecimiento exponencial final de la epidemia;
- qué condición es necesaria para la inmunidad de grupo;
- cómo queda modificado el modelo si en vez de trabajar con proporciones sobre la población total, trabajamos con números absolutos de individuos;
- cómo plantear el modelo cuando hay nacimientos y defunciones, pero la población total se mantiene estable;
- cómo extraer el ritmo reproductivo básico del modelo con natalidad y mortalidad en equilibrio;
- los puntos fijos o puntos de equilibrio del sistema referido a los susceptibles y los infectados;
- la naturaleza del punto de equilibrio libre de enfermedad;
- la naturaleza del equilibrio endémico.
Hoy vamos a ver que las soluciones del modelo siempre tienen sentido físico (es decir, no se producen cantidades imposibles de susceptibles, infectados o la combinación de ambos). Esto no significa necesariamente que el modelo tenga siempre buena capacidad predictiva, ya que asume cosas que no siempre son acertadas.
Recordemos que estamos estudiando los puntos fijos del siguiente sistema:
dS ⁄ dt = μ − (1+μ) R0 S I − μ S;
dI ⁄ dt = (1+μ) R0 S I − (1+μ) I.
Aparecen varios símbolos cuyo significado es el siguiente:
- La variable dependiente S es la proporción susceptible de la población total.
- La variable dependiente I es la proporción de la población infectada.
- La variable independiente t es el tiempo hecho adimensional de forma que la población infectada pasa a ser población recuperada a un ritmo por unidad de tiempo adimensional igual a la propia población infectada. El primer artículo sobre los puntos fijos explica esto.
- El símbolo μ denota tanto la natalidad como la mortalidad, que son iguales. Este número es nulo en el caso en el que no hay nacimientos ni muertes (o cuando se producen a un ritmo tan lento que es legítimo despreciar su efecto) y es positivo en el caso más general.
- El símbolo R0 es el ritmo reproductivo básico (los nuevos contagios que provoca el caso inicial). Este número es nulo en el caso trivial de una enfermedad que no se contagia y positivo en el caso general de las enfermedades contagiosas.
Las soluciones con significado físico siempre cumplen las siguientes condiciones:
- El número de susceptibles no puede ser negativo: S ≥ 0.
- El número de infectados no puede ser negativo: I ≥ 0.
- La suma de susceptibles e infectados nunca puede superar la población total: S + I ≤ 1. Esta condición en combinación con las dos anteriores implica que 0 ≤ S ≤ 1 y que 0 ≤ I ≤ 1.
En el plano S, I, esta región con sentido físico es un triángulo.
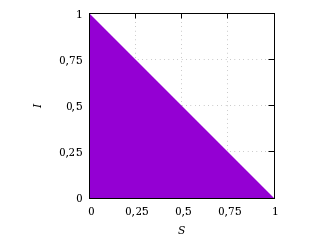
Región con sentido físico (área sombreada).
La pregunta que podemos hacernos es la siguiente: al partir de un punto dentro de la región con significado físico, ¿se mantiene la solución en ella conforme evoluciona? Veamos que en efecto, se mantiene allí.
Los susceptibles no pueden hacerse negativos
Para que sea posible pasar de S no negativo a S negativo, es necesario que se cumpla dS ⁄ dt < 0 en algún punto con S = 0. Ahora bien, se comprueba que dS ⁄ dt = μ ≥ 0 en el contorno S = 0, 0 ≤ I ≤ 1. Por lo tanto, las soluciones que parten de ese contorno o de su entorno dentro de la región con sentido físico bien van a mantenerse con S = 0, bien van a pasar a S ≥ 0. Se cumple que si se parte de cualquier punto en la región con sentido físico (incluido el contorno), la cantidad S de susceptibles nunca se hace negativa.
Los infectados no pueden hacerse negativos
Para que sea posible pasar de I no negativo a I negativo, es necesario que se cumpla en algún punto con dI ⁄ dt < 0 en S = 0. Ahora bien, se comprueba que dI ⁄ dt = 0 en el contorno I = 0, 0 ≤ S ≤ 1. Por lo tanto, cualquier solución que llegue a dicho contorno desde la región con sentido físico nunca va a a evolucionar a I < 0. Se cumple que si se parte de un punto cualquiera en la región con sentido físico (incluido el contorno), la cantidad I de infectados nunca se hace negativa.
La suma de susceptibles e infectados nunca puede superar a la población total
Para que sea posible pasar de S+I = 1 a S+I < 1, es necesario que se cumpla d(S+I) ⁄ dt > 1 en algún punto con S+I = 1. La suma S+I de susceptibles e infectados evoluciona en el tiempo en cumplimiento de d(S+I) ⁄ dt = dS ⁄ dt+dI ⁄ dt = (1−S−I) μ − I. Ahora bien, (1−S−I) μ − I = −I ≤ 0 cuando S+I = 1 y 0 ≤ I ≤ 1. Por lo tanto, cualquier solución que llegue a dicho contorno desde la región con sentido físico nunca va a a evolucionar a S+I > 1. Se cumple que si se parte de un punto cualquiera en la región con sentido físico (incluido el contorno), la suma S+I nunca supera la población total.
Conclusión: las soluciones están confinadas en la región con sentido físico
Todo lo anterior implica que si una solución pasa por un punto con sentido físico, se mantiene siempre dentro de la región con sentido físico.
Hemos ignorado la cantidad R de recuperados, pero ya se vio en anteriores artículos que d(S+I+R) ⁄ dt = 0. Por lo tanto, si se parte de una condición inicial tal que S+I+R = 1, sigue cumpliéndose S+I+R = 1 siempre. Por lo tanto, R = 1−S−I ≥ 0 y R ≤ 1 en la región con sentido físico. El número de recuperados nunca es negativo y nunca supera la población total.
Categorías: Matemáticas, Salud
Permalink: https://sgcg.es/articulos/2020/05/24/el-modelo-epidemiologico-sir-17/
