Mayo de 2020

lu	ma	mi	ju	vi	sá	do
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30	31

Cardo

2020-05-31

Tengo una lente de efectos especiales que encuentro divertida de usar de vez en cuando. La lente tiene mucha aberración esférica, que es algo que habitualmente es poco deseable, pero que a ciertos motivos les confiere un brillo misterioso y mágico. Aquí está una prueba realizada con un cardo árbol hace unos meses.

Fotografía de un cardo tomada con una lente de efectos especiales. Más grande.

Categorías: Fotografía

Permalink: http://sgcg.es/articulos/2020/05/31/cardo/

Boeing anuncia más de 12000 despidos

2020-05-29

Boeing, una de las mayores empresas de la industria aeronáutica del mundo, ha anunciado que despedirá a más de 12000 trabajadores en Estados Unidos.

Recientemente, los problemas del 737 Max llevaron a la detención temporal de la producción de la aeronave hace unos meses con un anuncio de la intención de que esto no se tradujera en eliminación de puestos de trabajo. En abril se reanudó tímidamente la producción, pero la actual crisis sanitaria global, de forma comprensible, se ha traducido en un parón difícil de aguantar en el sector del transporte aéreo. Lo que no pudo hacer el desastre del 737 Max ha terminado causándolo una epidemia devastadora.

Categorías: Actualidad, Aeroespacio

Permalink: http://sgcg.es/articulos/2020/05/29/boeing-anuncia-mas-de-12000-despidos/

El modelo epidemiológico SIR (18)

2020-05-26

El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:

Hoy vamos a ver que las soluciones siempre convergen a algún punto de equilibrio (bien el equilibrio endémico, bien el equilibrio libre de enfermedad). Para que el modelo contemplara otros comportamientos como oscilaciones periódicas o incluso caos, haría falta añadir complicaciones adicionales (parámetros variables en el tiempo, por ejemplo).

Recordemos que estamos estudiando los puntos fijos del siguiente sistema:

dS ⁄ dt = μ − (1+μ) R₀ S I − μ S;

dI ⁄ dt = (1+μ) R₀ S I − (1+μ) I.

Aparecen varios símbolos cuyo significado es el siguiente:

La variable dependiente S es la proporción susceptible de la población total.
La variable dependiente I es la proporción de la población infectada.
La variable independiente t es el tiempo hecho adimensional de forma que la población infectada pasa a ser población recuperada a un ritmo por unidad de tiempo adimensional igual a la propia población infectada. El primer artículo sobre los puntos fijos explica esto.
El símbolo μ denota tanto la natalidad como la mortalidad, que son iguales. Este número es nulo en el caso en el que no hay nacimientos ni muertes (o cuando se producen a un ritmo tan lento que es legítimo despreciar su efecto) y es positivo en el caso más general.
El símbolo R₀ es el ritmo reproductivo básico (los nuevos contagios que provoca el caso inicial). Este número es nulo en el caso trivial de una enfermedad que no se contagia y positivo en el caso general de las enfermedades contagiosas.

Posibles comportamientos a largo plazo

El sistema tiene dos dimensiones, las variables están confinadas en una región finita y las derivadas siguen funciones analíticas de las variables, así que podemos descartar comportamientos problemáticos (divergencias, caos…) y no queda más remedio que las soluciones bien acaben convergiendo a algún punto fijo, bien formen órbitas cerradas en el plano de fase (oscilen de forma periódica en el tiempo). Vamos a ver, además, que las órbitas cerradas no son posibles, lo que obliga a que las soluciones converjan a puntos fijos (el equilibrio libre de enfermedad y el equilibrio endémico).

Las órbitas cerradas no son posibles

Podemos descartar las órbitas cerradas si hacemos uso del teorema de Bendixson-Dulac con 1 ⁄ I como función de Dulac. Sea C una hipotética trayectoria cerrada dentro de la región 0 ≤ S, 0 < I, S+I ≤ 1 (luego veremos qué sucede si la curva pasa por I = 0) y sea D la región interior a este contorno. El teorema de Green dice lo siguiente:

∮_C[(1 ⁄ I) (dS ⁄ dt) dI − (1 ⁄ I) (dI ⁄ dt) dS] = ∬_D{(∂ ⁄ ∂S) [(1 ⁄ I) (dS ⁄ dt)] + (∂ ⁄ ∂I) [(1 ⁄ I) (dI ⁄ dt)]} dS dI = ∬_D[−(μ ⁄ I) − (1+μ) R₀] dS dI < 0.

Por otra parte, una trayectoria cerrada tendría que cumplir esto:

∮_C[(1 ⁄ I) (dS ⁄ dt) dI − (1 ⁄ I) (dI ⁄ dt) dS] = ∮_C(1 ⁄ I) [(dS ⁄ dt) (dI ⁄ dt) − (dI ⁄ dt) (dS ⁄ dt)] dt = 0.

Esto contradice el resultado del teorema de Green, así que no es posible. No existen trayectorias cerradas en el conjunto 0 ≤ S, 0 < I, S+I ≤ 1.

Queda ver, por supuesto, qué sucede con el contorno I = 0, 0 ≤ S ≤ 1. El sistema se reduce a dS ⁄ dt = μ − μ S, dI ⁄ dt, cuyas soluciones que parten desde cualquier punto del sistema estudiado bien convergen al equilibrio endémico S = 1, I = 0 cuando μ ≥ 0, bien directamente permanecen estacionarias cuando μ = 0; por lo tanto, este contorno no es parte de una órbita cerrada.

Lo visto en los anteriores párrafos hace descartar las órbitas cerradas en el espacio de fase, es decir, las soluciones periódicas en el tiempo.

Las soluciones acaban convergiendo a puntos fijos

Tras descartar otras posibilidades, vemos que no queda más remedio que las soluciones acaben convergiendo a puntos fijos.

Con μ = 0, ya vimos en su momento que las soluciones convergen a algún punto del eje I = 0. No hay un único punto fijo, sino que la situación es degenerada: todo I = 0 es fijo y además es atractor cuando S < 1 ⁄ R₀.
Con μ > 0 y 0 < R₀ ≤ 1, no hay equilibrio endémico y las soluciones han de converger forzosamente al equilibrio libre de enfermedad.
Con μ > 0 y R₀ > 1, el equilibrio endémico existe y es un bien un nodo atractor (las soluciones convergen sin oscilar), bien una espiral atractora (las soluciones convergen oscilando de forma amortiguada). El equilibrio libre de enfermedad, en cambio, es un punto silla, solamente atractor en una dirección (en concreto, atrae en todo el eje I = 0). Por lo tanto, las soluciones que parten de I = 0 acaban en el equilibrio libre de enfermedad y todas las demás acaban en el equilibrio endémico.

Categorías: Matemáticas, Salud

Permalink: http://sgcg.es/articulos/2020/05/26/el-modelo-epidemiologico-sir-18/

El modelo epidemiológico SIR (17)

2020-05-24

El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:

Hoy vamos a ver que las soluciones del modelo siempre tienen sentido físico (es decir, no se producen cantidades imposibles de susceptibles, infectados o la combinación de ambos). Esto no significa necesariamente que el modelo tenga siempre buena capacidad predictiva, ya que asume cosas que no siempre son acertadas.

Recordemos que estamos estudiando los puntos fijos del siguiente sistema:

dS ⁄ dt = μ − (1+μ) R₀ S I − μ S;

dI ⁄ dt = (1+μ) R₀ S I − (1+μ) I.

Aparecen varios símbolos cuyo significado es el siguiente:

La variable dependiente S es la proporción susceptible de la población total.
La variable dependiente I es la proporción de la población infectada.
La variable independiente t es el tiempo hecho adimensional de forma que la población infectada pasa a ser población recuperada a un ritmo por unidad de tiempo adimensional igual a la propia población infectada. El primer artículo sobre los puntos fijos explica esto.
El símbolo μ denota tanto la natalidad como la mortalidad, que son iguales. Este número es nulo en el caso en el que no hay nacimientos ni muertes (o cuando se producen a un ritmo tan lento que es legítimo despreciar su efecto) y es positivo en el caso más general.
El símbolo R₀ es el ritmo reproductivo básico (los nuevos contagios que provoca el caso inicial). Este número es nulo en el caso trivial de una enfermedad que no se contagia y positivo en el caso general de las enfermedades contagiosas.

Las soluciones con significado físico siempre cumplen las siguientes condiciones:

El número de susceptibles no puede ser negativo: S ≥ 0.
El número de infectados no puede ser negativo: I ≥ 0.
La suma de susceptibles e infectados nunca puede superar la población total: S + I ≤ 1. Esta condición en combinación con las dos anteriores implica que 0 ≤ S ≤ 1 y que 0 ≤ I ≤ 1.

En el plano S, I, esta región con sentido físico es un triángulo.

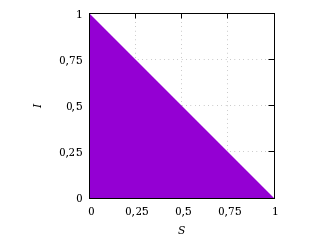
Región con sentido físico (área sombreada).

La pregunta que podemos hacernos es la siguiente: al partir de un punto dentro de la región con significado físico, ¿se mantiene la solución en ella conforme evoluciona? Veamos que en efecto, se mantiene allí.

Los susceptibles no pueden hacerse negativos

Para que sea posible pasar de S no negativo a S negativo, es necesario que se cumpla dS ⁄ dt < 0 en algún punto con S = 0. Ahora bien, se comprueba que dS ⁄ dt = μ ≥ 0 en el contorno S = 0, 0 ≤ I ≤ 1. Por lo tanto, las soluciones que parten de ese contorno o de su entorno dentro de la región con sentido físico bien van a mantenerse con S = 0, bien van a pasar a S ≥ 0. Se cumple que si se parte de cualquier punto en la región con sentido físico (incluido el contorno), la cantidad S de susceptibles nunca se hace negativa.

Los infectados no pueden hacerse negativos

Para que sea posible pasar de I no negativo a I negativo, es necesario que se cumpla en algún punto con dI ⁄ dt < 0 en S = 0. Ahora bien, se comprueba que dI ⁄ dt = 0 en el contorno I = 0, 0 ≤ S ≤ 1. Por lo tanto, cualquier solución que llegue a dicho contorno desde la región con sentido físico nunca va a a evolucionar a I < 0. Se cumple que si se parte de un punto cualquiera en la región con sentido físico (incluido el contorno), la cantidad I de infectados nunca se hace negativa.

La suma de susceptibles e infectados nunca puede superar a la población total

Para que sea posible pasar de S+I = 1 a S+I < 1, es necesario que se cumpla d(S+I) ⁄ dt > 1 en algún punto con S+I = 1. La suma S+I de susceptibles e infectados evoluciona en el tiempo en cumplimiento de d(S+I) ⁄ dt = dS ⁄ dt+dI ⁄ dt = (1−S−I) μ − I. Ahora bien, (1−S−I) μ − I = −I ≤ 0 cuando S+I = 1 y 0 ≤ I ≤ 1. Por lo tanto, cualquier solución que llegue a dicho contorno desde la región con sentido físico nunca va a a evolucionar a S+I > 1. Se cumple que si se parte de un punto cualquiera en la región con sentido físico (incluido el contorno), la suma S+I nunca supera la población total.

Conclusión: las soluciones están confinadas en la región con sentido físico

Todo lo anterior implica que si una solución pasa por un punto con sentido físico, se mantiene siempre dentro de la región con sentido físico.

Hemos ignorado la cantidad R de recuperados, pero ya se vio en anteriores artículos que d(S+I+R) ⁄ dt = 0. Por lo tanto, si se parte de una condición inicial tal que S+I+R = 1, sigue cumpliéndose S+I+R = 1 siempre. Por lo tanto, R = 1−S−I ≥ 0 y R ≤ 1 en la región con sentido físico. El número de recuperados nunca es negativo y nunca supera la población total.

Categorías: Matemáticas, Salud

Permalink: http://sgcg.es/articulos/2020/05/24/el-modelo-epidemiologico-sir-17/

Liquen

2020-05-23

Tengo una lente de efectos especiales que encuentro divertida de usar de vez en cuando. La lente tiene mucha aberración esférica, que es algo que habitualmente es poco deseable, pero que a ciertos motivos les confiere un brillo misterioso y mágico. Aquí está una prueba realizada con un liquen que crecía en la corteza de un árbol hace unos meses.

Fotografía de un liquen tomada con una lente de efectos especiales. Más grande.

Categorías: Fotografía

Permalink: http://sgcg.es/articulos/2020/05/23/liquen/

El modelo epidemiológico SIR (16)

2020-05-20

El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:

Hoy investigaremos la naturaleza del equilibrio endémico.

Recordemos que estamos estudiando los puntos fijos del siguiente sistema:

dS ⁄ dt = μ − (1+μ) R₀ S I − μ S;

dI ⁄ dt = (1+μ) R₀ S I − (1+μ) I.

Aparecen varios símbolos cuyo significado es el siguiente:

La variable dependiente S es la proporción susceptible de la población total.
La variable dependiente I es la proporción de la población infectada.
La variable independiente t es el tiempo hecho adimensional de forma que la población infectada pasa a ser población recuperada a un ritmo por unidad de tiempo adimensional igual a la propia población infectada. El primer artículo sobre los puntos fijos explica esto.
El símbolo μ denota tanto la natalidad como la mortalidad, que son iguales.
El símbolo R₀ es el ritmo reproductivo básico (los nuevos contagios que provoca el caso inicial).

El equilibrio endémico es el siguiente punto:

S = 1 ⁄ R₀, I = [μ ⁄ (1+μ)] [(R₀−1) ⁄ R₀].

Como tanto R₀ como μ solamente tienen sentido físico cuando tienen valores no negativos, para que haya equilibrio endémico con una cantidad de infectados positiva es necesario que R₀ ≥ 1. que μ > 0.

Las derivadas temporales se anulan en el punto de equilibrio endémico. La matriz jacobiana tiene los autovalores:

−(R₀ μ ⁄ 2)+√[(R₀ μ ⁄ 2)²−(μ+μ²) (R₀−1)];
−(R₀ μ ⁄ 2)−√[(R₀ μ ⁄ 2)²−(μ+μ²) (R₀−1)].

Como partimos de R₀ > 1 y μ > 0, la parte real de los autovalores siempre es negativa y, por lo tanto, el equilibrio endémico es estable. La naturaleza precisa del punto de equilibrio endémico depende de si los autovalores son reales o tienen parte imaginaria no nula, que a su vez depende de la relación de R₀ y μ:

Si 1 < R₀ < (2 ⁄ μ) [1+μ−√(1+μ)], el equilibrio endémico es un nodo estable, con dos direcciones principales diferentes. En función del tiempo, los susceptibles y los infectados acaban convergiendo exponencialmente al punto de equilibrio endémico.
Si R₀ = (2 ⁄ μ) [1+μ−√(1+μ)], el equilibrio endémico es un nodo degenerado estable, con solamente una dirección principal. En función del tiempo, los susceptibles y los infectados acaban convergiendo exponencialmente al punto de equilibrio endémico según una dirección que converge a ∆I = {[1 ⁄ √(1+μ)]−1} ∆S, donde ∆S y ∆S son la diferencia que tienen los susceptibles y los infectados, respectivamente, con sus valores endémicos.
Si (2 ⁄ μ) [1+μ−√(1+μ)] < R₀ < (2 ⁄ μ) [1+μ+√(1+μ)], el equilibrio es una espiral atractora. Las trayectorias próximas al equilibrio endémico se acercan a este punto según una espiral. En función del tiempo, tanto los susceptibles como los infectados oscilan con amplitud exponencialmente decreciente para converger a sus respectivos valores en el equilibrio endémico.
Si R₀ = (2 ⁄ μ) [1+μ+√(1+μ)], el equilibrio endémico es un nodo degenerado estable, con solamente una dirección principal. En función del tiempo, los susceptibles y los infectados acaban convergiendo exponencialmente al punto de equilibrio endémico según una dirección que converge a ∆I = {−[1 ⁄ √(1+μ)]−1} ∆S, donde ∆S y ∆S son la diferencia que tienen los susceptibles y los infectados, respectivamente, con sus valores endémicos.
Si R₀ > (2 ⁄ μ) [1+μ+√(1+μ)], el equilibrio endémico es nodo estable, con dos direcciones principales distintas. En función del tiempo, los susceptibles y los infectados acaban convergiendo exponencialmente al punto de equilibrio endémico.

La siguiente figura muestra un ejemplo del lugar geométrico de los autovalores del jacobiano en el equilibrio endémico cuando se varía R₀ con un valor de μ fijo:

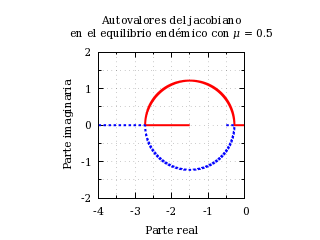
Lugar geométrico de los autovalores del jacobiano en el equilibrio endémico.

Echemos un vistazo a este lugar geométrico de los autovalores:

En el límite R₀ → 1, uno de los autovalores (el representado por la línea continua) se hace 0 y el otro (el representado por la línea de trazos) se hace −μ. Es el caso límite en el que no hay epidemia (el equilibrio endémico es el equilibrio libre de enfermedad).
Conforme crece el valor de R₀ por debajo de (2 ⁄ μ) [1+μ−√(1+μ)], ambos autovalores se acercan por el eje real a 1+μ−√(1+μ). El equilibrio endémico es un nodo atractor.
Con R₀ = (2 ⁄ μ) [1+μ−√(1+μ)], ambos autovalores coinciden en −[1+μ−√(1+μ)]. El equilibrio endémico en este punto es un nodo atractor degenerado.
Con (2 ⁄ μ) [1+μ−√(1+μ)] < R₀ < (2 ⁄ μ) [1+μ+√(1+μ)], los autovalores se mueven en el plano complejo por una circunferencia con centro en −(1+μ) y radio √(1+μ). El autovalor que partía de 0 (el de la línea continua en la figura) tiene parte imaginaria positiva y el autovalor que partía de −μ (el de la línea de trazos en la figura) tiene parte imaginaria negativa. La parte imaginaria tiene una magnitud máxima (igual al radio) cuando R₀ = 2 [(1+μ) ⁄ μ]. El equilibrio endémico es una espiral que converge más rápido conforme crece R₀ y que oscila a máxima frecuencia cuando R₀ = 2 [(1+μ) ⁄ μ.
Con R₀ = (2 ⁄ μ) [1+μ+√(1+μ)], ambos autovalores coinciden en −[1+μ−√(1+μ)]. El equilibrio endémico en este punto es un nodo atractor degenerado.
Con R₀ > (2 ⁄ μ) [1+μ+√(1+μ)], ambos autovalores vuelven a separarse por el eje real. El equilibrio endémico es un nodo atractor.
En el límite R₀ → ∞, el autovalor que partía de 0 (el de la línea continua en la figura) tiende a −(1+μ) y el que partía de −μ (el de la línea de trazos en la figura) tiende a −∞. El equilibrio endémico es un nodo atractor con una dirección infinitamente rápida.

Categorías: Matemáticas, Salud

Permalink: http://sgcg.es/articulos/2020/05/20/el-modelo-epidemiologico-sir-16/

Evolución del reparto izquierda/derecha en la Asamblea de Madrid

2020-05-18

Solamente por las risas, como ya hicimos con el Ayuntamiento de Madrid, vamos a ver cómo ha evolucionado el reparto de escaños de la Asamblea de Madrid en las burdas categorías de «izquierda» y «derecha» a lo largo de las últimas décadas. Igual que hicimos entonces, usaremos una torpe y arbitraria clasificación en la que consideraremos izquierdas los partidos normalmente clasificados como de izquierda y de centro izquierda (sopas de letras que incluyen variaciones de PSOE, PCE, CDS —que en 1987, la vez que consiguió representación con 17 escaños, estaba entre centro izquierda y centro derecha—, IU, Podemos y Más Madrid) y consideraremos derechas los partidos normalmente clasificados como de derecha y de centro derecha (sopas de letras que incluyen variaciones de AP, PP, UPyD, Ciudadanos y Vox). ¡Esta clasificación es discutible! Sea como sea, sigue una tabla con los resultados electorales:

Reparto en los grupos «de izquierdas» y «de derechas» de escaños en las elecciones a la Asamblea de Madrid a lo largo de las últimas décadas.

Año	Escaños «de izquierdas»	Escaños «de derechas»
1983	60	34
1987	64	32
1991	54	47
1995	49	54
1999	47	55
2003	56	55
2003	54	57
2007	53	67
2011	49	80
2015	64	65
2019	64	68

De forma gráfica, la evolución de la proporción de escaños queda como sigue:

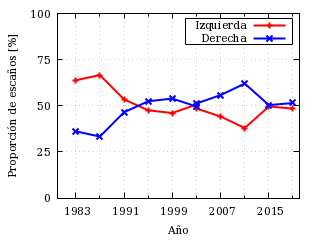
Evolución de la proporción de escaños en la Asamblea de Madrid entre «izquierdas» y «derechas».

Puede verse que la Comunidad de Madrid ni es abrumadoramente «roja» ni es abrumadoramente «facha».

Categorías: Madrid

Permalink: http://sgcg.es/articulos/2020/05/18/evolucion-del-reparto-izquierda-derecha-en-la-asamblea-de-madrid/

Gato con mascarilla

2020-05-15

Hoy parece un día excelente para dibujar gatitos, así que aquí tenéis uno:

Imagen PNG en paleta de 256 colores, 640 píxeles de ancho y 480 píxeles de alto, 25 kB.

Categorías: Dibujos

Permalink: http://sgcg.es/articulos/2020/05/15/gato-con-mascarilla/

El modelo epidemiológico SIR (15)

2020-05-12

El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:

Hoy investigaremos la naturaleza del equilibrio libre de enfermedad.

Recordemos que estamos estudiando los puntos fijos del siguiente sistema:

dS ⁄ dt = μ − (1+μ) R₀ S I − μ S;

dI ⁄ dt = (1+μ) R₀ S I − (1+μ) I.

Aparecen varios símbolos cuyo significado es el siguiente:

La variable dependiente S es la proporción susceptible de la población total.
La variable dependiente I es la proporción de la población infectada.
La variable independiente t es el tiempo hecho adimensional de forma que la población infectada pasa a ser población recuperada a un ritmo por unidad de tiempo adimensional igual a la propia población infectada. El primer artículo sobre los puntos fijos explica esto.
El símbolo μ denota tanto la natalidad como la mortalidad, que son iguales.
El símbolo R₀ es el ritmo reproductivo básico (los nuevos contagios que provoca el caso inicial).

El equilibrio libre de enfermedad es el siguiente punto:

S = 1, I = 0.

Las derivadas temporales se anulan en este punto. La matriz jacobiana tiene los autovalores:

autovalor −μ con dirección ∆I = 0 («horizontal»).
autovalor (1+μ) (R₀−1) con dirección ∆I = −[[(1+μ) R₀−1] ⁄ [(1+μ) R₀] ∆S («diagonal»).

Veamos qué sucede cuando μ > 0, que es la situación interesante con natalidad y mortalidad no nulas. En esta situación, el primer autovalor es siempre positivo independientemente de R₀, mientras que el segundo cambia de signo al variar R₀. En función de R₀, el punto de equilibrio es como sigue:

Cuando R₀ < 1, el punto de equilibrio es estable tanto en la dirección «horizontal» como en la dirección «diagonal»: se trata de un nodo atractor. Si se parte de una situación con unos pocos infectados, el sistema decae exponencialmente de vuelta al equilibrio libre de enfermedad y no es posible la epidemia. Tiene sentido: cada persona infectada provoca menos de un contagio antes de estar infectada, con lo que la enfermedad se extingue.
Cuando R₀ > 1, el punto de equilibrio es estable en la dirección «horizontal», pero inestable en la dirección «diagonal»: se trata de un punto silla. Además de esto, se ve que la dirección «diagonal», que es la inestable, se adentra en el dominio físico (S+I≤1, S≥0, I≥0) para cualquier R₀ > 1. Si se parte de una situación con unos pocos infectados, la epidemia crece inicialmente de forma exponencial. Tiene sentido: al menos al principio, cada persona infectada provoca más de un contagio antes de dejar de estar infectada, con lo que la epidemia se extiende.
Cuando R₀ = 1, el punto de equilibrio es estable en la dirección «horizontal» y linealmente neutro en la dirección «diagonal». Si no nos limitamos al desarrollo lineal, vemos que el punto es completamente estable desde dentro del dominio físico: no es posible la epidemia. Si se parte de una situación con unos pocos infectados, el sistema converge muy lentamente al equilibrio libre de enfermedad (la distancia a este punto tiende a ser proporcionalmente inversa al tiempo transcurrido debido a que el término no nulo es cuadrático).

Categorías: Matemáticas, Salud

Permalink: http://sgcg.es/articulos/2020/05/12/el-modelo-epidemiologico-sir-15/

El modelo epidemiológico SIR (14)

2020-05-09

El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:

Hoy identificaremos los puntos fijos o puntos de equilibrio del sistema referido a los susceptibles y los infectados.

Recordemos que el modelo sigue a lo largo del tiempo t la evolución de la población susceptible S(t), la población infectada I(t) y la población recuperada (inmune) R(t) mediante el siguiente sistema dinámico:

dS ⁄ dt = μ N − β S I ⁄ N − μ S;

dI ⁄ dt = β S I ⁄ N − γ I − μ I;

dR ⁄ dt = γ I − μ R.

Aparecen varios símbolos cuyo significado es el siguiente:

El símbolo N denota la población total, S + I + R, que se mantiene constante. Como anteriormente, como la población es constante, es muy cómodo tomar N = 1 y trabajar con proporciones de la población total.
El símbolo μ denota tanto la natalidad como la mortalidad, que son iguales.
El símbolo β denota la tasa de infección. Vimos que está relacionado con el ritmo reproductivo básico R₀ (los nuevos contagios que provoca el caso inicial) mediante la relación R₀ = (γ+μ) β.
El símbolo γ denota la tasa de recuperación de los infectados. En anteriores artículos era el inverso del tiempo infeccioso promedio, pero ahora las defunciones complican un poco la interpretación.

Para estudiar cualitativamente cómo se comporta el modelo en función de los parámetros, podemos tomar N como unidad de población (de manera N = 1 en las ecuaciones y trabajamos con proporciones sobre la población total como en los primeros artículos) y γ⁻¹ como unidad de tiempo (de manera que γ = 1 en las ecuaciones). Este escalado de los parámetros es razonable en todas las situaciones físicamente posibles salvo en el caso degenerado de una enfermedad sin posible recuperación (γ = 0, que sería el modelo SI, sin estado R). Las ecuaciones quedan un poco más sencillas:

dS ⁄ dt = μ − (1+μ) R₀ S I − μ S;

dI ⁄ dt = (1+μ) R₀ S I − (1+μ) I.

Como S + I + R = 1, el modelo es realmente bidimensional y no tridimensional, así que hemos obviado la variable R por ser redundante.

Las ecuaciones tienen dos puntos fijos en los que ni S ni I varían:

S = 1, I = 0;

S = 1 ⁄ R₀, I = [μ ⁄ (1+μ)] [(R₀−1) ⁄ R₀].

El primer punto fijo es el equilibrio libre de enfermedad: toda la población permanece infectada. El segundo punto fijo es el equilibrio endémico: los nuevos susceptibles que tras nacer se infectan equilibran las muertes y recuperaciones. En los próximos artículos exploraremos la naturaleza de estos puntos fijos; hoy es suficiente localizarlos.

El equilibrio libre de enfermedad no se mueve con los parámetros. El equilibrio endémico sí se mueve, pero es evidente que lo hace en la siguiente recta:

I = [μ ⁄ (1+μ)] (1−S).

El equilibrio endémico solamente tiene sentido físico cuando el ritmo reproductivo es igual o mayor que la unidad. Los susceptibles parten de ser toda la población a anularse cuando el ritmo reproductivo básico tiende a infinito. Los infectados parten de ser nulos a ser [μ ⁄ (1+μ)] cuando el ritmo reproductivo básico tiende a infinito.

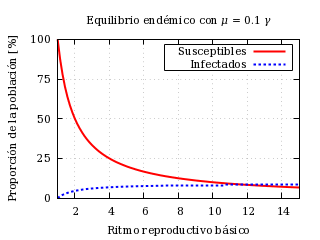
Equilibrio endémico frente al ritmo reproductivo básico para cierto valor de la tasa de natalidad y mortalidad.

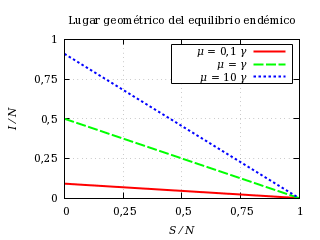
Lugar geométrico del equilibrio endémico para distintos valores de la tasa de natalidad y mortalidad.

Categorías: Matemáticas, Salud

Permalink: http://sgcg.es/articulos/2020/05/09/el-modelo-epidemiologico-sir-14/

El modelo epidemiológico SIR (13)

2020-05-04

El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:

Hoy veremos cómo extraer el ritmo reproductivo básico del modelo con natalidad y mortalidad en equilibrio.

Recordemos que el modelo sigue a lo largo del tiempo t la evolución de la población susceptible S(t), la población infectada I(t) y la población recuperada (inmune) R(t) mediante el siguiente sistema dinámico:

dS ⁄ dt = μ N − β S I ⁄ N − μ S;

dI ⁄ dt = β S I ⁄ N − γ I − μ I;

dR ⁄ dt = γ I − μ R.

Aparecen varios símbolos cuyo significado es el siguiente:

El símbolo N denota la población total, S + I + R, que se mantiene constante. Como anteriormente, como la población es constante, es muy cómodo tomar N = 1 y trabajar con proporciones de la población total.
El símbolo μ denota tanto la natalidad como la mortalidad, que son iguales.
El símbolo β denota la tasa de infección. En anteriores artículos era el ritmo reproductivo básico dividido entre el tiempo infeccioso promedio, pero ahora los nacimientos y las defunciones complican un poco la interpretación.
El símbolo γ denota la tasa de recuperación de los infectados. En anteriores artículos era el inverso del tiempo infeccioso promedio, pero ahora las defunciones complican un poco la interpretación.

El ritmo reproductivo básico es el número de contagios que genera el primer sujeto infectado. En este modelo, hablar del primer sujeto infectado es lo mismo que hablar de S(0) ≅ N, I(0) ≪ N, R(0) = 0. Linealicemos el comportamiento de los infectados alrededor de este estado inicial:

dI ⁄ dt ≅ β I − γ I − μ I.

Hagamos un seguimiento exclusivo del primer infectado. Para ello, tenemos que ignorar el término de nuevos contagios β I. Con abuso de notación, nuestro «paciente cero» evoluciona cumpliendo la ley siguiente:

dI ⁄ dt ≅ −γ I − μ I.

Con esta ecuación, la evolución a partir de I(0) es como sigue:

I(t) ≅ I(0) e^{−(γ+μ) t}.

Así decae esta visión del caso inicial que tiene el modelo. Esta infección inicial genera β I nuevos contagios por unidad de tiempo, con lo que los nuevos contagios generados por la infección inicial son

R₀ I(0) = ∫_0≤t<∞β I(t) dt = [β ⁄ (γ+μ)] I(0).

Por lo tanto, el ritmo reproductivo básico es

R₀ = β ⁄ (γ+μ).

La generalización de este razonamiento es el método de la matriz de próxima generación, por cierto, que sirve para asignar un ritmo reproductivo básico a modelos compartimentales de forma muy general.

Categorías: Matemáticas, Salud

Permalink: http://sgcg.es/articulos/2020/05/04/el-modelo-epidemiologico-sir-13/

SGCG

Mayo de 2020

Calendario de artículos de de 2020

Cardo

Boeing anuncia más de 12000 despidos

El modelo epidemiológico SIR (18)

Posibles comportamientos a largo plazo

Las órbitas cerradas no son posibles

Las soluciones acaban convergiendo a puntos fijos

El modelo epidemiológico SIR (17)

Los susceptibles no pueden hacerse negativos

Los infectados no pueden hacerse negativos

La suma de susceptibles e infectados nunca puede superar a la población total

Conclusión: las soluciones están confinadas en la región con sentido físico

Liquen

El modelo epidemiológico SIR (16)

Evolución del reparto izquierda/derecha en la Asamblea de Madrid

Gato con mascarilla

El modelo epidemiológico SIR (15)

El modelo epidemiológico SIR (14)

El modelo epidemiológico SIR (13)

Categorías

Calendario de artículos de de 2024

Archivo

Suscripción