El modelo epidemiológico SIR (19)

2020-06-13

El modelo SIR es un modelo muy sencillo del comportamiento de una epidemia a lo largo del tiempo. Tras explicar algunas características del modelo, vimos:

cómo simplificar el modelo para analizar el comienzo de la propagación de una nueva epidemia;
el comportamiento de la proporción de infectados en esta fase inicial;
cómo relacionar las variables sin necesidad de integrar en el tiempo;
cómo calcular el máximo número de infectados simultáneos;
cómo calcular el resultado final de la epidemia;
cómo se comporta la epidemia en el entorno del máximo de infectados simultáneos;
cómo varían los infectados cerca del final de la epidemia;
cómo se relacionan la fase de crecimiento exponencial inicial de la epidemia y la fase de decrecimiento exponencial final de la epidemia;
qué condición es necesaria para la inmunidad de grupo;
cómo queda modificado el modelo si en vez de trabajar con proporciones sobre la población total, trabajamos con números absolutos de individuos;
cómo plantear el modelo cuando hay nacimientos y defunciones, pero la población total se mantiene estable;
cómo extraer el ritmo reproductivo básico del modelo con natalidad y mortalidad en equilibrio;
los puntos fijos o puntos de equilibrio del sistema referido a los susceptibles y los infectados;
la naturaleza del punto de equilibrio libre de enfermedad;
la naturaleza del equilibrio endémico;
cómo las soluciones se mantienen confinadas en el conjunto de valores que tiene sentido físico;
cómo las soluciones siempre convergen a algún punto de equilibrio (bien el equilibrio endémico, bien el equilibrio libre de enfermedad).

Hoy vamos a ilustrar el comportamiento del sistema para varios conjuntos de parámetros.

Recordemos que estamos estudiando el siguiente sistema autónomo:

dS ⁄ dt = μ − (1+μ) R₀ S I − μ S;

dI ⁄ dt = (1+μ) R₀ S I − (1+μ) I.

Aparecen varios símbolos cuyo significado es el siguiente:

La variable dependiente S es la proporción susceptible de la población total.
La variable dependiente I es la proporción de la población infectada.
La variable independiente t es el tiempo hecho adimensional de forma que la población infectada pasa a ser población recuperada a un ritmo por unidad de tiempo adimensional igual a la propia población infectada. El primer artículo sobre los puntos fijos explica esto.
El símbolo μ denota tanto la natalidad como la mortalidad, que son iguales. Este número es nulo en el caso en el que no hay nacimientos ni muertes (o cuando se producen a un ritmo tan lento que es legítimo despreciar su efecto) y es positivo en el caso más general.
El símbolo R₀ es el ritmo reproductivo básico (los nuevos contagios que provoca el caso inicial). Este número es nulo en el caso trivial de una enfermedad que no se contagia y positivo en el caso general de las enfermedades contagiosas.

Veamos unos cuantos retratos de fase, que muestran la forma de las trayectorias del sistema en el plano S, I.

En los retratos de fase siguientes, el equilibrio libre de enfermedad aparece como un símbolo vacío en S = 1, I = 0; el equilibrio endémico aparece como un símbolo relleno, las trayectorias son líneas continuas y las flechas indican la dirección del campo de velocidades dS ⁄ dt, dI ⁄ dt.

Las epidemias son débiles cuando 1 < R₀ < (2 ⁄ μ) [1+μ−√(1+μ)] y el equilibrio endémico es un nodo estable; son moderadas cuando (2 ⁄ μ) [1+μ−√(1+μ)] < R₀ < (2 ⁄ μ) [1+μ+√(1+μ)] y el equilibrio endémico es una espiral atractora; y son fuertes cuando R₀ > (2 ⁄ μ) [1+μ+√(1+μ)] y el equilibrio endémico vuelve a ser un nodo estable.

Recordemos que estábamos expresando el tiempo en unidades tales que el ritmo de recuperación es unitario. La natalidad es baja cuando el ritmo de natalidad es muy inferior al ritmo de recuperación (μ ≪ 1) y la epidemia se comporta como si no hubiera natalidad durante mucho tiempo antes de que se note el efecto de la natalidad; la natalidad es moderada cuando el ritmo de natalidad es próximo al ritmo de recuperación (μ ≅ 1) y los efectos de natalidad y recuperación son comparables; y la natalidad es alta cuando el ritmo de natalidad es muy superior al ritmo de recuperación (μ ≫ 1) y el efecto de recuperación es despreciable.

Epidemia con natalidad nula

Con una natalidad nula (μ = 0) y una epidemia cualquiera (R₀ > 1), no existe el equilibrio endémico y todas las trayectorias acaban en algún punto del eje I = 0.

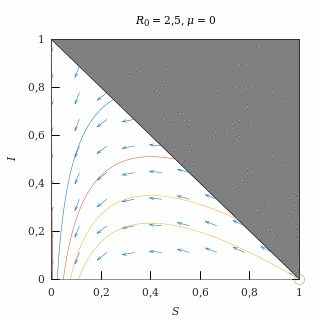
Retrato de fase de una epidemia con natalidad nula.

Epidemia débil con natalidad baja

Con una natalidad baja (μ = 0,05) y una epidemia débil (R₀ = 1,01), el equilibrio endémico es un nodo estable, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo exponencialmente al equilibrio endémico.

Como la natalidad es baja, las trayectorias permanecen durante mucho tiempo muy similares a las que se producen sin natalidad y, finalmente, quiebran para dirigirse hacia el equilibrio endémico.

El equilibrio endémico está muy próximo al equilibrio libre de enfermedad debido a que la epidemia es débil.

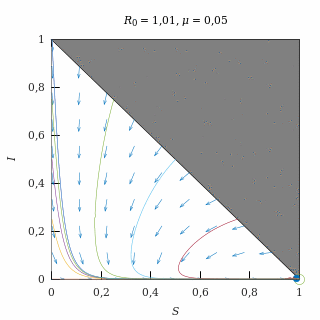
Retrato de fase de una epidemia débil con natalidad baja.

Epidemia moderada con natalidad baja

Con una natalidad baja (μ = 0,05) y una epidemia moderada (R₀ = 2,5), el equilibrio endémico es una espiral atractora, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo oscilatoriamente al equilibrio endémico.

Como la natalidad es baja, las trayectorias permanecen durante mucho tiempo muy similares a las que se producen sin natalidad y, finalmente, quiebran para dirigirse hacia el equilibrio endémico.

El equilibrio endémico está lejos del equilibrio libre de enfermedad debido a que la epidemia es moderada.

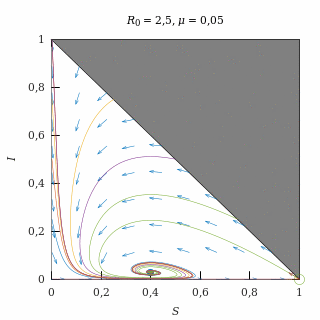
Retrato de fase de una epidemia moderada con natalidad baja.

Epidemia fuerte con natalidad baja

Con una natalidad baja (μ = 0,05) y una epidemia fuerte (R₀ = 100), el equilibrio endémico es una espiral atractora, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo oscilatoriamente al equilibrio endémico.

Como la natalidad es baja, las trayectorias permanecen durante mucho tiempo muy similares a las que se producen sin natalidad y, finalmente, quiebran para dirigirse hacia el equilibrio endémico.

El equilibrio endémico deja muy pocos susceptibles debido a que la epidemia es fuerte.

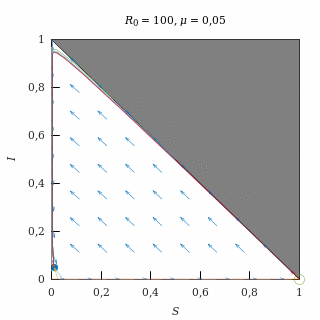
Retrato de fase de una epidemia fuerte con natalidad baja.

Epidemia débil con natalidad moderada

Con una natalidad moderada (μ = 1) y una epidemia débil (R₀ = 1,15), el equilibrio endémico es un nodo estable, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo exponencialmente al equilibrio endémico.

Como la natalidad es moderada, las trayectorias tienen poco que ver con las que se producían sin natalidad.

El equilibrio endémico está muy próximo al equilibrio libre de enfermedad debido a que la epidemia es débil.

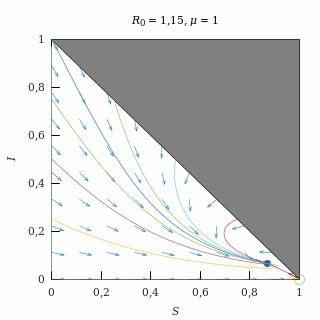
Retrato de fase de una epidemia débil con natalidad moderada.

Epidemia moderada con natalidad moderada

Con una natalidad moderada (μ = 1) y una epidemia moderada (R₀ = 4), el equilibrio endémico es una espiral atractora, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo oscilatoriamente al equilibrio endémico.

Como la natalidad es moderada, las trayectorias tienen poco que ver con las que se producían sin natalidad.

El equilibrio endémico está lejos del equilibrio libre de enfermedad debido a que la epidemia es moderada.

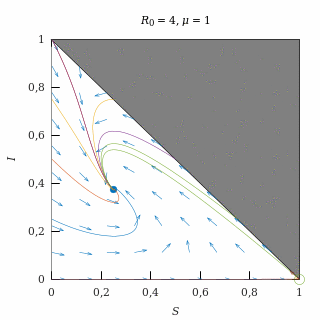
Retrato de fase de una epidemia moderada con natalidad moderada.

Epidemia fuerte con natalidad moderada

Con una natalidad moderada (μ = 1) y una epidemia fuerte (R₀ = 10), el equilibrio endémico es un nodo estable, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo exponencialmente al equilibrio endémico.

Como la natalidad es moderada, las trayectorias tienen poco que ver con las que se producían sin natalidad.

El equilibrio endémico deja muy pocos susceptibles debido a que la epidemia es fuerte.

Retrato de fase de una epidemia fuerte con natalidad moderada.

Epidemia débil con natalidad alta

Con una natalidad alta (μ = 10) y una epidemia débil (R₀ = 1,25), el equilibrio endémico es un nodo estable, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo exponencialmente al equilibrio endémico.

Como la natalidad es alta, las trayectorias tienden a vivir en el eje S + I = 1, que es el que corresponde a una situación en la que no hay tasa de recuperación.

El equilibrio endémico está muy próximo al equilibrio libre de enfermedad debido a que la epidemia es débil.

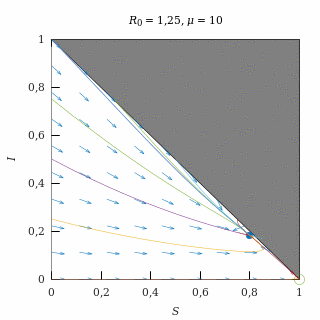
Retrato de fase de una epidemia débil con natalidad alta.

Epidemia moderada con natalidad alta

Con una natalidad alta (μ = 10) y una epidemia moderada (R₀ = 2), el equilibrio endémico es una espiral atractora, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo oscilatoriamente al equilibrio endémico.

Como la natalidad es alta, las trayectorias tienden a vivir en el eje S + I = 1, que es el que corresponde a una situación en la que no hay tasa de recuperación.

El equilibrio endémico está lejos del equilibrio libre de enfermedad debido a que la epidemia es moderada.

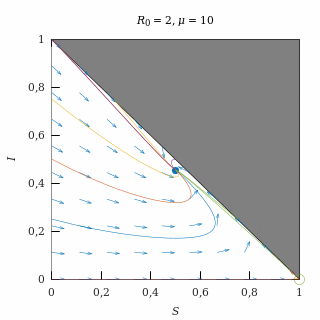
Retrato de fase de una epidemia moderada con natalidad moderada.

Epidemia fuerte con natalidad alta

Con una natalidad elevada (μ = 10) y una epidemia fuerte (R₀ = 3,5), el equilibrio endémico es un nodo estable, así que casi todas las trayectorias (salvo las del eje I = 0) acaban convergiendo exponencialmente al equilibrio endémico.

Como la natalidad es alta, las trayectorias tienden a vivir en el eje S + I = 1, que es el que corresponde a una situación en la que no hay tasa de recuperación.

El equilibrio endémico deja muy pocos susceptibles debido a que la epidemia es fuerte.

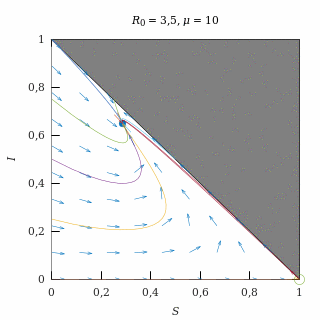
Retrato de fase de una epidemia fuerte con natalidad elevada.